51nod 1536不一样的猜数游戏 思路：O（n）素数筛选法。同Codeforces 576A Vasya and Petya's Game。

废话不多说，先上题目。

51nod

 

Codeforces

 

两个其实是一个意思，看51nod题目就讲的很清楚了，题意不再赘述。

直接讲我的分析过程：刚开始拿到手有点蒙蔽，看起来很难，然后。。。。。。然后我就开始一顿胡蒙，各种举例子、找规律下面为我取n = 10的过程。

 

1.首先1肯定不用取。因为它太特殊了，如果 取它的话，只能判断是不是1，因为所有数都是1的倍数；反之其他所有情况排除了就选它，不用浪费次数来取它。

2.素数肯定是要取的。因为。。。。。。因为这题一看就是考素数的题。

3.以10为例，如果是2，3的倍数，则为6。如果是2，5的倍数则为10。如果不是2的倍数，是5的倍数则为5。如果是7的倍数则为7。现在我们根据2，3，5，7这4个素数选出了6，10，5，7这4个数。肯定还要再加数，怎么加？

4.如果加一个数能多判断更多的数最好了，先考虑3，3的倍数有3、6和9，6我们用2、3组合判断过了，3和9能怎么判断？肯定不能不选3而选9用排除法，因为1已经用了排除法，排除法只能用一次。因为要判断所有数字，想要判断3和9必须要同时取3和9，这样只多取了一个9我们就多判断了两个数字。现在我们能判断6、10、5、7、3、9这6个数字了。

5.再看2，2的倍数有2、4、6、8、10。6和10我们已经用2、3和2、5组合判断了，我们观察剩余的数字还有2、4、8，我尼玛？什么情况，如果刚刚的3和9是巧合的话，这里的2、4、8还是巧合？现在我们取中2、4、8三个数就可以判断这3个数了。我们判断出了9个数6、10、5、7、3、9、2、4、8，然后1用排除法，所以我们判断出了这10个数了。

这里我们观察到我们选出的都是素数的次方（小于n）。以10为例，2，4，8（2的次方）；3，9（3的次方）；5（5的次方）；7（7的次方）。然后多试几例，发现就是这个规律。

现在我们有两条路可走：

1. 找出所有的素数和它的次方（小于n），顺带用一个count计数。
2. 找出所有不取的数计数count，然后用n减去这个count。即为任意找出两个素数a、b。排除所有a的次方 乘 b的次方。什么？为什么排除它们？想一想第一条路的补集不就是它们吗？

然后分析，发现第一条路只用找出素数及其次方，第二条路要在第一条路的基础上做更多工作，所以果断选择第一条路。

下面是代码了：

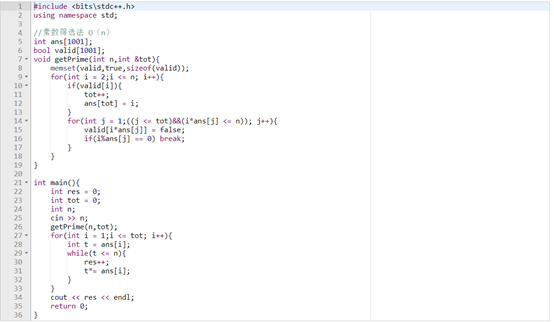
再加点注释：

#include <bitsstdc++.h>
using namespace std;

//素数筛选法 O（n） ,见那本小红书（ACM国际大学生程序设计竞赛-算法与实现） 
int ans[1001];  //存入所有素数。 
bool valid[1001];  //判断第i个是不是素数。 
void getPrime(int n,int &tot){
    memset(valid,true,sizeof(valid));
    for(int i = 2;i <= n; i++){
        if(valid[i]){
            tot++;
            ans[tot] = i;
        }
        for(int j = 1;((j <= tot)&&(i*ans[j] <= n)); j++){
            valid[i*ans[j]] = false;
            if(i%ans[j] == 0) break;
        }
    }
}

int main(){
    int n;
    cin >> n;
    int res = 0;   // 素数及其次方的数量 
    int tot = 0;  // 小于等于n的素数的数量 
    getPrime(n,tot);  //筛选出素数 
    
    for(int i = 1;i <= tot; i++){  //遍历范围内素数，找出其次方 
        int t = ans[i];
        while(t <= n){
            res++;
            t*= ans[i];
        }
    }
    
    cout << res << endl;
    return 0;
}