二叉树的操作

        先使用先序的方法建立一棵二叉树，然后分别使用递归与非递归的方法实现前序、中序、后序遍历二叉树，并使用了两种方法来进行层次遍历二叉树，一种方法就是使用STL中的queue，另外一种方法就是定义了一个数组队列，分别使用了front和rear两个数组的下标来表示入队与出队，还有两个操作就是求二叉树的深度、结点数。。。

#include "iostream"
#include "queue"
#include "stack"
using namespace std;

//二叉树结点的描述
typedef struct BiTNode
{
    char data;
    struct BiTNode *lchild, *rchild;      //左右孩子
}BiTNode,*BiTree;

//按先序遍历创建二叉树
//BiTree *CreateBiTree()     //返回结点指针类型
//void CreateBiTree(BiTree &root)      //引用类型的参数
void CreateBiTree(BiTNode **root)    //二级指针作为函数参数
{
    char ch; //要插入的数据
    scanf("\n%c", &ch);
    //cin>>ch;
    if(ch=='#')
        *root = NULL;
    else
    {
        *root = (BiTNode *)malloc(sizeof(BiTNode));
        (*root)->data = ch;
        printf("请输入%c的左孩子：",ch);
        CreateBiTree(&((*root)->lchild));
        printf("请输入%c的右孩子：",ch);
        CreateBiTree(&((*root)->rchild));
    }
}

//前序遍历的算法程序
void PreOrder(BiTNode *root)
{
    if(root==NULL)
        return ;
    printf("%c ", root->data); //输出数据
    PreOrder(root->lchild); //递归调用，前序遍历左子树
    PreOrder(root->rchild); //递归调用，前序遍历右子树
}

//中序遍历的算法程序
void InOrder(BiTNode *root)
{
    if(root==NULL)
        return ;
    InOrder(root->lchild); //递归调用，前序遍历左子树
    printf("%c ", root->data); //输出数据
    InOrder(root->rchild); //递归调用，前序遍历右子树
}

//后序遍历的算法程序
void PostOrder(BiTNode *root)
{
    if(root==NULL)
        return ;
    PostOrder(root->lchild); //递归调用，前序遍历左子树
    PostOrder(root->rchild); //递归调用，前序遍历右子树
    printf("%c ", root->data); //输出数据
}

void PreOrder_Nonrecursive(BiTree T)  //先序遍历的非递归
{
    stack<BiTree> S;
    BiTree p;
    S.push(T);  //根指针进栈
    while(!S.empty())  //栈空时结束
    {
        while((p=S.top()) && p)
        {
            cout<<p->data<<"  ";
            S.push(p->lchild);
        }   //向左走到尽头
        S.pop();  //弹出堆栈
        if(!S.empty())
        {
            p=S.top();
            S.pop();
            S.push(p->rchild);    //向右走一步
        }
    }
}
void InOrderTraverse(BiTree T)   //中序遍历的非递归
{
    stack<BiTree> S;
    BiTree p;
    S.push(T);   //根指针进栈
    while(!S.empty())
    {
        while((p=S.top()) && p)
            S.push(p->lchild);    //向左走到尽头
        S.pop();    //空指针退栈
        if(!S.empty())
        {
            p=S.top();
            S.pop();
            cout<<p->data<<"  ";
            S.push(p->rchild);
        }
    }
}

void PostOrder_Nonrecursive(BiTree T)  //后序遍历的非递归
{
    stack<BiTree> S;
    BiTree p=T,q=NULL;
    while(p!=NULL || !S.empty())  //栈空时结束
    {
        while(p!=NULL)
        {
            S.push(p);
            p=p->lchild;
        }
        p=S.top();
        if(p->rchild==NULL || p->rchild==q)
        {
            cout<<p->data<<"  ";
            q=S.top();
            S.pop();
            p=NULL;
        }
        else
            p=p->rchild;
    }
}
int visit(BiTree T)
{
    if(T)
    {
        printf("%c ",T->data);
        return 1;
    }
    else
        return 0;
}

void LeverTraverse(BiTree T)   //方法一、非递归层次遍历二叉树
{
    queue <BiTree> Q;
    BiTree p;
    p = T;
    if(visit(p)==1)
        Q.push(p);
    while(!Q.empty())
    {
        p = Q.front();
        Q.pop();
        if(visit(p->lchild) == 1)
            Q.push(p->lchild);
        if(visit(p->rchild) == 1)
            Q.push(p->rchild);
    }
}
void LevelOrder(BiTree BT)     //方法二、非递归层次遍历二叉树
{
    BiTNode *queue[10];//定义队列有十个空间
    if (BT==NULL)
        return;
    int front,rear;
    front=rear=0;
    queue[rear++]=BT;
    while(front!=rear)//如果队尾指针不等于对头指针时
    {
        cout<<queue[front]->data<<"  ";  //输出遍历结果
        if(queue[front]->lchild!=NULL)  //将队首结点的左孩子指针入队列
        {
            queue[rear]=queue[front]->lchild;
            rear++;    //队尾指针后移一位
        }
        if(queue[front]->rchild!=NULL)
        {
            queue[rear]=queue[front]->rchild;    //将队首结点的右孩子指针入队列
            rear++;   //队尾指针后移一位
        }
        front++;    //对头指针后移一位
    }
}

int depth(BiTNode *T)   //树的深度
{
    if(!T)
        return 0;
    int d1,d2;
    d1=depth(T->lchild);
    d2=depth(T->rchild);
    return (d1>d2?d1:d2)+1;
    //return (depth(T->lchild)>depth(T->rchild)?depth(T->lchild):depth(T->rchild))+1;
}
int CountNode(BiTNode *T)
{
    if(T == NULL)
        return 0;
    return 1+CountNode(T->lchild)+CountNode(T->rchild);
}

int main(void)
{
    BiTNode *root=NULL; //定义一个根结点
    int flag=1,k;
    printf("                     本程序实现二叉树的基本操作。\n");
    printf("可以进行建立二叉树，递归先序、中序、后序遍历，非递归先序、中序遍历及非递归层序遍历等操作。\n");

    while(flag)
    {
        printf("\n");
        printf("|--------------------------------------------------------------|\n");
        printf("|                    二叉树的基本操作如下:                     |\n");
        printf("|                        0.创建二叉树                          |\n");
        printf("|                        1.递归先序遍历                        |\n");
        printf("|                        2.递归中序遍历                        |\n");
        printf("|                        3.递归后序遍历                        |\n");
        printf("|                        4.非递归先序遍历                      |\n");
        printf("|                        5.非递归中序遍历                      |\n");
        printf("|                        6.非递归后序遍历                      |\n");
        printf("|                        7.非递归层序遍历                      |\n");
        printf("|                        8.二叉树的深度                        |\n");
        printf("|                        9.二叉树的结点个数                    |\n");
        printf("|                        10.退出程序                            |\n");
        printf("|--------------------------------------------------------------|\n");
        printf("                        请选择功能：");
        scanf("%d",&k);
        switch(k)
        {
        case 0:
            printf("请建立二叉树并输入二叉树的根节点：");
            CreateBiTree(&root);
            break;
        case 1:
            if(root)
            {
                printf("递归先序遍历二叉树的结果为：");
                PreOrder(root);
                printf("\n");
            }
            else
                printf("          二叉树为空！\n");
            break;
        case 2:
            if(root)
            {
                printf("递归中序遍历二叉树的结果为：");
                InOrder(root);
                printf("\n");
            }
            else
                printf("          二叉树为空！\n");
            break;
        case 3:
            if(root)
            {
                printf("递归后序遍历二叉树的结果为：");
                PostOrder(root);
                printf("\n");
            }
            else
                printf("          二叉树为空！\n");
            break;
        case 4:
            if(root)
            {
                printf("非递归先序遍历二叉树：");
                PreOrder_Nonrecursive(root);
                printf("\n");
            }
            else
                printf("          二叉树为空！\n");
            break;
        case 5:
            if(root)
            {
                printf("非递归中序遍历二叉树：");
                InOrderTraverse(root);
                printf("\n");
            }
            else
                printf("          二叉树为空！\n");
            break;
        case 6:
            if(root)
            {
                printf("非递归后序遍历二叉树：");
                PostOrder_Nonrecursive(root);
                printf("\n");
            }
            else
                printf("          二叉树为空！\n");
            break;
        case 7:
            if(root)
            {
                printf("非递归层序遍历二叉树：");
                //LeverTraverse(root);
                LevelOrder(root);
                printf("\n");
            }
            else
                printf("          二叉树为空！\n");
            break;
        case 8:
            if(root)
                printf("这棵二叉树的深度为：%d\n",depth(root));
            else
                printf("          二叉树为空！\n");
            break;
        case 9:
            if(root)
                printf("这棵二叉树的结点个数为：%d\n",CountNode(root));
            else
                printf("          二叉树为空！\n");
            break;
        default:
            flag=0;
            printf("程序运行结束，按任意键退出！\n");
        }
    }
    system("pause");
    return 0;
}

运行效果图如下：

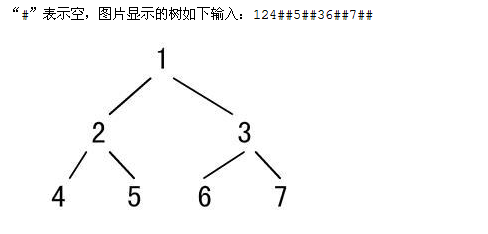
分别输入：

1

2

4

#

#

5

#

#

3

6

#

#

7

#

# 

就可以构造如下图所示的二叉树了。。

后序遍历非递归的另外一种写法：

/*
后序遍历由于遍历父节点是在遍历子节点之后，而且左节点和右节点遍历后的行为不一样，
所以需要用变量来记录前一次访问的节点，根据前一次节点和现在的节点的关系来确定具体执行什么操作
*/
void Postorder(BiTree T)
{
    if(T == NULL)
        return ;
    stack<BiTree> s;
    BiTree prev = NULL , curr = NULL;
    s.push(T);
    while(!s.empty())
    {
        curr = s.top();
        if(prev == NULL  || prev->lchild == curr || prev->rchild == curr)
        {
            if(curr->lchild != NULL)
                s.push(curr->lchild);
            else if(curr->rchild != NULL)
                s.push(curr->rchild);
        }
        else if(curr->lchild == prev)
        {
            if(curr->rchild != NULL)
                s.push(curr->rchild);
        }
        else
        {
            cout<<curr->data;
            s.pop();
        }
        prev = curr;
    }
}

输入二叉树中的两个节点，输出这两个结点在数中最低的共同父节点。
思路：遍历二叉树，找到一条从根节点开始到目的节点的路径，然后在两条路径上查找共同的父节点。

// 得到一条从根节点开始到目的节点的路径
bool GetNodePath(TreeNode *pRoot , TreeNode *pNode , vector<TreeNode *> &path)
{
    if(pRoot == NULL)
        return false;
    if(pRoot == pNode)
        return true;
    else if(GetNodePath(pRoot->lchild , pNode , path) )
    {
        path.push_back(pRoot->lchild);
        return true;
    }
    else if(GetNodePath(pRoot->rchild , pNode , path) )
    {
        path.push_back(pRoot->rchild);
        return true;
    }
    return false;
}
TreeNode *GetLastCommonNode(const vector<TreeNode *> &path1 , const vector<TreeNode *> &path2)
{
    vector<TreeNode *>::const_iterator iter1 = path1.begin();
    vector<TreeNode *>::const_iterator iter2 = path2.begin();
    TreeNode *pLast;
    while(iter1 != path1.end() && iter2 != path2.end() )
    {
        if(*iter1 == *iter2)
            pLast = *iter1;
        else
            break;
        iter1++;
        iter2++;
    }
    return pLast;
}
TreeNode *GetLastCommonParent(TreeNode *pRoot , TreeNode *pNode1 , TreeNode *pNode2)
{
    if(pRoot == NULL || pNode1 == NULL || pNode2 == NULL)
        return  NULL;
    vector<TreeNode *> path1;
    GetNodePath(pRoot , pNode1 , path1);

    vector<TreeNode *> path2;
    GetNodePath(pRoot , pNode2 , path2);
    return GetLastCommonNode(path1 , path2);
}