信息是一个很抽象的东西,吃苹果的概率是二分之一,吃香蕉的概率是二分之一,这里面包含了多少信息量,由于信息很抽象,无法直观的量化。
信息熵原先是热力学中的名词,原先含义是表示分子状态的混乱程度。
香农引用了信息熵概念,因此,便有了信息论这一门学科,信息熵表示一个事件或者变量的混乱程度(也可称为一个事件的不确定性),将信息变成可以量化的变量。
综上所述,信息熵是信息论中用于度量信息量的一个概念。一个系统越是有序,信息熵就越低;反之,一个系统越是混乱,信息熵就越高。所以,信息熵也可以说是系统有序化程度的一个度量。高信息度的信息熵是很低的,低信息度的熵则高。具体说来, 凡是随机事件导致的变化,都可以用信息熵的改变量这个统一的标尺来度量。
换一种说法:信我们可以吧信息熵理解为一个随机变量出现的期望值,也就是说信息熵越大,该随机变量会有更多的形式。信息熵衡量了一个系统的复杂度,比如当我们想要比较两门课哪个更复杂的时候,信息熵就可以为我们作定量的比较,信息熵大的就说明那门课的信息量大,更加复杂。
举个例子:里约奥运会,女子自由泳决赛有两个国家,美国和中国,中国获胜的概率是80%,美国获胜的概率是20%。则谁获得冠军的信息熵=- 0.8 * log2 0.8 - 0.2 * log2 0.2 = 0.257 + 0.464 = 0.721。中国获胜的几率越高,计算出的熵就越小,即越是确定的情况,不确定性越小,信息熵越少。如果中国100%夺冠,那么熵是0,相当于没有任何信息。当两队几率都是50%最难判断,所熵达到最大值1。
信息熵有很多定义,但都类似,简单来说,就是信息熵可以衡量事物的不确定性,这个事物不确定性越大,信息熵也越大就是信息熵可以衡量事物的不确定性,这个事物不确定性越大,信息熵也越大。
熵的一般公式是:
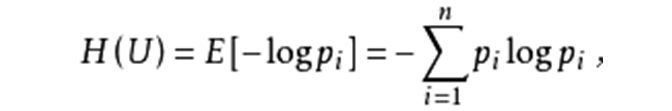
也可以写成:
借用一本书上的例子
32只球队共有32种夺冠的可能性,用多少信息量才能包括这32个结果?按照计算机的二进制(只有1和0)表示法,我们知道2^5=32 ,也就是需要5符号的组合结果就可以完全表示这32个变化,而这里的符号通常称之为比特。既然是这样,那么当一件事的结果越不确定时,也就是变化情况越多时,那么你若想涵盖所有结果,所需要的比特就要越多,也就是,你要付出的信息量越大,也即信息熵越大。当然,每个变化出现的概率不同,因而在香农的公式中才会用概率,所以信息熵算的是了解这件事所付出的平均信息量。比如这个例子里假设32只球队夺冠可能性相同,即Pi=1/32 ,那么按照香农公式计算:
entropy(P1,P2,...,P32)=-(1/32)log(1/32)-(1/32)log(1/32)......-(1/32)log(1/32)=5/32+5/32...+5/32=(5*32)/32 =5
信息熵同样可以用作数据挖掘中(如聚类分析过程)