数据结构和算法

一 数据结构：

常见的数据结构：

① 数组
② 链表
③ 树
④ 图

数据结构：

个体 + 个体的关系

数据结构和算法的定义：

我们如何把现实中大量而且非常复杂的问题以特定的数据类型（个体）和特定的存储结构（个体的关系）保存到相应的主存储（内存）中。

以及在此基础上为实现某个功能而执行的相应操作，这个相应的操作也叫作算法。

1 、连续存储：数组、列表

① 数组：申请一块连续的内存空间

优点：存取速度快。（因为连续的不需要再进行查找）

缺点：插入和删除效率低。（如果你从中间插入一个数据，那么这条数据之后的都要往后移，所以相应的效率就比较低）

2 、离散存储：链表（单向，双向，环形）

① 链表：可以不连续，那么链表如何实现存储？

解决了我们数组的插入和删除效率低的问题。

那么对于链表我们如何查询呢？

遍历的时候会增加一个cur变量，开始的时候cur等于我们的头结点。

那么从下图我们可以看出，数据之间通过在上一个存储空间存有指向下一个存储空间的地址的方式。

 3 、链表操作：

  ① 单向链表操作：

查、增、改、删

class Hero(object):
    def __init__(self, no=None, nickname=None, name=None, pNext = None):
        self.no = no
        self.nickname = nickname
        self.name = name
        self.pNext = pNext

#### 添加节点
def addHero(head, pNew):
    cur = head
    # while cur.pNext != None:
    #     cur = cur.pNext
    #
    # cur.pNext = pNew

    while cur.pNext != None:
        if cur.pNext.no > pNew.no:
            break

        cur = cur.pNext

    pNew.pNext = cur.pNext
    cur.pNext = pNew

    
#### 遍历节点
def showHero(head):
    if isEmpty(head):
        return None

    cur = head

    while cur.pNext != None:
        print("英雄的编号是: %s, 外号是：%s, 姓名:%s" % (cur.pNext.no, cur.pNext.nickname, cur.pNext.name))
        cur = cur.pNext
### 判断是否为空
def isEmpty(head):
    if head.pNext != None:
        return False
    return True

## 删除节点
def delHero(head, no):
    cur = head
    while cur.pNext != None:
        if cur.pNext.no == no:
            # 开始删除
            cur.pNext = cur.pNext.pNext
            break
        cur = cur.pNext
    else:
        print('没有找到好汉')

### 链表的长度
def getLength(head):
    length = 0
    cur = head
    while cur.pNext != None:
        cur = cur.pNext
        length = length + 1

    return length

### 更新链表
def updateHero(head, no, name):
    cur = head
    while cur.pNext != None:
        if cur.pNext.no == no:
            cur.pNext.name = name
            break
        cur = cur.pNext
    else:
        print('没有找到好汉')


# 头结点
head = Hero()

## 首节点
h1 = Hero(1, '及时雨', '宋江')
h2 = Hero(2, '玉麒麟', '卢俊义')
h3 = Hero(6, '豹子头', '林冲')
h4 = Hero(4, '入云龙', '公孙胜')
h5 = Hero(5, '行者', '武松')

addHero(head, h1)
addHero(head, h2)
addHero(head, h3)
addHero(head, h4)
addHero(head, h5)

showHero(head)
print(getLength(head))

 ② 双向链表：

表中每个节点有两个指针：一个指向后面节点、一个指向前面节点

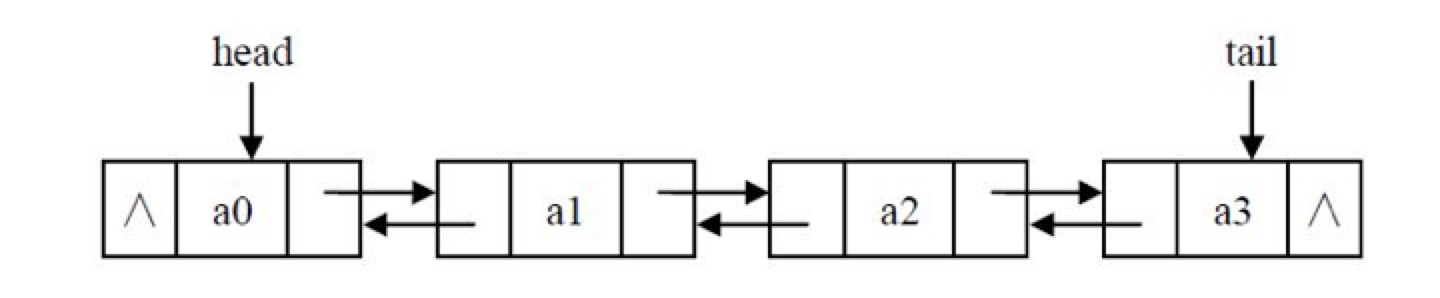
class Node(object):
def __init__(self, data=None):
self.data = data
self.next = None
self.prior = None

插入：

p.next = curNode.next
curNode.next.prior = p
curNode.next = p
p.prior = curNode

删除：

p = curNode.next
curNode.next = p.next
p.next.prior = curNode
del p

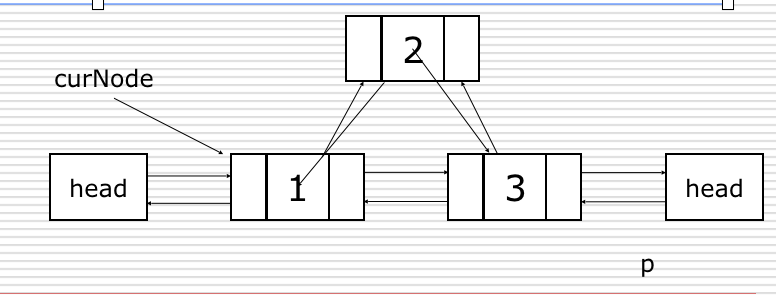
 ③ 环形链表

循环链表是另一种形式的链式存贮结构。它的特点是表中最后一个结点的指针域指向头结点，整个链表形成一个环。

 ④ 约瑟夫问题 

编号为1，2，… n的n个人围坐一圈，约定编号为k（1<=k<=n）的人从1开始报数，数到m 的那个人出列，它的下一位又从1开始报数，数到m的那个人又出列，依次类推，直到所有人出列为止，
由此产生一个出队编号的序列

class Child(object):
    first = None

    def __init__(self, no=None, pNext=None):
        self.no = no
        self.pNext = pNext

    def addChild(self, n):
        cur = None
        for i in range(n):
            child = Child(i + 1)

            if i == 0:
                self.first = child
                child.pNext = self.first
                cur = self.first
            else:
                cur.pNext = child
                child.pNext = self.first
                cur = cur.pNext

    def showChild(self):
        cur = self.first

        while cur.pNext != self.first:
            print("当前孩子的编号是：%s" % cur.no)
            cur = cur.pNext

        print("当前孩子的编号是：%s" % cur.no)

    def countChild(self, m, k):
        tail = self.first

        while tail.pNext != self.first:
            tail = tail.pNext

        #### 当退出循环的时候，tail已经是在first的后面了

        for i in range(k - 1):
            tail = tail.pNext
            self.first = self.first.pNext

        while tail != self.first:
            for i in range(1):
                tail = tail.pNext
                self.first = self.first.pNext

            self.first = self.first.pNext
            tail.pNext = self.first

        print("最终剩下的孩子的编号是: %s" % self.first.no)


c = Child()
c.addChild(1000)
c.showChild()
c.countChild(3, 2)