1. 介绍
1.1. 论文提出的背景
虽然在一般情况下,我们不会去区分训练和部署使用的模型,但是训练和部署之间存在着一定的不一致性:
- 在训练过程中,我们需要使用复杂的模型,大量的计算资源,以便从非常大、高度冗余的数据集中提取出信息。在实验中,效果最好的模型往往规模很大,甚至由多个模型集成得到。而大模型不方便部署到服务中去,常见的瓶颈如下:
- 推断速度慢
- 对部署资源要求高(内存,显存等)
- 在部署时,我们对延迟以及计算资源都有着严格的限制。
因此,模型压缩(在保证性能的前提下减少模型的参数量)成为了一个重要的问题。而”模型蒸馏“属于模型压缩的一种方法。
插句题外话,我们可以从模型参数量和训练数据量之间的相对关系来理解underfitting和overfitting。AI领域的从业者可能对此已经习以为常,但是为了力求让小白也能读懂本文,还是引用我同事的解释(我印象很深)形象地说明一下:
模型就像一个容器,训练数据中蕴含的知识就像是要装进容器里的水。当数据知识量(水量)超过模型所能建模的范围时(容器的容积),加再多的数据也不能提升效果(水再多也装不进容器),因为模型的表达空间有限(容器容积有限),就会造成underfitting;而当模型的参数量大于已有知识所需要的表达空间时(容积大于水量,水装不满容器),就会造成overfitting,即模型的variance会增大(想象一下摇晃半满的容器,里面水的形状是不稳定的)。
1.2. “思想歧路”
上面容器和水的比喻非常经典和贴切,但是会引起一个误解: 人们在直觉上会觉得,要保留相近的知识量,必须保留相近规模的模型。也就是说,一个模型的参数量基本决定了其所能捕获到的数据内蕴含的“知识”的量。
这样的想法是基本正确的,但是需要注意的是:
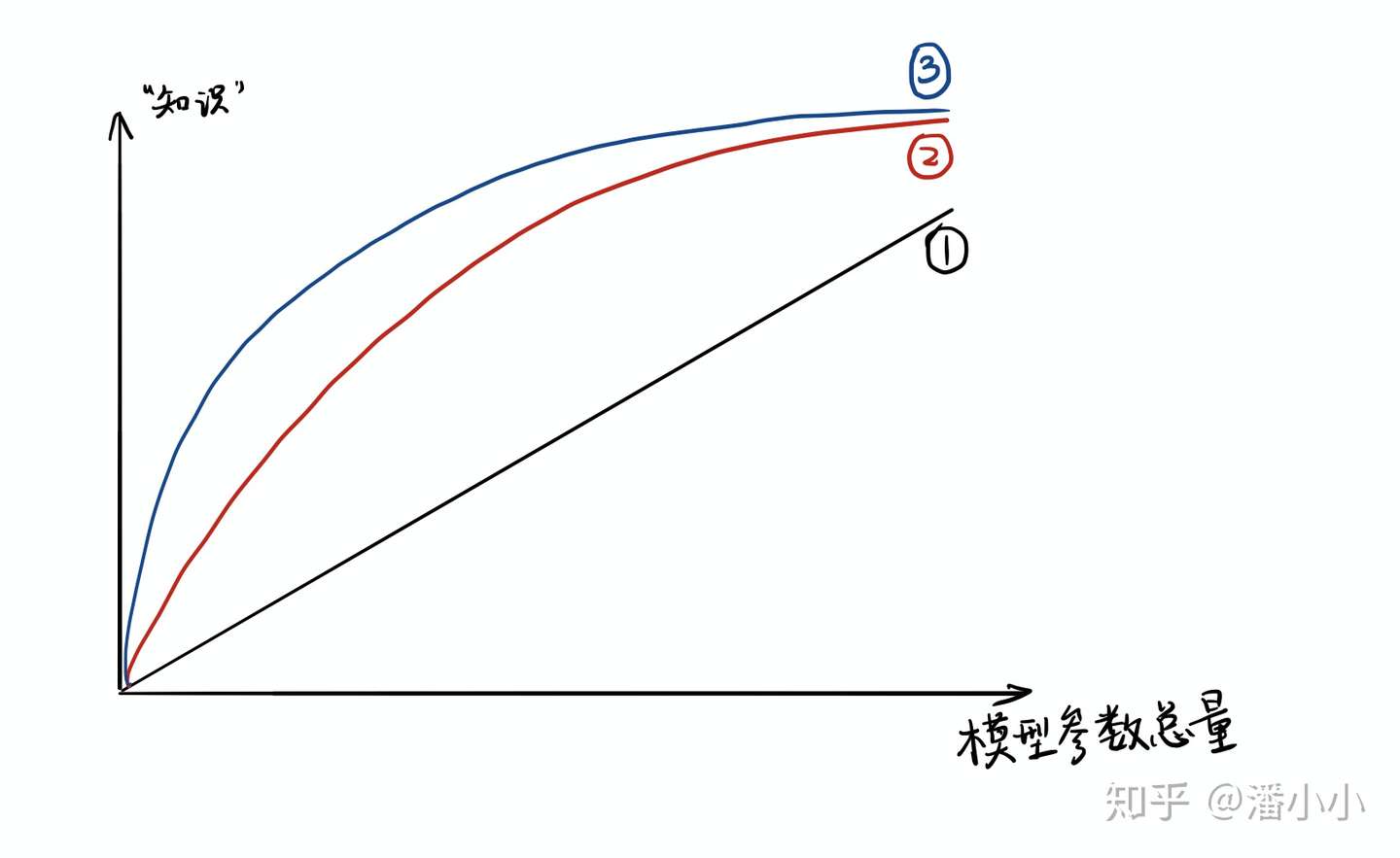
- 模型的参数量和其所能捕获的“知识“量之间并非稳定的线性关系(下图中的1),而是接近边际收益逐渐减少的一种增长曲线(下图中的2和3)
- 完全相同的模型架构和模型参数量,使用完全相同的训练数据,能捕获的“知识”量并不一定完全相同,另一个关键因素是训练的方法。合适的训练方法可以使得在模型参数总量比较小时,尽可能地获取到更多的“知识”(下图中的3与2曲线的对比).
2. 知识蒸馏的理论依据
2.1. Teacher Model和Student Model
知识蒸馏使用的是Teacher—Student模型,其中teacher是“知识”的输出者,student是“知识”的接受者。知识蒸馏的过程分为2个阶段:
- 原始模型训练: 训练"Teacher模型", 简称为Net-T,它的特点是模型相对复杂,也可以由多个分别训练的模型集成而成。我们对"Teacher模型"不作任何关于模型架构、参数量、是否集成方面的限制,唯一的要求就是,对于输入X, 其都能输出Y,其中Y经过softmax的映射,输出值对应相应类别的概率值。
- 精简模型训练: 训练"Student模型", 简称为Net-S,它是参数量较小、模型结构相对简单的单模型。同样的,对于输入X,其都能输出Y,Y经过softmax映射后同样能输出对应相应类别的概率值。
在本论文中,作者将问题限定在分类问题下,或者其他本质上属于分类问题的问题,该类问题的共同点是模型最后会有一个softmax层,其输出值对应了相应类别的概率值。
2.2. 知识蒸馏的关键点
如果回归机器学习最最基础的理论,我们可以很清楚地意识到一点(而这一点往往在我们深入研究机器学习之后被忽略): 机器学习最根本的目的在于训练出在某个问题上泛化能力强的模型。
- 泛化能力强: 在某问题的所有数据上都能很好地反应输入和输出之间的关系,无论是训练数据,还是测试数据,还是任何属于该问题的未知数据。
而现实中,由于我们不可能收集到某问题的所有数据来作为训练数据,并且新数据总是在源源不断的产生,因此我们只能退而求其次,训练目标变成在已有的训练数据集上建模输入和输出之间的关系。由于训练数据集是对真实数据分布情况的采样,训练数据集上的最优解往往会多少偏离真正的最优解(这里的讨论不考虑模型容量)。
而在知识蒸馏时,由于我们已经有了一个泛化能力较强的Net-T,我们在利用Net-T来蒸馏训练Net-S时,可以直接让Net-S去学习Net-T的泛化能力。
一个很直白且高效的迁移泛化能力的方法就是:使用softmax层输出的类别的概率来作为“soft target”。
【KD的训练过程和传统的训练过程的对比】
- 传统training过程(hard targets): 对ground truth求极大似然
- KD的training过程(soft targets): 用large model的class probabilities作为soft targets
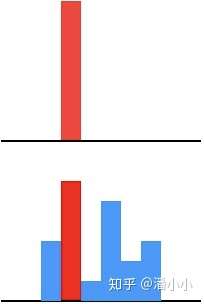 上图: Hard Target 下图: Soft Target
上图: Hard Target 下图: Soft Target
KD的训练过程为什么更有效?
softmax层的输出,除了正例之外,负标签也带有大量的信息,比如某些负标签对应的概率远远大于其他负标签。而在传统的训练过程(hard target)中,所有负标签都被统一对待。也就是说,KD的训练方式使得每个样本给Net-S带来的信息量大于传统的训练方式。
【举个例子】
在手写体数字识别任务MNIST中,输出类别有10个。
 MNIST任务
MNIST任务
假设某个输入的“2”更加形似"3",softmax的输出值中"3"对应的概率为0.1,而其他负标签对应的值都很小,而另一个"2"更加形似"7","7"对应的概率为0.1。这两个"2"对应的hard target的值是相同的,但是它们的soft target却是不同的,由此我们可见soft target蕴含着比hard target多的信息。并且soft target分布的熵相对高时,其soft target蕴含的知识就更丰富。
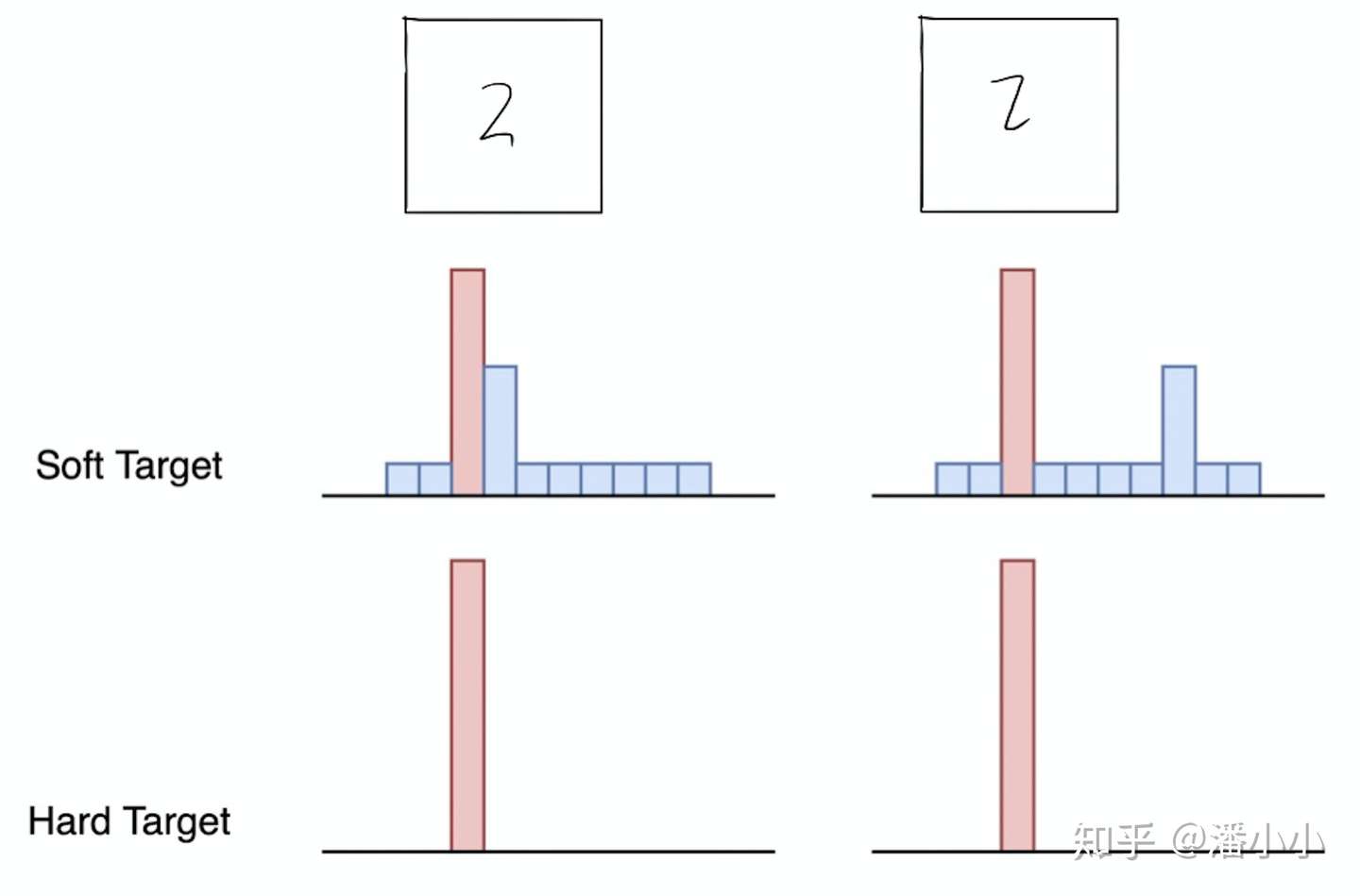 两个”2“的hard target相同而soft target不同
两个”2“的hard target相同而soft target不同
这就解释了为什么通过蒸馏的方法训练出的Net-S相比使用完全相同的模型结构和训练数据只使用hard target的训练方法得到的模型,拥有更好的泛化能力。
2.3. softmax函数
先回顾一下原始的softmax函数:
但要是直接使用softmax层的输出值作为soft target, 这又会带来一个问题: 当softmax输出的概率分布熵相对较小时,负标签的值都很接近0,对损失函数的贡献非常小,小到可以忽略不计。因此"温度"这个变量就派上了用场。
下面的公式时加了温度这个变量之后的softmax函数:
- 这里的T就是温度。
- 原来的softmax函数是T = 1的特例。 T越高,softmax的output probability distribution越趋于平滑,其分布的熵越大,负标签携带的信息会被相对地放大,模型训练将更加关注负标签。
3. 知识蒸馏的具体方法
3.1. 通用的知识蒸馏方法
- 第一步是训练Net-T;第二步是在高温T下,蒸馏Net-T的知识到Net-S
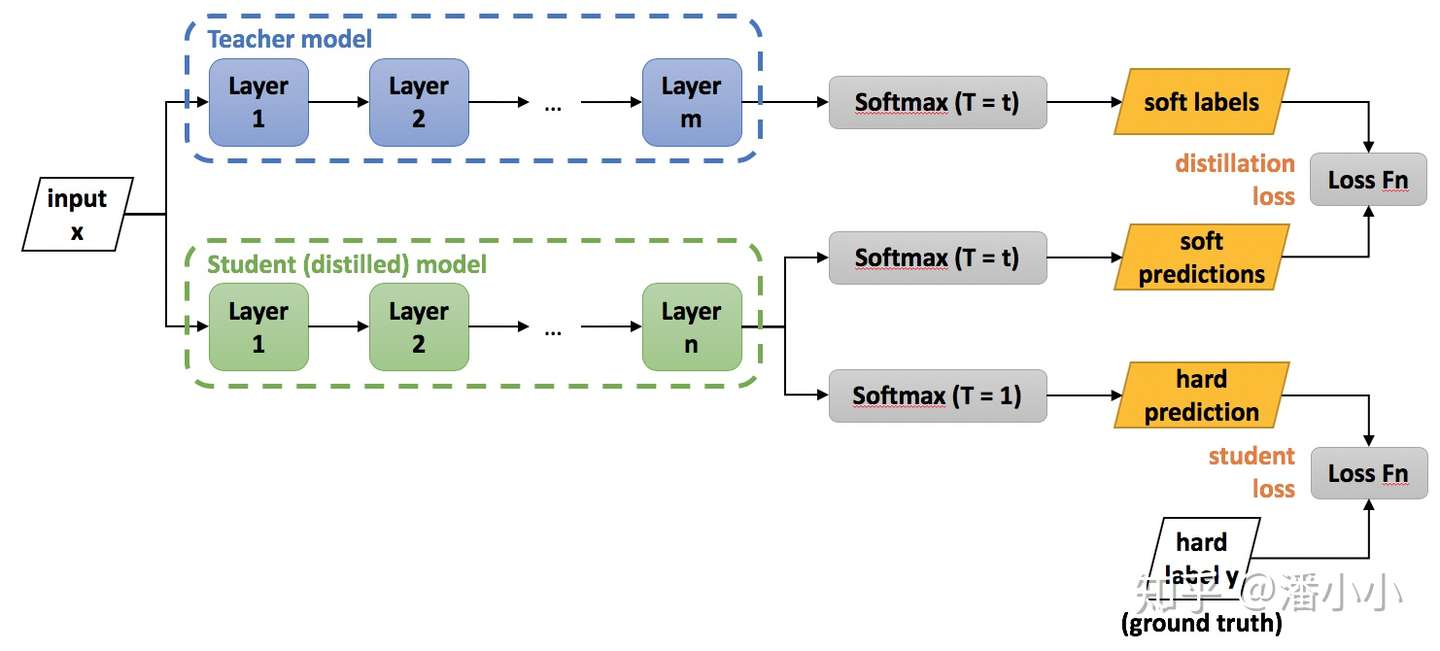 知识蒸馏示意图(来自https://nervanasystems.github.io/distiller/knowledge_distillation.html)
知识蒸馏示意图(来自https://nervanasystems.github.io/distiller/knowledge_distillation.html)
训练Net-T的过程很简单,下面详细讲讲第二步:高温蒸馏的过程。高温蒸馏过程的目标函数由distill loss(对应soft target)和student loss(对应hard target)加权得到。示意图如上。
: Net-T的logits
: Net-S的logits
: Net-T的在温度=T下的softmax输出在第i类上的值
: Net-S的在温度=T下的softmax输出在第i类上的值
: 在第i类上的ground truth值,
, 正标签取1,负标签取0.
: 总标签数量
- Net-T 和 Net-S同时输入 transfer set (这里可以直接复用训练Net-T用到的training set), 用Net-T产生的softmax distribution (with high temperature) 来作为soft target,Net-S在相同温度T条件下的softmax输出和soft target的cross entropy就是Loss函数的第一部分
,其中
,
- Net-S在T=1的条件下的softmax输出和ground truth的cross entropy就是Loss函数的第二部分
。
,其中
- 第二部分Loss
的必要性其实很好理解: Net-T也有一定的错误率,使用ground truth可以有效降低错误被传播给Net-S的可能。打个比方,老师虽然学识远远超过学生,但是他仍然有出错的可能,而这时候如果学生在老师的教授之外,可以同时参考到标准答案,就可以有效地降低被老师偶尔的错误“带偏”的可能性。
【讨论】
- 实验发现第二部分所占比重比较小的时候,能产生最好的结果,这是一个经验的结论。一个可能的原因是,由于soft target产生的gradient与hard target产生的gradient之间有与
相关的比值。原论文中只是一笔带过,我在下面补充了一些简单的推导。
- Soft Target:
- Hard Target:
- 由于
的magnitude大约是
的
,因此在同时使用soft target和hard target的时候,需要在soft target之前乘上
的系数,这样才能保证soft target和hard target贡献的梯度量基本一致。
【注意】 在Net-S训练完毕后,做inference时其softmax的温度T要恢复到1.
3.2. 一种特殊情形: 直接match logits(不经过softmax)
直接match logits指的是,直接使用softmax层的输入logits(而不是输出)作为soft targets,需要最小化的目标函数是Net-T和Net-S的logits之间的平方差。
直接上结论: 直接match logits的做法是 的情况下的特殊情形。
由单个case贡献的loss,推算出对应在Net-S每个logit 上的gradient:
当 时,我们使用
来近似
,于是得到
如果再加上logits是零均值的假设
那么上面的公式可以简化成
也就是等价于minimise下面的损失函数
4. 关于"温度"的讨论
【问题】 我们都知道“蒸馏”需要在高温下进行,那么这个“蒸馏”的温度代表了什么,又是如何选取合适的温度?
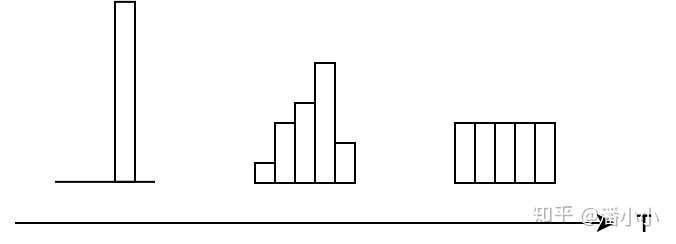 随着温度T的增大,概率分布的熵逐渐增大
随着温度T的增大,概率分布的熵逐渐增大
4.1. 温度的特点
在回答这个问题之前,先讨论一下温度T的特点
- 原始的softmax函数是
时的特例,
时,概率分布比原始更“陡峭”,
时,概率分布比原始更“平缓”。
- 温度越高,softmax上各个值的分布就越平均(思考极端情况: (i)
, 此时softmax的值是平均分布的;(ii)
,此时softmax的值就相当于
, 即最大的概率处的值趋近于1,而其他值趋近于0)
- 不管温度T怎么取值,Soft target都有忽略相对较小的
携带的信息的倾向
4.2. 温度代表了什么,如何选取合适的温度?
温度的高低改变的是Net-S训练过程中对负标签的关注程度: 温度较低时,对负标签的关注,尤其是那些显著低于平均值的负标签的关注较少;而温度较高时,负标签相关的值会相对增大,Net-S会相对多地关注到负标签。
实际上,负标签中包含一定的信息,尤其是那些值显著高于平均值的负标签。但由于Net-T的训练过程决定了负标签部分比较noisy,并且负标签的值越低,其信息就越不可靠。因此温度的选取比较empirical,本质上就是在下面两件事之中取舍:
- 从有部分信息量的负标签中学习 --> 温度要高一些
- 防止受负标签中噪声的影响 -->温度要低一些
总的来说,T的选择和Net-S的大小有关,Net-S参数量比较小的时候,相对比较低的温度就可以了(因为参数量小的模型不能capture all knowledge,所以可以适当忽略掉一些负标签的信息)
5. 参考
- 深度压缩之蒸馏模型 - 风雨兼程的文章 - 知乎 https://zhuanlan.zhihu.com/p/24337627
- 知识蒸馏Knowledge Distillation - 船长的文章 - 知乎 https://zhuanlan.zhihu.com/p/83456418
- https://towardsdatascience.com/knowledge-distillation-simplified-dd4973dbc764
- https://zhuanlan.zhihu.com/p/102038521