一、P vs. NP
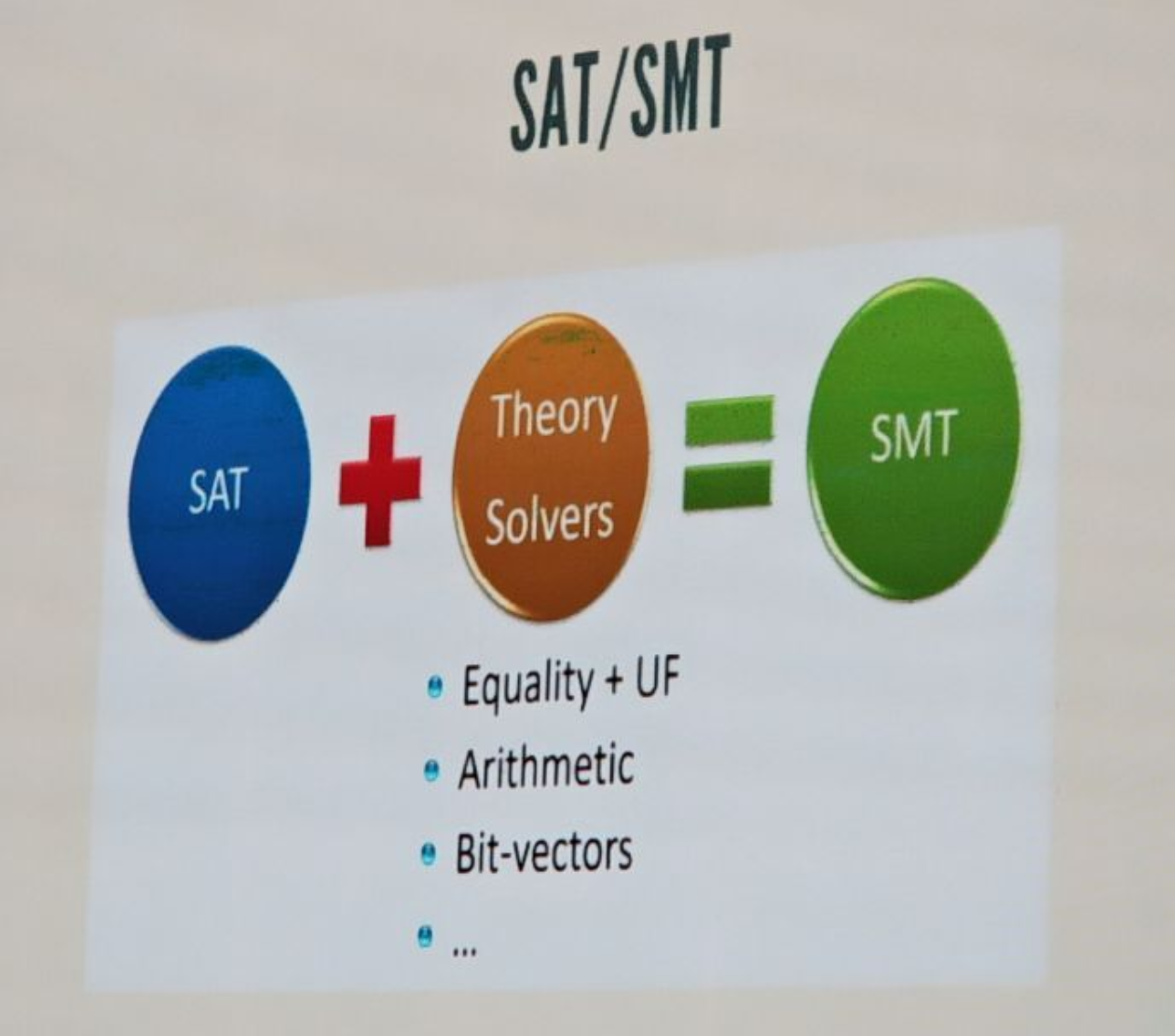
- P: 能在多项式时间内解决的问题。
- NP: 不能在多项式时间内解决或不确定能不能在多项式时间内解决,但能在多项式时间验证的问题。
- NPC: NP完全问题,所有NP问题在多项式时间内都能约化(Reducibility)到它的NP问题,即解决了此NPC问题,所有NP问题也都得到解决。
- NP hard:NP难问题,所有NP问题在多项式时间内都能约化(Reducibility)到它的问题(不一定是NP问题)。
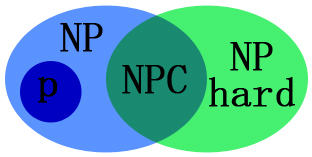
二、SAT问题
- 应用:
Hardware Model Checking(All major hardware companies (Intel, ...) use SAT sovler to verify their chip desgins)
Software Verification
1.SAT solver based SMT solvers are used to verify Microsoft software products
2.Embedded software in Cars, Aiplanes, Refrigerators, ...
3.Unix utilities
Automated Planning and Scheduling(Still one of the best approaches for optimal planning)
Number Theoretic Problems (Pythagorean Triples)
**Solving other NP-hard problems **(coloring, clique, ...)
- Who is Lying
Questions:
A: B is lying.
B: C is lying.
C: A and B is lying.
so, who is not lying?
Encoding:
3 variables: a, b, c present A, B, C speak truth, while ¬a, ¬b, ¬c present lying.
**clauses: **
a V b V c ; %at least one speak truth.
¬ a V ¬ b; a V b; %a-> ¬b, ¬a -> b
¬ b V ¬ c; b V c; %b-> ¬c, ¬b -> c
¬ c V ¬ a; ¬c V ¬b; c V a V b %c->(¬aꓥ ¬b), ¬c->¬ (¬aꓥ ¬b)
result: ¬a, b, ¬c
b speaks truth, a, c are lying
- MaxSAT问题
对于某些问题,是不可满足的。那么需要关注如何尽可能地满足,即 MaxSAT。
- Partial MaxSAT
满足所有的硬子句(hard clauses),尽可能地满足软子句(soft clauses)。
- Weighted Partial MaxSAT
满足所有的硬子句(hard clauses)和最大权重的软子句(soft clauses)
- Satisfiability Modulo Theories (SMT)
参考