机器学习之SVM（支持向量机）

支持向量机（SVM）是当前非常流行的监督学习方法，其核心主要有两个：

1. 构造一个极大边距分离器——与样例点具有最大可能距离的决策边界；
2. 将在原输入空间中线性不可分的样例映射到高维空间中，从而进行线性分离。并且使用核技巧来避免高维度空间的运算所带来的巨大时间复杂度。

极大边距分离器

假设我们想构造一个线性分类器，如下图所示：

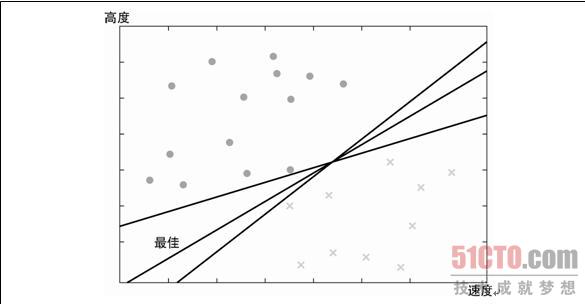
我们有无数的选择，那么哪个选择才是最优的呢？直观上观察，我们希望选择距离样例最远的分类器，因为分类器距离样例越近，那么当与该样例相近的真实样例很有可能就落在了直线的另一边，从而被错误分类。SVM把这样一个分类器叫做极大边距分离器：

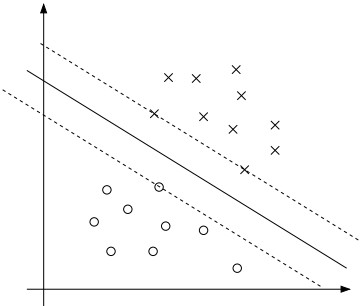
如上图中的中间的那条实线就是我们想要找的极大边距分离器。

极大边距分离器的发现

分离器定义为点的集合{x:w•x + b = 0},我们的任务就是找到w。这样当新样例x来的时候，我们带入y = w • x + b中，如果y >= 1则为正类；y <= -1则为负类；如果在(-1,1)之间则拒绝分类。
为了找到w，我们需要求解最大化下列公式的α：

并满足约束:

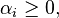 和

求得α后，通过下列公式可以求得w：

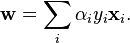
核技巧

当样例在原输入空间线性不可分的时候，我们发现将样例映射到高维空间中就可以轻易将样例分离开来：

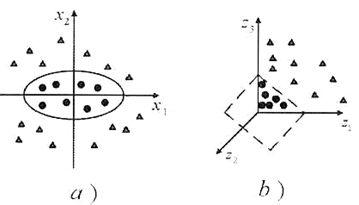
例如上图，我们把a）中的样例(x₁, x₂)映射成向量F（x） = (z₁, z₂, z₃), 其中：

z₁ = x₁²
z₂ = x₂²
z₃ = 2 x₁x₂

于是我们将F（x_i) • F（x_j) 取代下列公式中的x_i • x_j：

从而求得在高维空间中的线性分离器。
但是我们可以发现：
   F（x_i) • F（x_j) = (x_i • x_j)²
因此我们可以先求x_j • x_j，再平方求得F（x_i) • F（x_j)。我们称：
   K（x_i，x_j) = (x_i • x_j)²
为核函数。
因为在一些情况中x_i和 x_j的维度可能会远远小于F（x_i)和F（x_j)，因此使用核函数进行求解可以避免在高维度空间进行计算，从而大大减小时间复杂度。

总结

最后总结下SVM学习算法的基本步骤：

1. 求解下列最优化问题：
   
   并满足约束:
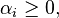     和
    
2. 计算最优权值w:
   
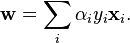
3. 将真实样例x代入下列公式中对其进行分类。
   y = w • x + b