时间序列分析又叫时间数列分析。时间序列又称动态数列或时间数列。时间序列是指将某种现象某一个统计指标在不同时间上的各个数值,按时间先后顺序排列而形成的序列。时间序列法是一种定量预测方法,亦称简单外延方法,在统计学中作为一种常用的预测手段被广泛应用。时间序列分析在第二次世界大战前应用于经济预测。二次大战中和战后,在军事科学、空间科学、气象预报和工业自动化等部门的应用更加广泛。时间序列分析(Time series analysis)是一种动态数据处理的统计方法。该方法基于随机过程理论和数理统计学方法,研究随机数据序列所遵从的统计规律,以用于解决实际问题。时间序列构成要素是:现象所属的时间,反映现象发展水平的指标数值。
时间序列的作用
- 深入揭示现象变化的数值特征
- 反映现象发展变化的趋势和规律
- 揭示现象变化的内在原因,为预测和决策提供可靠的数量信息
- 描述社会经济现象发展过程与结果
- 用于计算水平分析指标和速度分析指标,研究现象的发展速度和趋势
- 通过建立数学模型,揭示现象的发展变化规律性,并预测发展趋势
- 揭示现象之间的相互联系程度及其动态演变关系
时间序列的分类
平稳序列(stationary series)
- 基本上不存在趋势的序列,各观察值基本上在某个固定的水平上波动
- 或虽有波动,但并不存在某种规律,而其波动可以看成是随机的
非平稳序列(non-stationary series)
- 有趋势的序列
线性的,非线性的
- 有趋势、季节性和周期性的复合型序列
时间序列的种类

绝对数时间序列
- 一系列绝对数按时间顺序排列而成
- 时间序列中最基本的表现形式
- 反映现象在不同时间上所达到的绝对水平
- 分为时期序列(时期数列)和时点序列(时点数列)
时期序列:现象在一段时期内总量的排序
时点序列:现象在某一瞬间时点上总量的排序
相对数时间序列
一系列相对数按时间顺序排列而成
平均数时间序列
一系列平均数按时间顺序排列而成
按研究对象的数量分类
- 一元时间序列
- 多元时间序列
按时间的连续性分类
- 离散型时间序列
- 连续型时间序列
按变量值的表现形式
- 绝对数时间序列
- 相对数时间序列
- 平均数时间序列
时间序列的成分
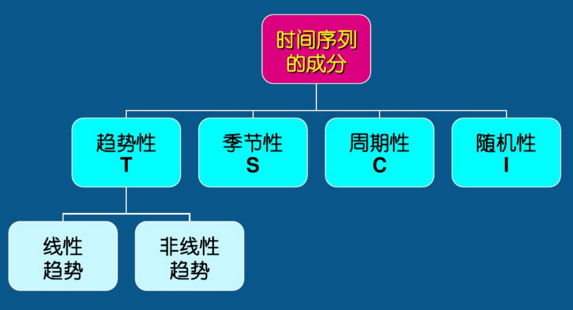
趋势性(trend)
持续向上或持续下降的状态或规律
季节性(seasonality)
- 也称季节变动(Seasonal fluctuation)
- 时间序列在一年内重复出现的周期性波动
周期性(cyclity)
- 也称循环波动(cyclical fluctuation)
- 围绕长期趋势的一种波浪形或振荡式变动
随机性(random)
- 也称不规则波动(irregular variations)
- 除去趋势、周期性和季节性之后的偶然性波动
构成时间序列的因素
构成要素:两部分组成
- 现象所属的时间t(年份、季度、月份或其他任何时间形式)
- 现象在不同时间上的观察值Y
时间序列的构成,是因为现象的发展变化时多种因素影响的综合结果,由于各种因素的作用方向和影响程度不同,使具体的时间序列呈现出不同的变动形态
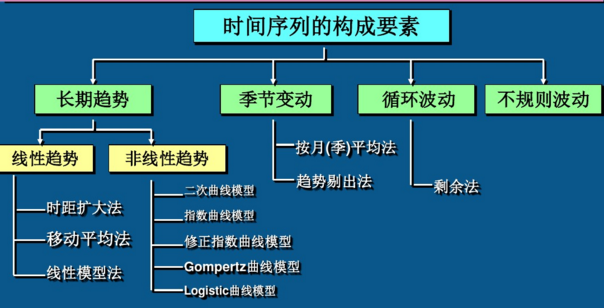
时间序列分析的任务就是要正确地确定时间序列的性质,对影响时间序列的各种因素加以分解和测定,以便对未来的状况作出判断和预测。这些因素按照性质可以划分为:长期趋势、季节变动、循环变动、不规则变动
长期趋势
由于某种根本原因的影响,客观现象在一个相当长的时间内所呈现出来的持续增加或持续减少的一种趋势和状态
季节变动
由于季节的转变而使时间序列发生周期性变化。这种周期性变化时以年为周期的可以预见的变化,因而反映季节变化的时间序列的数值资料所属的时间一般以月、季、周等为单位,而不以年为单位。引起季节变化的因素有自然因素,也有人为因素
循环变动
循环变动是指时间序列以若干年为周期的波浪式变动。这种变动的特征:现象的增加或减少交替出现,但持续的周期不因它的波动按任何既定的趋势变化,而是按照某种不可预测方式进行涨落起伏 波动,最典型的周期波动是商业周期
不规则变动
由于一些随机因素的影响,而是时间序列产生的不可预测的不规则变动
以上四种影响因素有时可能同时出现,共同影响某一现象的变化,有时也可能只有几种因素起作用。一般情况下,长期趋势是影响时间序列变动的基本因素。上述四种因素和现象总量之间的关系可以是:
加法模型:现象总量=长期趋势+季节变动+循环变动+不规则变动(适用于四种因素相互独立的情况)
乘法模型:现象总量=长期趋势*季节变动*循环变动*不规则变动
时间序列的编制原理
时间长短(或间隔)一致
- 时间序列,各指标值所属时间长短应一致
- 时点序列,各指标的时间点间隔应一致
口径一致
- 总体范围一致
- 计量单位一致
- 经济内容一致
- 计算价格一致
计算方法一致
时间序列的水平分析
发展水平与平均发展水平
1.发展水平
- 现象在不同的时间上的观察值
- 说明现象在某一时间上所达到的水平
- 表示为Y1,Y2,...,Yn或Y0,Y1,Y2,...,Yn
2.平均发展水平
- 现象在不同时间上取值的平均数,又称序时平均数
- 说明现象在一段时期内所达到的一般水平
- 不同类型的时间序列有不同的计算方法
时间序列
1.绝对数时间序列的序时平均数(计算方法)
时期序列
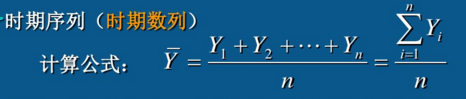
对于连续时点序列(时点数列)计算序时平均数也可使用以上公式
时点序列
间隔时点序列——间隔不相等
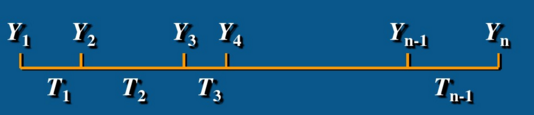

间断时间序列——间隔相等

2.相对数或平均数时间序列的序时平均数

增长量与平均增长量
1.增长量(又称为增减量)(概念、种类、计算方法)

2.平均增长量(概念及计算方法)

时间序列的速度分析
发展速度与增长速度(增长率)
1.发展速度的概念、种类、计算方法



2.增长速度(增长率)的概念、种类、计算方法


平均发展速度与平均增长速度(平均增长率)





时间序列分解分析
时间序列的构成要素与模型
如果时间序列存在某种规律性的变动,通常称为非平稳序列(可能包含趋势性、季节性或周期性的序列)

长期趋势分析
1.概念要点
- 现象在较长时期内持续发展变化的一种趋向或状态
- 由影响时间序列的基本因素作用形成
- 时间序列的主要构成要素
- 有线性趋势和非线性趋势
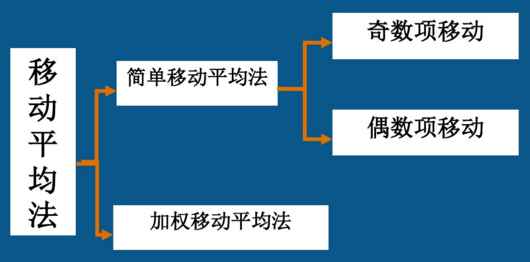
2.长期趋势测定的主要方法
- 时距扩大法
- 移动平均法
- 数学模型法
3.线性趋势分析

移动平均法

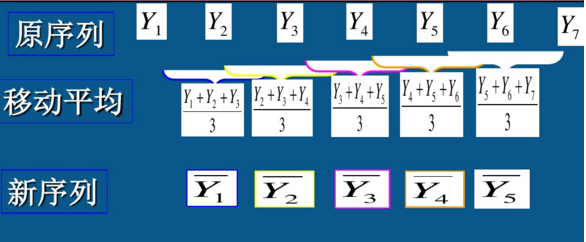
简单移动平均(奇数项移动平均法)
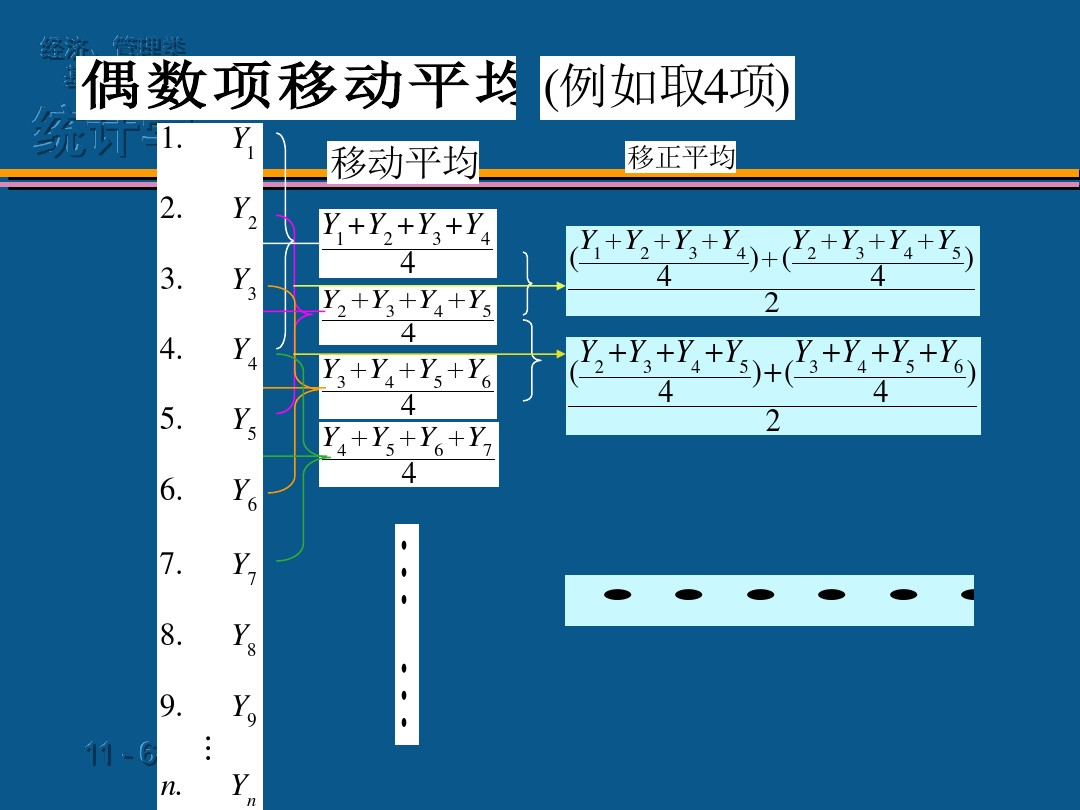
简单移动平均(偶数项移动平均法)

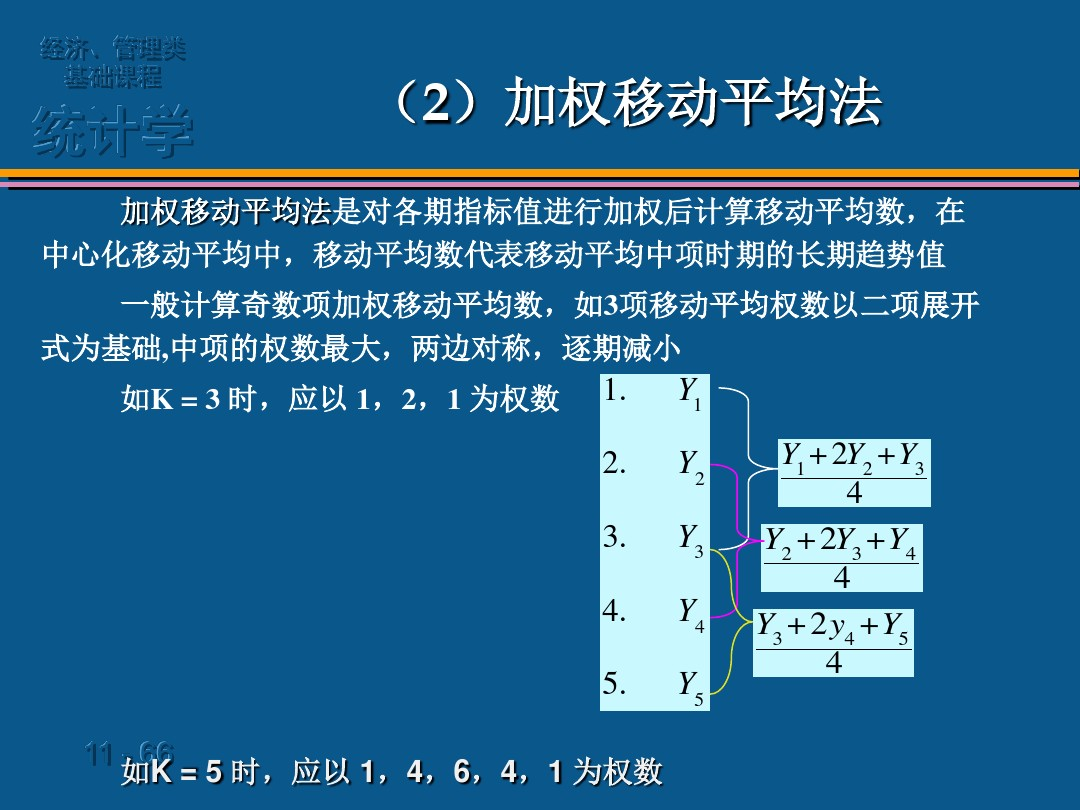
线性模型法



季节变动分析
1.季节变动及其测定目的

2.季节变动的分析方法与原理


3.季节变动的测定
按月(或季)平均法
趋势剔除法

分离季节变动的影响

循环波动分析
1.循环波动概念及其测定目的

2.循环波动的分析方法

