采用移动平均值法进行数字滤波
移动平均值法进行数字滤波,其滤波思想大概是这样。有一个需要进行滤波的数据数组data[n],我们采用移动p点取平均值,
data[0] = (data[0] + data[1] + … + data[0+p])/p
data[1] = (data[1] + data[2] + … + data[1+p])/p
data[2] = (data[2] + data[3] + … + data[2+p])/p
…
data[m] = (data[m] + data[m+1] + … + data[m+p])/p (条件:m+p=n-1)
这样,我们就得到了data[n-p]点前的n-p个点的移动平均值。
而对于data[n-p]点后面的p个点的值,在这里我是这样处理的,取后面剩余的p个点的平均值,然后对这p个点分别赋值。
下面是C#的源代码实现,一共提供了两个函数,主要是为了方便调用,一个是针对一维数组,另一个则是针对二维数组:
/// <summary>
/// 一维数组的移动平均值法数字滤波。
/// </summary>
/// <param name="ps">滤波数据</param>
/// <param name="dLen">数据的长度</param>
/// <param name="p">移动的点数</param>
public void MovePoint(short[] ps, int dLen, int p)
{
int i, j;
int sum = 0;
for (i = 0; i < dLen - p; i++)
{
for (j = 0; j < p; j++)
{
sum += ps[i + j];
}
ps[i] = (short)(sum / p);
sum = 0;
}
for (j = 0; j < p; j++)
{
sum += ps[dLen - p + j];
}
short sum2 = (short)(sum / p);
for (i = dLen - p; i < dLen; i++)
{
ps[i] = sum2;
}
}
/// <summary>
/// 二维数组的移动平均值法数字滤波。
/// </summary>
/// <param name="ps">滤波数据</param>
/// <param name="psary1">二维数组的第一维的下标值</param>
/// <param name="dLen">数据的长度</param>
/// <param name="p">移动的点数</param>
public void MovePoint(short[,] ps, int psary1, int dLen, int p)
{
int i, j;
int sum = 0;
for (i = 0; i < dLen - p; i++)
{
for (j = 0; j < p; j++)
{
sum += ps[psary1, i + j];
}
ps[psary1, i] = (short)(sum / p);
sum = 0;
}
for (j = 0; j < p; j++)
{
sum += ps[psary1, dLen - p + j];
}
short sum2 = (short)(sum / p);
for (i = dLen - p; i < dLen; i++)
{
ps[psary1, i] = sum2;
}
}
下面是滤波效果图:
滤波前:
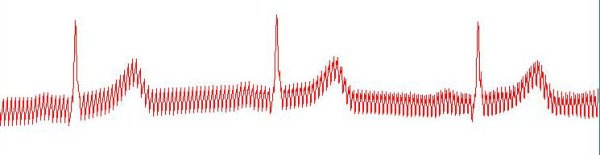
滤波后:

滤波前:
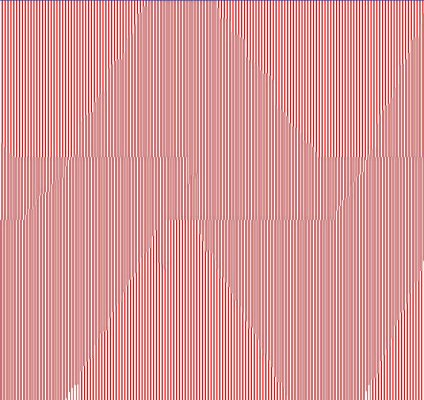
滤波后:
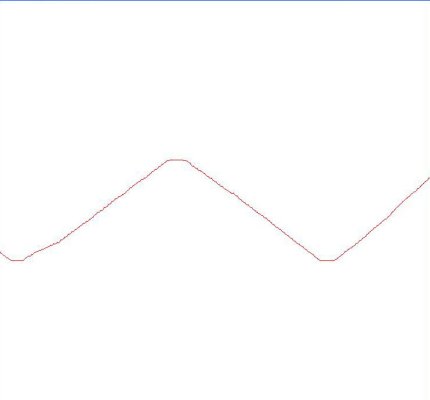
对于移动的p点值是什么确定的呢?我也没有好的办法或根据,只是多试几个值,放5不行,我就放10,10不行就放100,总能找到比较合适的值。当然,p值越大,得到的滤波效果越光滑,但对原来的数据信息的原貌改变得也越大。因此,p最好尽量保持较小的值,这样在得到较好的滤波效果的同时,以更好保持信息原貌。
滤波前:

滤波后:
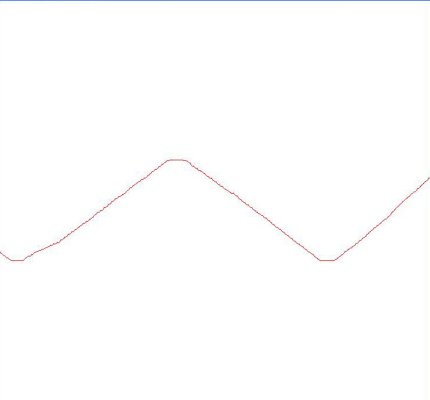
滤波前:
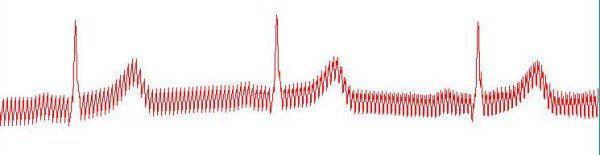
滤波后:
