第二章:词法分析1
2.1 词法分析的任务
编译器的阶段
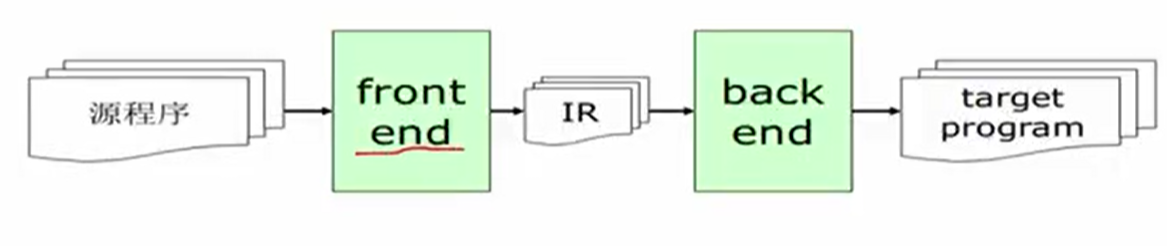
前端处理的是和源语言相关,后端处理的是和体系结构和目标机相关的程序。
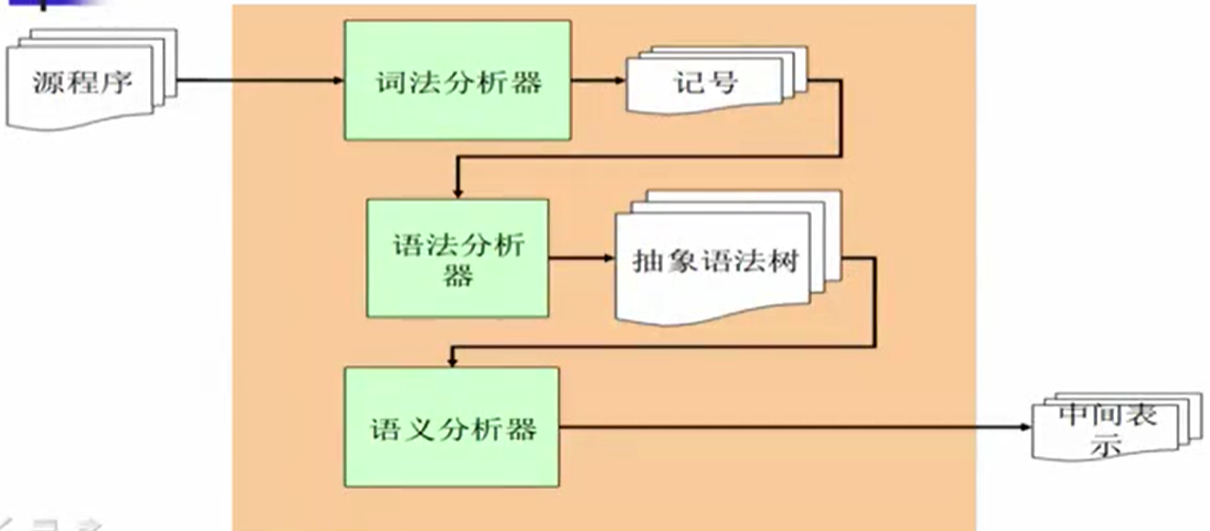
词法分析器的任务

读入字符流后,词法分析器对整个字符流进行切分,按照它们是关键字、标识符、标点符号、字符串、整型数做一个明确的划分。
例子
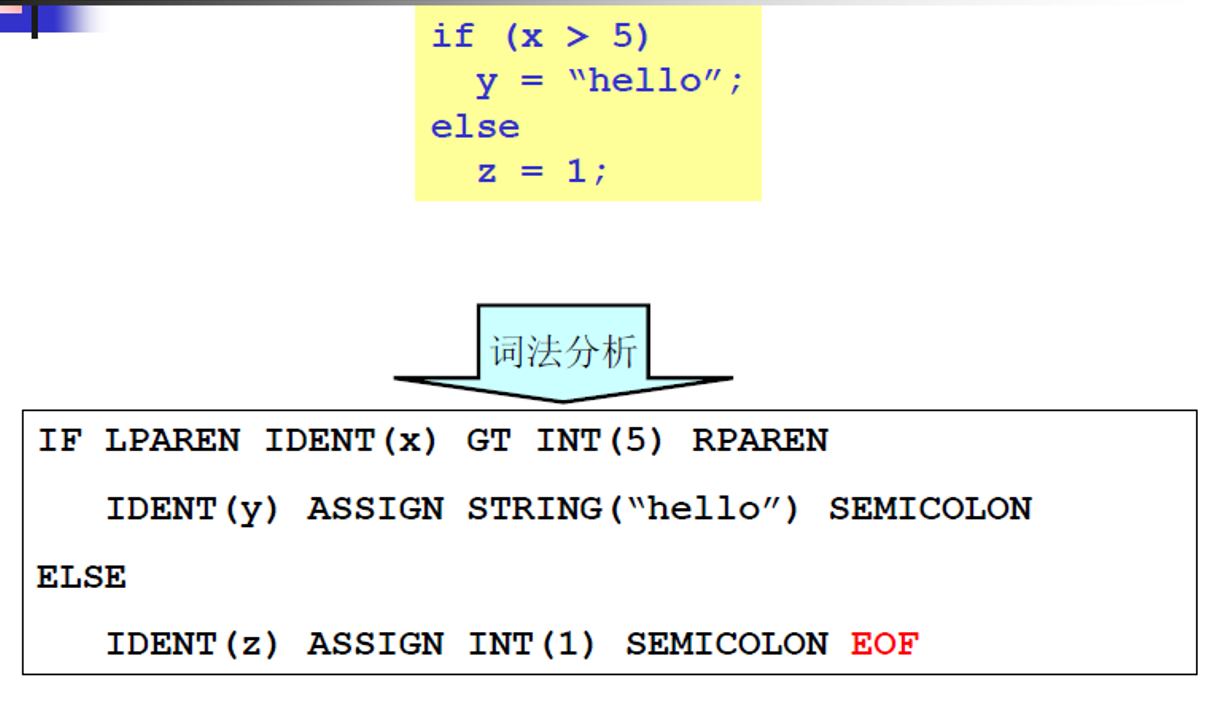
每一个IF、LPAREN等都是记号(单词),结束会有一个EOF。
记号的数据结构

不同的语言,枚举类型是有限的但不一定相同。
lexeme是所识别的单词的具体的值。
if(x>5)
token{ k = IF, lexeme = 0};
token{ k = LPAREN, lexeme = 0};
token{ k = ID, lexeme = 'x'};
小结
- 词法分析器的任务:字符流到记号流
- 字符流:
- 和被编译的语言密切相关(ASCII,Unicode,...)
- 记号流:
- 编译器内部定义的数据结构,编码所识别出的词法单元(记号)
- 字符流:
2.2 词法分析器的手工构造
描述任何一个软件系统最重要的可能都是输入输出接口。
词法分析器的实现方法
- 手工编码实现法
- 相对复杂、且容易出错
- 但是目前流行
- GCC、LLVM、...
- 对程序的各个部分都会有精确的控制,算法和数据结构都是由程序员控制的。
- 效率高
- 词法分析器的生成器
- 快速原型、代码量少
- 较难控制细节
转移图
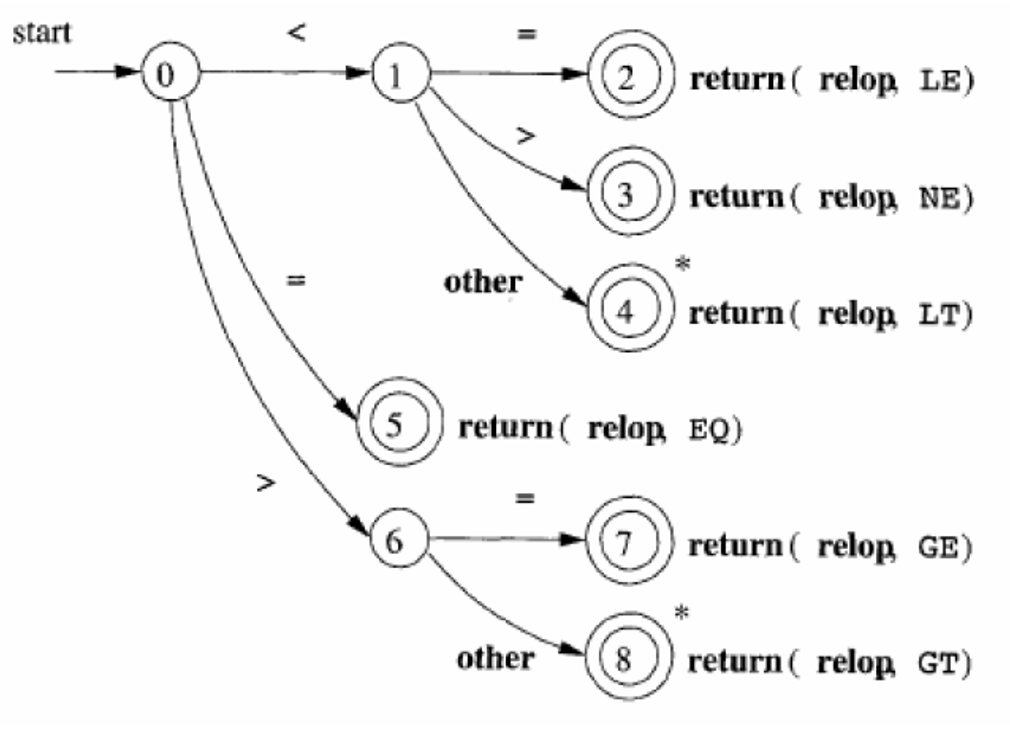
如何分析符号
<= LE
<> NE
< LT
= EQ
>= GE
> GT
*代表一次回退
转移图算法

标识符的转移图
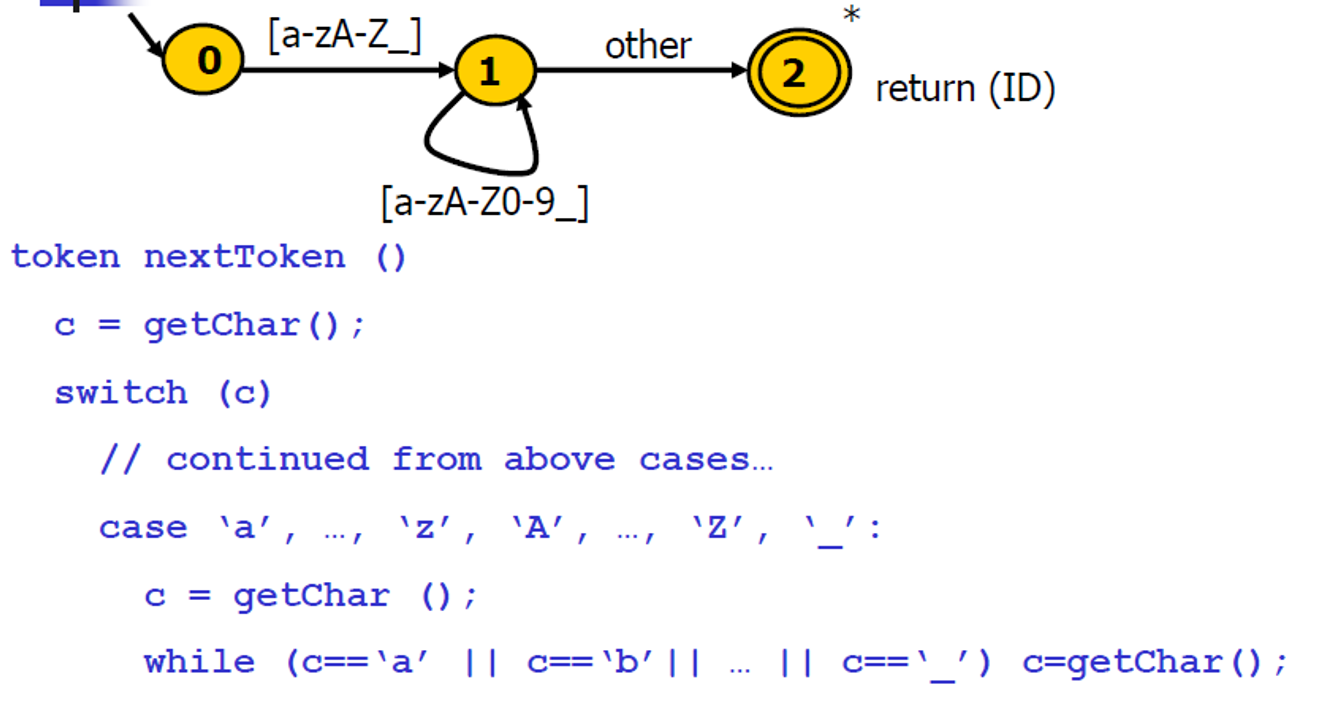
标识符和关键字
- 很多语言中的标识符和关键字有交集
- 从词法分析的角度看,关键字是标识符的一部分
- 以C语言为例:
- 标识符:以字母或下划分开头,后跟零个或多个字母、下划线、或数字
- 关键字:if ,while,else,...
识别关键字(以if为例)
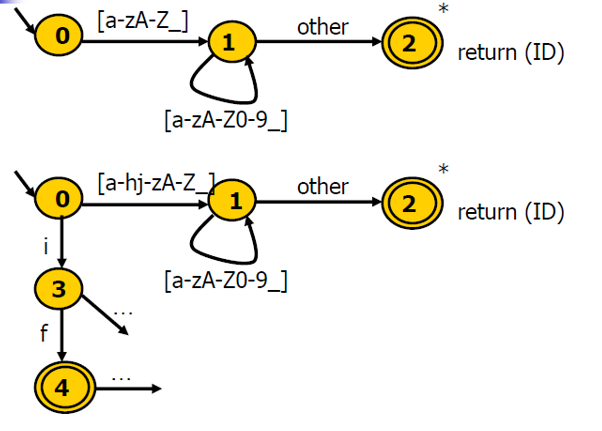
关键字表算法
- 对给定语言中所有的关键字,构造关键字构成的哈希表H
- 对所有的标识符和关键字,先统一按标识符的转移图进行识别
- 识别完成后,进一步查表H看是否是关键字
- 通过合理的构造哈希表(完美哈希),可以在(O(1))时间完成
2.3 正则表达式
自动生成
声明式的规范:正则表达式
转换:正则表达式—>自动机
lex、flex、jlex
正则表达式
- 对给定的字符集(Sigma = { c1,c2,...,cn})
- 归纳定义:
- 空串 (varepsilon) 是正则表达式
- 对于任意(cin Sigma),c是正则表达式
- 如果M和N是正则表达式,则以下也是正则表达式
- 选择 $ M|N = {M,N} $
- 连接 $ MN ={mn| min M,n in N }$
- 闭包 (M*={varepsilon,M,MM,MMM,...})
举例
- 对于给定字符集(Sigma = { a,b}),可以写出哪些正则表达式?
- C语言中的关键字:例如if,while等,如何用正则表达式表示?
- C语言中的标识符:以字母或下划线开头,后跟零个或多个字母、数字或下划线。如何用正则表达式表示?
- C语言中的无符号整数:(十进制整型数)规则:或者是0;或者是以1到9开头,后跟零个或多个0到9。如何用正则表达式表示?
语法糖
- 可以引入更多的语法糖,来简化构造
- [c1-cn] == c1|c2|…|cn
- e+ == 一个或多个 e
- e? == 零个或一个 e
- “a*” == a* 自身, 不是a的Kleen闭包
- e{i, j} == i到j个e的连接
- . == 除‘ ’外的任意字符
2.4 有限状态自动机
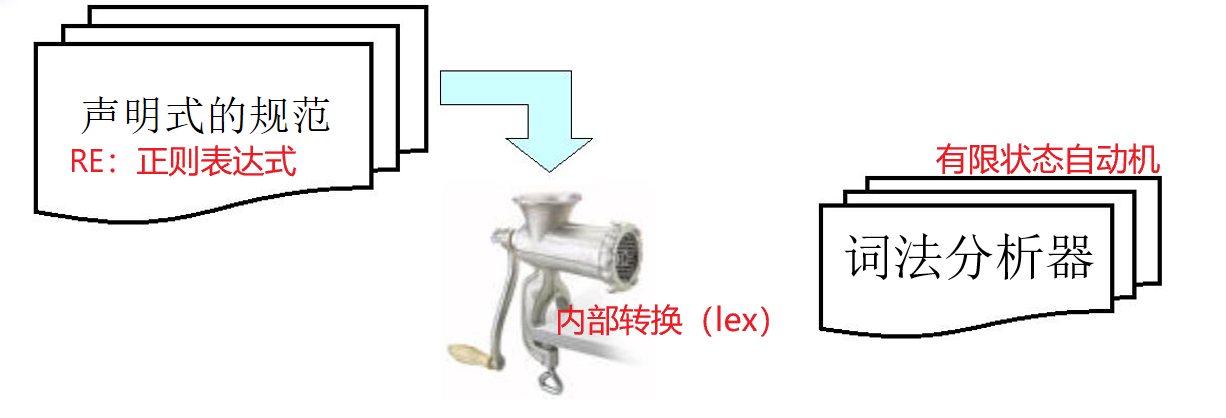
正则表达式(INPUT)、lex(flex)(转换算法内部)、有限状态自动机(OUTPUT)
有限状态自动机(FA)
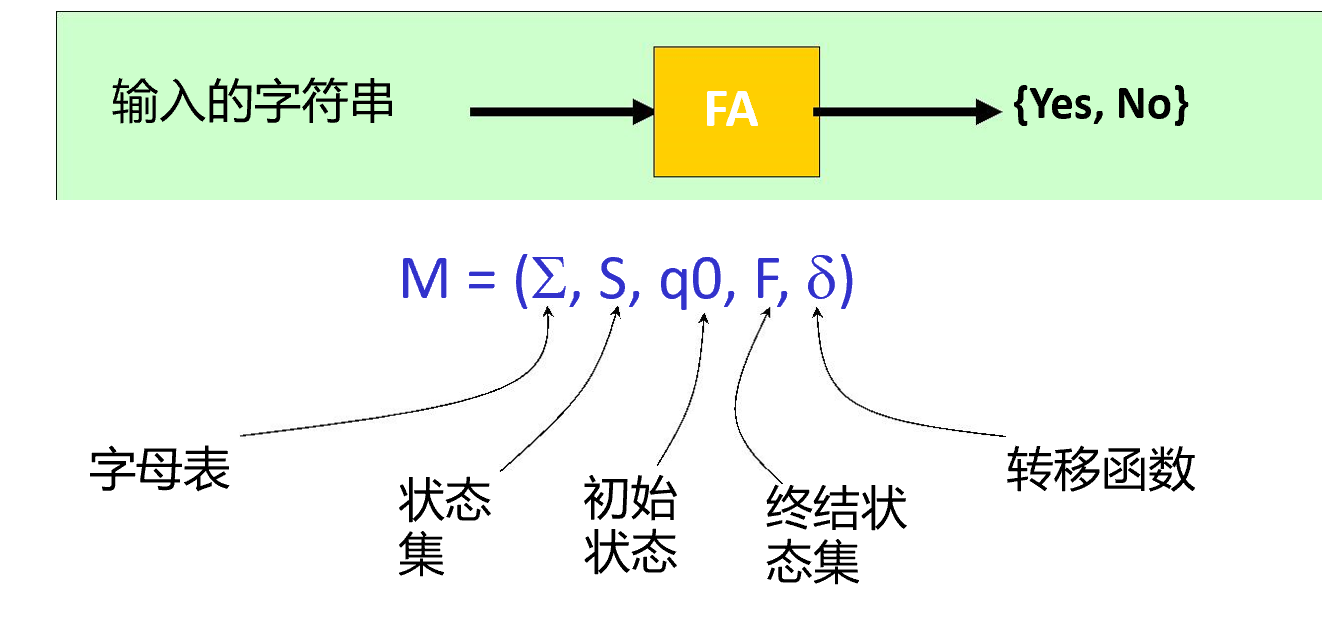
自动机例子1(DFA)
字母表:(Sigma = {a,b})
状态集:(S={0,1,2})
初始状态:(q_0=0)
终结状态集:(F={2})
转移函数:(delta={(q_0, a) ightarrow q_1,(q_0, b) ightarrow q_0,(q_1, a) ightarrow q_2,(q_1, b) ightarrow q_1,(q_2, a) ightarrow q_2,(q_2, b) ightarrow q_2})
实际上转移函数也就是一个映射关系,也可以用如下的图来表示。
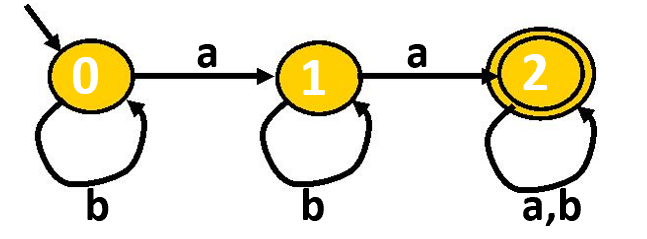
接受:首先处于初始状态,当串S在状态机上读完后转移到了最后状态,即称这个串可以被接受。
自动机例子2(NFA)
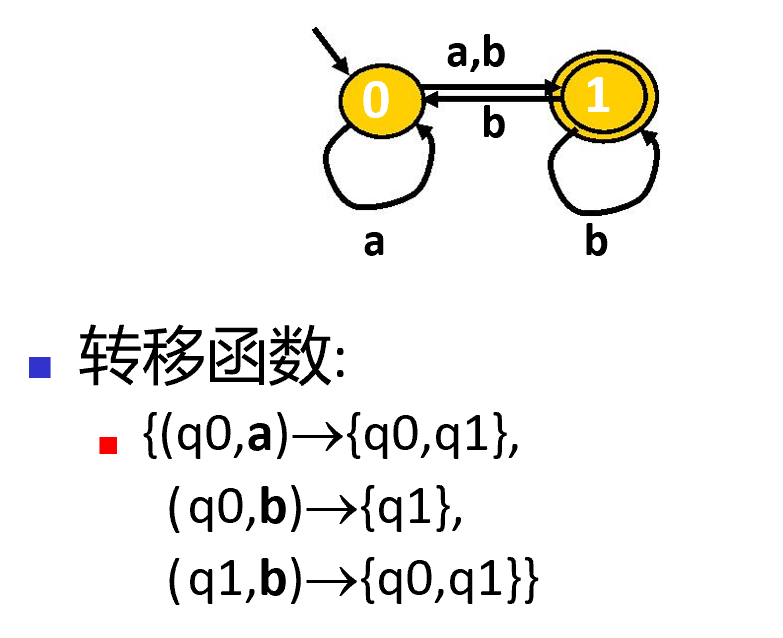
值域发生了变化,转移函数不确定,这类自动机为非确定的自动机(NFA)。上面的例子1就是确定的自动机(DFA)。
对于NFA来说,难以判断是否接受串S。需要遍历,排除不接受的路径,再回溯找到接受的路径。
一般来说,会将NFA转换为DFA来进行简化。
小结
-
确定状态有限自动机DFA
-
对任意的字符,最多有一个状态可以转移
(delta: mathrm{S} imesSigma ightarrow mathrm{S})
(这里是笛卡尔积)
-
-
非确定的有限状态自动机NFA
-
对任意的字符,有多于一个状态可以转移
(delta: mathrm{S} imes(Sigma cup varepsilon) ightarrow wp(mathrm{S}))
(wp(S))表示是幂集
-