搜索算法

搜索是一种有目的地枚举问题的解空间中部分或全部情况，进而找到解的方法。然后，与枚举策略相比，搜索通常是有目的的查找，发现解空间的某一子集内不存在解时，它便会放弃对该子集的搜索，而不像枚举那般逐个地检查子集内的解是否为问题的解。

1.宽度优先搜索

宽度优先搜索策略从搜索的起点开始，不断地优先访问当前结点的邻居。也就是说，首先访问起点，然后依次访问起点尚未访问的邻居结点，再按照访问起点邻居的先后顺序依次访问它们的邻居，直到找到解或搜遍整个解空间。

POJ Catch That Cow

Description

Farmer John has been informed of the location of a fugitive cow and wants to catch her immediately. He starts at a point N (0 ≤ N ≤ 100,000) on a number line and the cow is at a point K (0 ≤ K ≤ 100,000) on the same number line. Farmer John has two modes of transportation: walking and teleporting.

* Walking: FJ can move from any point X to the points X - 1 or X + 1 in a single minute
* Teleporting: FJ can move from any point X to the point 2 × X in a single minute.

If the cow, unaware of its pursuit, does not move at all, how long does it take for Farmer John to retrieve it?

Input

Line 1: Two space-separated integers: N and K

Output

Line 1: The least amount of time, in minutes, it takes for Farmer John to catch the fugitive cow.

Sample Input

5 17

Sample Output

4

Hint

The fastest way for Farmer John to reach the fugitive cow is to move along the following path: 5-10-9-18-17, which takes 4 minutes.

题目大意

分析

代码

#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>

using namespace std;

const int MAXN = 100001;//N和K的范围都是0到100000

struct Status{
    int n,t;//定义当前状态两个参数，位置n，和时间t
    Status(int n,int t):n(n), t(t){}//结构体构造
};

bool visit[MAXN];

int BFS(int n,int k){
    queue<Status> myQueue;
    myQueue.push(Status(n, 0 ));//压入初始状态
    visit[n] = true;//起始点已被访问
    while(!myQueue.empty()){
        Status current = myQueue.front();//取出队列的头作为当前的状态
        myQueue.pop();//出队操作，将队列头删除，即删除当前的状态
        if(current.n == k){
            return current.t;//如果当前状态的n到达了搜索的最终条件，即返回时间t（题目所求的最短时间）
        }
        for (int i = 0; i < 3; ++i) {//题目中涉及到了3种状态转移函数
            Status next(current.n, current.t+1);//初始化下一个状态值（利用结构体构造函数，先初始化为当前的位置，但是时间+1）
            if(i == 0){
                next.n +=1 ;
            }else if(i == 1){
                next.n -= 1;
            }else{
                next.n *=2;
            }
            if(next.n < 0 || next.n >= MAXN || visit[next.n]){
                continue;//判断新状态是否合法以及是否以及被遍历过
            }
            myQueue.push(next);//进队操作，将新状态压入队列中
            visit[next.n] = true;// 将此状态的位置设置为被遍历过
        }
    }

}

int main(){
    int n, k;
    scanf("%d%d",&n,&k);
    memset(visit,false,sizeof(visit));
    printf("%d
",BFS(n,k));
}

POJ Find The Multiple

Description

Given a positive integer n, write a program to find out a nonzero multiple m of n whose decimal representation contains only the digits 0 and 1. You may assume that n is not greater than 200 and there is a corresponding m containing no more than 100 decimal digits.

Input

The input file may contain multiple test cases. Each line contains a value of n (1 <= n <= 200). A line containing a zero terminates the input.

Output

For each value of n in the input print a line containing the corresponding value of m. The decimal representation of m must not contain more than 100 digits. If there are multiple solutions for a given value of n, any one of them is acceptable.

Sample Input

2
6
19
0

Sample Output

10
100100100100100100
111111111111111111

题目大意

分析

代码

#include<iostream>
#include<cstdio>
#include<queue>

using namespace std;

void BFS(int n){
    queue<long long> myQueue;
    myQueue.push(1);//初始状态为1，压入到队列的头
    while(!myQueue.empty()){
        long long current = myQueue.front();
        myQueue.pop();
        if(current % n == 0){
            printf("%lld
",current);
            return;
        }
        myQueue.push(current*10);
        myQueue.push(current*10 + 1);
    }
}
int main(){
    int n;
    while(scanf("%d", &n) != EOF){
        if(n == 0){
            break;
        }
        BFS(n);
    }
    return 0;
}

KY12 玛雅人的密码

题目描述

玛雅人有一种密码，如果字符串中出现连续的2012四个数字就能解开密码。给一个长度为N的字符串，（2=<N<=13）该字符串中只含有0,1,2三种数字，问这个字符串要移位几次才能解开密码，每次只能移动相邻的两个数字。例如02120经过一次移位，可以得到20120,01220,02210,02102，其中20120符合要求，因此输出为1.如果无论移位多少次都解不开密码，输出-1。

输入描述:

输入包含多组测试数据，每组测试数据由两行组成。
第一行为一个整数N，代表字符串的长度（2<=N<=13）。
第二行为一个仅由0、1、2组成的，长度为N的字符串。

输出描述:

对于每组测试数据，若可以解出密码，输出最少的移位次数；否则输出-1。

输入

5
02120

输出

1

代码

#include<iostream>
#include<queue>
#include<string>
using namespace std;
struct mitery{
    int index;//移位次数
    string s;//密码字符串
    mitery(int i,string ss):index(i),s(ss){}
};
void BFS(string s){
    queue<mitery> myQueue;
    myQueue.push(mitery(0,s));//将初始状态压入队列头
    while(!myQueue.empty()){
        mitery current=myQueue.front();
        myQueue.pop();
        string currentString=current.s;
        if(currentString.find("2012")!=string::npos){
            cout<<current.index<<endl;//如果当前字符串以及可以找到2012
            return ;
        }
        for(int i=0;i<currentString.size()-1;i++){//状态转移的方式：每次只能移动相邻的两个数字
            swap(currentString[i],currentString[i+1]);
            myQueue.push(mitery(current.index+1,currentString));
            swap(currentString[i],currentString[i+1]);
        }
    }
    cout<<-1<<endl;
}
int main(){
    int n;
    string s;
    while(cin>>n>>s){
        BFS(s);
    }
    return 0;
}

2.深度优先搜索

搜索过程中，通过放弃对某些不可能产生结果的子集的搜索，达到提高效率的目的。这样的技术被称为剪枝。

POJ A Knight's Journey

Description

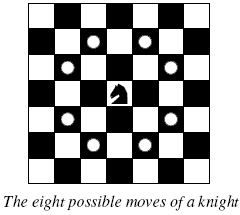
Background
The knight is getting bored of seeing the same black and white squares again and again and has decided to make a journey
around the world. Whenever a knight moves, it is two squares in one direction and one square perpendicular to this. The world of a knight is the chessboard he is living on. Our knight lives on a chessboard that has a smaller area than a regular 8 * 8 board, but it is still rectangular. Can you help this adventurous knight to make travel plans?

Problem
Find a path such that the knight visits every square once. The knight can start and end on any square of the board.

Input

The input begins with a positive integer n in the first line. The following lines contain n test cases. Each test case consists of a single line with two positive integers p and q, such that 1 <= p * q <= 26. This represents a p * q chessboard, where p describes how many different square numbers 1, . . . , p exist, q describes how many different square letters exist. These are the first q letters of the Latin alphabet: A, . . .

Output

The output for every scenario begins with a line containing "Scenario #i:", where i is the number of the scenario starting at 1. Then print a single line containing the lexicographically first path that visits all squares of the chessboard with knight moves followed by an empty line. The path should be given on a single line by concatenating the names of the visited squares. Each square name consists of a capital letter followed by a number.
If no such path exist, you should output impossible on a single line.

Sample Input

3
1 1
2 3
4 3

Sample Output

Scenario #1:
A1

Scenario #2:
impossible

Scenario #3:
A1B3C1A2B4C2A3B1C3A4B2C4

代码

#include<iostream>
#include<cstdio>
#include<string>
#include<cstring>

using namespace std;

const int MAXN = 30;//列数和行数均不超过8（即8×8）的棋盘
int p,q;
bool visit[MAXN][MAXN];
int direction[8][2]{//只能走日字
        {-1,-2},{1,-2},{-2,-1},{2,-1},{-2,1},{2,-1},{-1,2},{1,2}
};
bool DFS(int x,int y,int step,string ans){
    if(step == p*q){//搜索成功
        cout<<ans<<endl<<endl;
        return true;
    }else{
        for (int i = 0; i < 8; ++i) {//遍历邻居节点
            int nx = x + direction[i][0];//计算下一步的状态(x,y)——>(nx,ny)
            int ny = y + direction[i][1];
            char col = ny + 'A';
            char row = nx + '1';//用A-Z来表示列，1-99来表示横行
            if(nx<0||nx>=p||ny<0||ny>=q||visit[nx][ny]){
                continue;//该点不合法或者已经被遍历过
            }
            visit[nx][ny]= true;//标记该点
            if(DFS(nx,ny,step+1,ans+col+row)){
                return true;//递归遍历
            }
            visit[nx][ny]=false;//取消该点
        }
    }
    return false;
}
int main(){
    int n;
    scanf("%d",&n);//第一行中有一个正整数n，代表数据有n组。
    int caseNumber = 0;
    while (n--){
        scanf("%d%d",&p,&q);//对于每组数据，都含有两个正整数p和q(1 <= p * q <= 26)，代表棋盘有p行q列。
        memset(visit,false,sizeof(visit));
        cout<<"Scenrio #"<<++caseNumber<<":"<<endl;
        visit[0][0]=true;//题目要求在所有可行的路径中输出字母表排序最小的那个解，这个解必定经过A1
        if(!DFS(0,0,1,"A1")){//初始状态的坐标是A1（0，0，1，“A1”）
            cout<<"impossible"<<endl<<endl;
        }

    }
}

POJ Square

Description

Given a set of sticks of various lengths, is it possible to join them end-to-end to form a square?

Input

The first line of input contains N, the number of test cases. Each test case begins with an integer 4 <= M <= 20, the number of sticks. M integers follow; each gives the length of a stick - an integer between 1 and 10,000.

Output

For each case, output a line containing "yes" if is is possible to form a square; otherwise output "no".

Sample Input

3
4 1 1 1 1
5 10 20 30 40 50
8 1 7 2 6 4 4 3 5

Sample Output

yes
no
yes

代码

/**
 * 本题剪枝如下：
 * (1)如果总长不能被4整除，则一定不可以构成正方形
 * (2)如果某根木棍的长度大于边长side，那么必定无法构成正方形
 * (3)如果当前木棍无法构成边，之后可以跳过相同的木棍(需要排序)
 */
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>

using namespace std;

const int MAXN = 25;//棍子的个数是4到20
int side;//边长
int m;//木棍数量
int sticks[MAXN];//木棍长度
bool visit[MAXN];

bool DFS(int sum,int number,int position){//sum是当前拼凑的木棍长度，number是当前已经拼凑成的边长数目，position是当前木棍的编号
    if(number==3){//如果总长能够整除4，且已经拼凑出3条边，那么剩下的木棍一定可以构成最后一条边。
        return true;
    }
    int sample=0;//剪枝(3)
    for (int i = position; i < m; ++i) {
        if (visit[i]||sum+sticks[i]>side||sticks[i]==sample){
            continue;//木棍被标记过、超过了边长、木棍之前被放弃过
        }
        visit[i]=true;//标记该木棍
        if(sum+sticks[i]==side){//恰好形成边
            if(DFS(0,number+1,0)){
                return true;
            }else{
                sample=sticks[i];//记录木棍失败长度
            }
        }else{//没有形成边继续拼凑
            if(DFS(sum+sticks[i],number,i+1)){
                return true;
            }else{
                sample=sticks[i];//记录木棍失败长度
            }
        }
        visit[i] = false;
    }
    return false;
}
bool Compare(int x,int y){
    return x>y;
}

int main(){
    int n;
    scanf("%d",&n);//第一行中有一个正整数n，代表数据有n组。
    while(n--){
        int length = 0;//总长
        scanf("%d",&m);//木棍数目
        for (int i = 0; i < m; ++i) {
            scanf("%d",&sticks[i]);//木棍长度
            length += sticks[i];
        }
        memset(visit,false,sizeof(visit));
        if(length%4!=0){//剪枝(1)
            printf("no
");
            continue;
        }
        side = length / 4;//边长
        sort(sticks,sticks+m,Compare);//从大到小排序
        if(sticks[0]>side){//剪枝(2)
            printf("no
");
            continue;
        }
        if(DFS(0,0,0)){//初始状态，第一根木棍开始
            printf("yes
");
        }else{
            printf("no
");
        }
    }
    return 0;
}

KY59 神奇的口袋

题目描述

有一个神奇的口袋，总的容积是40，用这个口袋可以变出一些物品，这些物品的总体积必须是40。John现在有n个想要得到的物品，每个物品的体积分别是a1，a2……an。John可以从这些物品中选择一些，如果选出的物体的总体积是40，那么利用这个神奇的口袋，John就可以得到这些物品。现在的问题是，John有多少种不同的选择物品的方式。

输入描述:

输入的第一行是正整数n (1 <= n <= 20)，表示不同的物品的数目。接下来的n行，每行有一个1到40之间的正整数，分别给出a1，a2……an的值。

输出描述:

输出不同的选择物品的方式的数目。

输入

3
20
20
20

输出

3

代码

法一：递归

/**
 * 法一 ：递归  把物品数目n和物品体积数组a[100]设为全局变量;
 * count(i,sum)表示从数组的第i个数开始往后统计的组合数和为sum的种类数，
 * sum为组合数的和,则：cout(i,sum)=cout(i+1,sum-a[i])+cout(i+1,sum）,
 * 其中cout(i+1,sum-a[i])表示包含了a[i]，即为从第i+1个数开始往后统计
 * 组合数的和为sum-a[i]的种类数, 而cout(i+1,sum）表示不包含a[i]， 即为从第i+1个数开始往后统计组合数的和为sum的种类数 
 */
#include <iostream>
using namespace std;

int a[100];
int n=1;
int count(int i,int sum)
{
    if(sum==0){return 1;} //找到一组和为sum的组合数；
    if(i==n||sum<0) return 0;//i==n说明没有其他的数来组合，sum<0说明组合不出;
    return count(i+1,sum-a[i])+count(i+1,sum);//从数组的第i为开始，包含a[i],和不包含;
}

int main()
{
    while(cin>>n){
        for(int i=0;i<n;i++)
            cin>>a[i];
        cout<<count(0,40)<<endl;
    }
    return 0;
} 

法二：DFS

#include<iostream>
#include<algorithm>
#include<cstring>

using namespace std;
const int MAXN = 25;
const int total = 40; // 总重量
bool visit[MAXN]; // 标记数组
int matter[MAXN]; // 存放物品
int kind = 0; // 记录一共有多少种
int n; // 物品的数量

void DFS(int sum, int position) { // sum为当前已经凑的质量
    if (sum == total) {
        kind++; // 种数增加
        return;
    }
    // 从第一件开始凑数
    for (int i = position; i < n; i++) {
        if (visit[i] || sum + matter[i] > total) {
            continue;
        }
        visit[i] = true;
        DFS(sum + matter[i], i);
        visit[i] = false; // 回溯
    }
}

int main() {
    cin >> n;
    int sum = 0; // 记录所有物品的质量总和
    for (int i = 0; i < n; i++) {
        cin >> matter[i];
        sum += matter[i];
    }
    sort(matter, matter + n);
    // 总和小于40或者最大的已经大于40了
    if (sum < 40 || matter[0] > 40) {
        cout << kind << endl;
        return 0;
    } else {
        memset(visit, false, sizeof(visit));
        DFS(0, 0);
        cout << kind << endl;
    }
    return 0;
}

法三：动态规划

/**
 * 用滚动数组法,每次状态转移仅仅根据前一行数组决定，故选择用一维数组
 * 如果dp[j]已经有了x种方法，而dp[j-volume[i]]也有y种方法
 * 那么由于物体i的存在，对于体积为j的口袋，又能多出dp[j-volume[i]]种方法
 * 例如j=20，volume=10，而有5种方法能装满体积为10的口袋，那么只要有体积为10的物体就一定多出5种装满体积为20的口袋的方法
 * 显而易见，当口袋体积等于该物体体积时，必然有一种方法
 * /而可能不止一个物体有这样的体积，所以每次碰到这个体积的物体，就做一次++运算
 */
#include<cstdio>

int volume[21];//对于所有物品进行遍历，该物体体积为volume[i]
int dp[41];//dp[i]指口袋体积为i时，共有几种方法

int main() {
    int n;
    while (scanf("%d", &n) != EOF) {
        for (int i = 1; i <= n; i++)//输入物品的体积
        {
            scanf("%d", &volume[i]);
        }
        for (int i = 1; i <= n; i++)//对于所有物品进行遍历，该物体体积为volume[i]
        {
            for (int j = 40; j >= volume[i]; j--)//j>=volume[i]因为dp[j]只能从0~40-volume[i]的状态转移而来
            {
                dp[j] += dp[j - volume[i]]; 
            }
            dp[volume[i]]++;
        }             
        printf("%d
", dp[40]);
    }
    return 0;
}

KY86 八皇后

题目描述

会下国际象棋的人都很清楚：皇后可以在横、竖、斜线上不限步数地吃掉其他棋子。如何将8个皇后放在棋盘上（有8 * 8个方格），使它们谁也不能被吃掉！这就是著名的八皇后问题。 对于某个满足要求的8皇后的摆放方法，定义一个皇后串a与之对应，即a=b1b2...b8，其中bi为相应摆法中第i行皇后所处的列数。已经知道8皇后问题一共有92组解（即92个不同的皇后串）。 给出一个数b，要求输出第b个串。串的比较是这样的：皇后串x置于皇后串y之前，当且仅当将x视为整数时比y小。

输入描述:

每组测试数据占1行，包括一个正整数b(1 <= b <= 92)

输出描述:

输出有n行，每行输出对应一个输入。输出应是一个正整数，是对应于b的皇后串。

输入

2
1
92

输出

15863724
84136275

代码

/**
 * 非常朴素的八皇后问题，问题规模也已经框定好了，
 * 只要把每次得到的列号转化成要比较的十进制数字即可
 */

#include<cstdio>
#include<algorithm>
#include<cmath>
#include<vector>

using namespace std;

vector<int> solut;            //用来放最终的结果
int position[9];            //行号从1开始，其中下标代表行号，其中存放的内容代表列号

void DFS(int row)            //row代表要放入的行号,逐行放入，因为要用的是列号，而且按照习惯都是一列一列计算的
{
    if (row == 9)            //row==9意味着从1~8行全都放入,已完成解
    {
        int temp = 0;
        for (int i = 1; i <= 8; i++) {
            temp += position[i] * pow(10, 8 - i);    //非常朴素的计算方法_(:з」∠)_ 
        }
        solut.push_back(temp);                        //把得到的solution放进vector
    } else {
        for (int i = 1; i <= 8; i++) {
            position[row] = i;        //i在这里代表列号
            bool flag = true;        //用一个标志位来标记，是否冲突
            for (int j = 1; j < row; j++) {
                if (position[row] == position[j] || row - position[row] == j - position[j] ||
                    row + position[row] == j + position[j]) {
                    flag = false;
                    break;
                }        //这里的判断条件j - position[j]会把同一主对角线标记为同一个数字，与row - position[row]同时计算就能判断是否冲突
            }
            if (flag)
                DFS(row + 1);
        }
    }
}

int main() {
    DFS(1);                    //直接从第一行开始放
    sort(solut.begin(), solut.end());    //这里应该不用sort因为得到的solution应该都是从小到大
    int n;
    while (scanf("%d", &n) != EOF) {
        printf("%d
", solut[n - 1]);    //因为vector是从0开始的    
    }
    return 0;
}