poj2446Chessboard【矩阵建图+匈牙利】

大意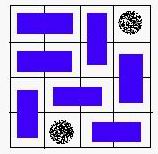： 已知有一个n*m的矩阵现在用1 * 2 的小木块去铺这个矩阵 ，矩阵中的黑点表示陷阱不可以铺，问能不能把除了陷阱之外的所有各自都铺满

nm<= 32

分析：第一印象是状压dp但是n太大，

后来网二分图方向考虑，

首先要构建一个二分图，

怎么构建呢，

我们可以从二分图的定义入手---分成两个部分，并且每个部分内部相互之间不能有边

对于一个矩阵有这么一个现象将每个点坐标的横纵坐标相加，那么和为奇数的点之间肯定不会相连

我们把和为奇数的作为白棋，把和为偶数的作为黑棋

那么用二分图或网络流都可以来做了

代码：

#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;

const int maxn = 33;
const int INF = 1000000000;

struct Node {
    int to;
    int next;
}q[maxn * maxn * 2];

int head[maxn * maxn * 2];
int tot;
int vis[maxn * maxn];
int link[maxn * maxn];

void AddEdge(int u, int v) {
    q[tot].to = v;
    q[tot].next = head[u];
    head[u] = tot ++;
}

int x_cnt;
int X[maxn * maxn];

bool find(int u) {
    for(int i = head[u]; i; i = q[i].next) {
        int v = q[i].to;
        if(!vis[v]) {
            vis[v] = 1;
            if(link[v] == -1 || find(link[v])) {
                link[v] = u;
                return true;
            }
        }
    }
    return false;
}

int KM() {
    int num = 0;
    memset(link, -1, sizeof(link));
    for(int i = 0; i < x_cnt; i++) {
        memset(vis, 0, sizeof(vis));
        if(find(X[i])) num++;
    }
    return num;
}

bool mat[maxn][maxn];

int xx[4] = {0, 0, 1, -1};
int yy[4] = {1, -1, 0, 0};

int n, m;

int change(int i, int j) {
    return m * (i - 1) + j;
}

bool check(int i, int j) {
    if(i >= 1 && i <= n && j >= 1 && j <= m && mat[i][j] == false) return true;
    return false;
}

int main() {
    int k; int x, y;
    //freopen("2446.txt","r",stdin);
    while(EOF != scanf("%d %d %d",&n, &m, &k)) {
        //if(n * m - k)
        int ans_cnt = n * m - k;
        if(ans_cnt & 1) {puts("NO"); continue;}
        ans_cnt /= 2;
        memset(mat, false, sizeof(mat));
        for(int i = 0; i < k; i++) {
            scanf("%d %d",&x, &y);
            mat[y][x] = true;
        }
        x_cnt = 0;
        tot = 1; memset(head, 0, sizeof(head));
        for(int i = 1; i <= n; i++) {
            for(int j = 1; j <= m; j++) {
                if(!mat[i][j] && (i + j) % 2 == 1) {
                    int num_x = change(i, j);
                    X[x_cnt++] = num_x;
                    for(int k = 0; k < 4; k++) {
                        int tmpx = i + xx[k]; int tmpy = j + yy[k];
                        if(!check(tmpx, tmpy)) continue;
                        int num_y = change(tmpx, tmpy);
                        AddEdge(num_x, num_y);
                    }
                }
            }
        }
        int ans = KM();
        if(ans == ans_cnt) puts("YES");
        else puts("NO");
    }
    return 0;
}