力扣98题，700题，701题，450题、669（二叉搜索树，递归）

98.验证二叉搜索树

具体实现：

 

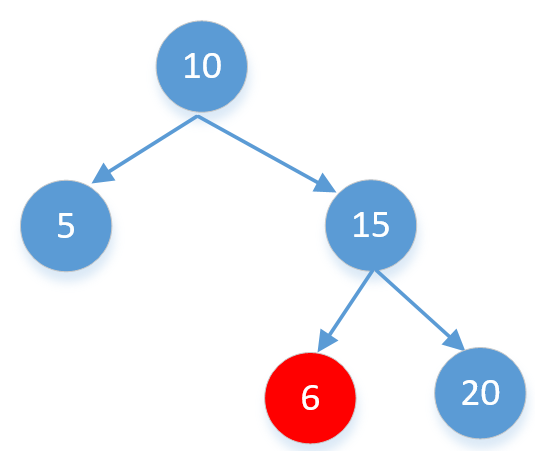
注意6这个节点不光要小于15而且还要大于10，所以这里的每一个节点都是有一个范围的，下面代码只判断了6比15小，但没有和10进行比较，所以代码是错误的。

class Solution:
    def isValidBST(self,root):
         if not node:
            return Ture;
        if root.val <=  root.left.val:return Fasle
        if root.val >=  root.right.val:return Fasle
        return   self.isValidBST(root.left) && self.isValidBST(root.right)

递归三步

1、确定递归参数以及返回值

参数：根节点

返回值：

遍历整棵树不需要返回值，寻找一条边或者一个节点需要返回值

这道题在寻找一个不符合条件的节点，

如果没有找到这个节点就遍历了整棵树，如果找到不符合条件的节点就立刻返回

2、结束条件

二叉树为空节点

3、单层递归逻辑

中序遍历，验证遍历的元素是不是从小到大

prev记录前一个节点

代码：

中序遍历：

class Solution {
    private long prev = Long.MIN_VALUE;
    public boolean isValidBST(TreeNode root) {
        if (root == null) {
            return true;
        }
        if (!isValidBST(root.left)) {
            return false;
        }
        if (root.val <= prev) { // 不满足二叉搜索树条件
            return false;
        }
        prev = root.val;
        return isValidBST(root.right);
    }
}

 迭代法：

class Solution {
    public boolean isValidBST(TreeNode root) {
       if (root == null) return true;
       Stack<TreeNode> stack = new Stack<>();
       TreeNode pre = null;
       while (root != null || !stack.isEmpty()){
           while (root != null){
               stack.push(root);
               root = root.left;
           }
           TreeNode pop = stack.pop();
           if (pre != null && pop.val <= pre.val) return false;
           pre = pop;
           root = pop.right;
       }
       return true;
    }
}

递归：

给每个节点添加一个范围，如果不在这个范围之内直接返回false，比如6这个位置的节点的范围应该是(10,15)，

很明显他不在这个范围内，所以他不是二叉搜索树。

a.函数递归调用的入口为validBST(Long.MIN_VALUE,Long.MAX_VALUE,root)

b.整棵左子树和右子树进行比较

递归调用左子树时，上界upper改为root.val，即调用validBST(lower, root.val,root.left)

左子树里所有节点的值都小于它的根节点的值

递归调用右子树时，下界lower改为root.val，即调用validBST(root.val,upper,root.right)

右子树里所有节点的值都大于它的根节点的值

class Solution {
    public boolean isValidBST(TreeNode root) {
        return validBST(Long.MIN_VALUE,Long.MAX_VALUE,root);
    }
    boolean validBST(long lower, long upper, TreeNode root){
        if (root == null) return true;
        if (root.val <= lower || root.val >= upper) return false;
        return validBST(lower, root.val,root.left) && validBST(root.val,upper,root.right);

    }
}

 700.二叉搜索树中的搜索

基本思想：

利用二叉搜索树的特点，左小右大。类似于二分查找法

具体实现：

用要查找的数和节点数作比较，比较完可以排除另一边

代码：

class Solution:
    def searchBST(self, root: TreeNode, val: int) -> TreeNode:
        if root is None or val == root.val:
            return root
        
        if root.val < val:
            return self.searchBST(root.right, val)
        if root.val > val:
            return self.searchBST(root.left, val)

class Solution {
    // 递归，利用二叉搜索树特点，优化
    public TreeNode searchBST(TreeNode root, int val) {
        if (root == null || root.val == val) return root;
        if (val < root.val) return searchBST(root.left, val);
        else return searchBST(root.right, val);
    }
}

迭代法

class Solution {
    
    public TreeNode searchBST(TreeNode root, int val) {
        while (root != null)
            if (root.val >val) root = root.left;
            else if (root.val < val) root = root.right;
            else return root;
        
        return null;
    }
}

 701.在BST中插入一个数

 基本思想：

在BST中插入一个数的位置不唯一，只要还是BST就好。

涉及到改。函数就要返回整棵树，并且对递归调用的返回值进行接收。

 具体实现：

 （1）节点不存在，找到空位置插入新节点

if not root:return TreeNode(val)

（2）如果节点已经存在，不需要重复插入，直接返回

if root.val==val:return root

（3）val大，插入右子树

if root.val<val:root.right = insertIntoBST(root.right,val)

（4）val小，插入左子树

if root.val>val:root.right = insertIntoBST(root.left,val)

(5)返回整棵数

return root

递归三步：

1、确定递归函数参数以及返回值

参数：根节点，要插入的元素

返回值：返回节点类型为TreeNode

2、确定终止条件

找到遍历的节点为null时，就是要插入节点的位置了，并把插入的节点返回

if not root:
            return TreeNode(val)

这里把返回的节点给上一层，就完成了父子节点的赋值操作

3、确定单层递归的逻辑

if root.val < val:
            root.right = self.insertIntoBST(root.right, val)
        else:
            root.left = self.insertIntoBST(root.left, val)

下一层将加入节点返回，本层用root.left或者root.right接住

代码：

class Solution:
    def insertIntoBST(self, root: TreeNode, val: int) -> TreeNode:
        if not root:
            return TreeNode(val)
        if root.val == val:
            return root
        if root.val < val:
            root.right = self.insertIntoBST(root.right, val)
        else:
            root.left = self.insertIntoBST(root.left, val)
        return root

递归没有返回值的解法

找到插入的节点位置，直接让父节点指向插入节点，结束递归

没有返回值，需要记录上一个节点，遇到空节点，就让parent左孩子或右孩子指向新插入的节点

class Solution {
    TreeNode parent = new TreeNode(0);
    public TreeNode insertIntoBST(TreeNode root, int val) {
        if (root == null) root = new TreeNode(val);
        traversal(root, val);
        return root;
    }

    public void traversal(TreeNode cur, int val){
        if (cur == null){
            TreeNode node = new TreeNode(val);
            if (val > parent.val) {
                parent.right = node;
            } else {
                parent.left = node;
            }
            return;
        }
        parent = cur;
        if (cur.val > val) traversal(cur.left, val);
        if (cur.val < val) traversal(cur.right, val);
        return;
    }
}

迭代法

class Solution {
    public TreeNode insertIntoBST(TreeNode root, int val) {
        if (root == null) return new TreeNode(val);
        TreeNode newRoot = root;
        TreeNode pre = root;
        while (root != null){
            pre = root;
            if (root.val > val){
                root = root.left;
            } else if (root.val < val) {
                root = root.right;
            }
        }

        if (pre.val > val) {
            pre.left = new TreeNode(val);
        } else {
            pre.right = new TreeNode(val);
        }

        return newRoot;
    }
}

 450.删除BST中的一个数

 基本思想：

删除节点的同时不能破坏BST的性质，分类讨论。

基本框架要会写出来

具体实现：

递归三步：

1、递归参数以及返回值

参数：根节点，要删除的值

返回值：返回值类型为TreeNode

2、确定终止条件

遍历到空节点返回root

3、确定单层递归的逻辑

找不到删除的节点，遍历到空节点直接返回

找到删除的节点：

（1）要删除的节点是叶子节点，左右孩子都为空，直接删除节点，返回null为根节点

代码中（1）和（2）合体了，因为这个删除的节点没有孩子，（2）是没有左孩子，返回右孩子，（1）也返回右孩子，但是（1）的右孩子为null

（2）要删除的节点没有左孩子，有右孩子，删除节点，右孩子补位，返回右孩子为根节点

（3）要删除的节点没有右孩子，有左孩子，删除节点，左孩子补位，返回左孩子为根节点

（4） 要删除的节点左右孩子都在，将删除节点的左子树放到删除节点的右子树的最左面节点的左孩子上，返回删除节点的右孩子为新的节点

 （4）的第二种方法：

要删除的节点找到左子树中最大的那个节点，或者右子树中最小的的那个节点接替自己

这里举例第二种方式，在右子树中找到最小的节点接替自己

 

代码：

第一种方法

class Solution {
    public TreeNode deleteNode(TreeNode root, int key) {
        if (root == null) return null;
        if (root.val > key) root.left = deleteNode(root.left, key);
        else if (root.val < key) root.right = deleteNode(root.right, key);
        else {
            if (root.left == null) return root.right;
            if (root.right == null) return root.left;
            TreeNode tmp = root.right;
            while (tmp.left != null){
                tmp = tmp.left;
            }//找到了要删除节点的右子树的最左节点，赋给tmp
            tmp.left = root.left; //要删除节点的左子树接到右子树的最左节点下面
            root = root.right ;
            //将要删除节点的右子树接替要删除节点
        }
        return root;
    }
}

第二种方法

class Solution {
    public TreeNode deleteNode(TreeNode root, int key) {
        if (root == null) return null;
        if (root.val > key) root.left = deleteNode(root.left, key);
        else if (root.val < key) root.right = deleteNode(root.right, key);
        else {
            if (root.left == null) return root.right;
            if (root.right == null) return root.left;
            TreeNode tmp = root.right;
            while (tmp.left != null){
                tmp = tmp.left;
            }//找到了要删除节点的右子树的最左节点，赋给tmp
            root.val = tmp.val; //将tmp的值给要删除节点
            root.right = deleteNode(root.right,tmp.val);
            //在要删除节点的右子树中再删除掉他的最左节点
        }
        return root;
    }
}

669、修剪二叉搜索树

基本思想：

发现不符合要求的节点，将节点的孩子给这个节点的父节点

具体实现：

1、确定递归参数以及返回值

参数：根节点

返回值：遍历整棵树做修改，可以不需要返回值

　　　　但是有返回值更方便，可以通过递归函数的返回值来移除节点

2、确定终止条件

遇到空节点返回

3、单层递归逻辑

如果root（当前节点）的元素小于low的数值，那么应该递归右子树，并返回右子树符合条件的头结点。

 if (root.val < low) {
            return trimBST(root.right, low, high);// 寻找符合区间[low, high]的节点

}

如果root(当前节点)的元素大于high的，那么应该递归左子树，并返回左子树符合条件的头结点。

if (root.val > high) {
            return trimBST(root.left, low, high);// 寻找符合区间[low, high]的节点

}

接下来要将下一层处理完左子树的结果赋给root.left，处理完右子树的结果赋给root.right。

root.left = trimBST(root.left, low, high);// root->left接入符合条件的左孩子

 root.right = trimBST(root.right, low, high); // root->right接入符合条件的右孩子

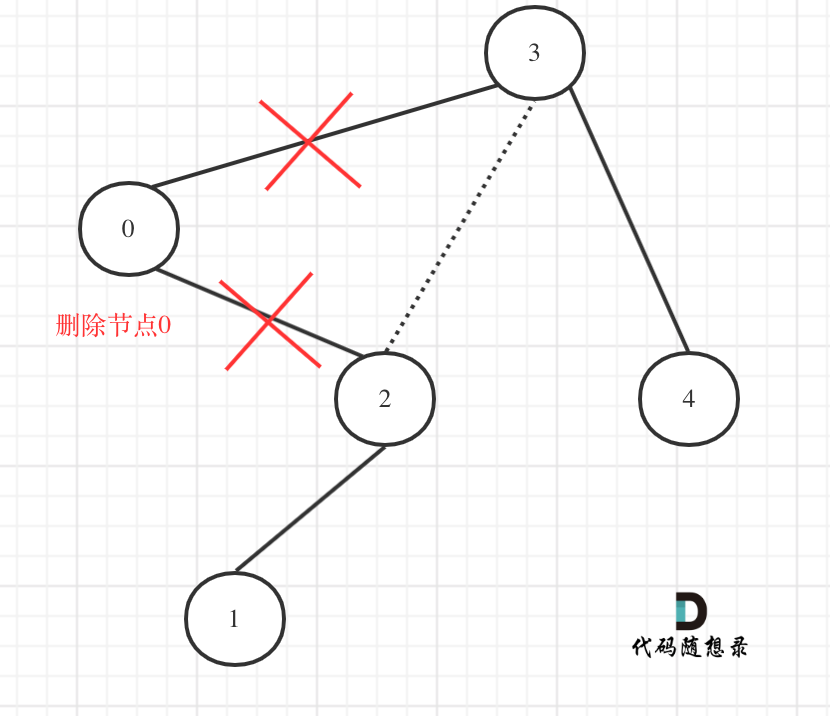
删除节点0

（1）把节点0的右孩子（节点2），返回给上一层

 if (root.val < low) {
            return trimBST(root.right, low, high);// 寻找符合区间[low, high]的节点

}

 （2）用节点3的左孩子把下一层的节点0的右孩子（节点2）接住

root.left = trimBST(root.left, low, high);// root.left接入符合条件的左孩子

代码：

class Solution {
    public TreeNode trimBST(TreeNode root, int low, int high) {
        if (root == null) return null;
        if (root.val < low) return trimBST(root.right, low, high);
        if (root.val > high) return trimBST(root.left, low, high);
         root.left = trimBST(root.left, low, high);
         root.right = trimBST(root.right, low, high);
         return root;
    }
}