力扣513题、112题、113题（找树左下角的值，路径总和）

513、找树左下角的值

基本思想：

树的最后一行找到最左边的值

树的最后一行：深度最大的叶子节点---前序遍历

最左边：优先左边搜索---前序遍历

具体实现：

1、确定递归参数和返回值

参数：根节点和int型变量记录深度

返回值：不需要

如果要遍历整棵树，递归函数不能有返回值

如果要遍历某一条固定路线，递归函数就一定要返回值

本题要遍历整个树找到最深的叶子节点，需要遍历整棵树，所以没有返回值

2、终止条件

遇到叶子节点，统计一下最大的深度了，所以需要遇到叶子节点来更新最大深度maxLen。

if (root.left == null && root.right == null){
       if (leftLen > maxLen) {
             maxLen = leftLen;
             maxLeftValue = root.val;
        }
        return;
 }

3、单层递归逻辑

回溯

代码：

class Solution {
    private int maxLen = -1;
    private int maxLeftValue = 0;
    public int findBottomLeftValue(TreeNode root) {
        findLeftValue(root,0);
        return maxLeftValue;
    }
    private void findLeftValue (TreeNode root, int leftLen){
        if (root == null) return;
        if (root.left == null && root.right == null){
            if (leftLen > maxLen) {
                maxLen = leftLen;
                maxLeftValue = root.val;
            }
            return;
        }

        if (root.left != null){
            leftLen++;
            findLeftValue(root.left,leftLen);
            leftLen--;
        }

        if(root.right != null){
            leftLen++;
            findLeftValue(root.right,leftLen);
            leftLen--;
        }
        return;
    }
}

迭代法

class Solution {

    public int findBottomLeftValue(TreeNode root) {
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        int res = 0;
        while (!queue.isEmpty()) {
            int size = queue.size();
            for (int i = 0; i < size; i++) {
                TreeNode poll = queue.poll();
                if (i == 0) {
                    res = poll.val;
                }
                if (poll.left != null) {
                    queue.offer(poll.left);
                }
                if (poll.right != null) {
                    queue.offer(poll.right);
                }
            }
        }
        return res;
    }
}

112、路径总和

基本思想：

前中后序遍历都可以

具体实现：

1、确定递归参数以及返回值

递归参数：根节点，计数器（用于计算二叉树的一条边是否正好是目标和）

返回值：搜索其中一条符合条件的路径，需要返回值

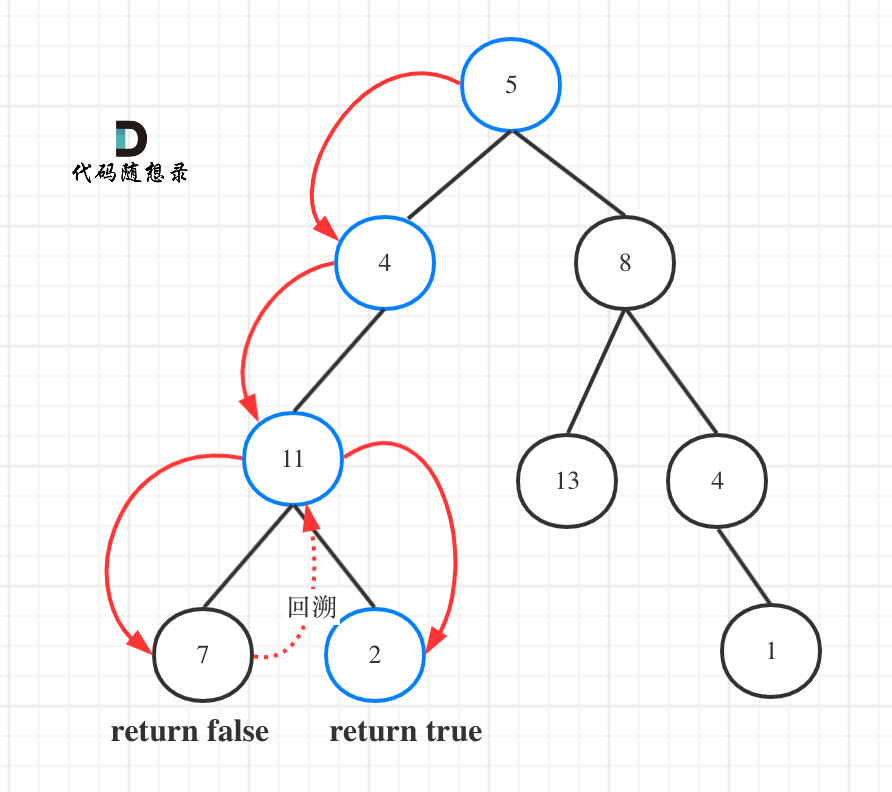
从遍历的路线看出，不需要遍历整棵树，所以递归函数需要返回值，用布尔类型

2、确定终止条件

计数器count初始化为目标和

然后每次减去遍历路径节点上的数值

如果count==0，同时到了叶子节点，说明找到了目标节点

如果到了叶子节点，count不为0，说明没找到

3、单层递归逻辑

回溯

代码：

class Solution {
    public boolean hasPathSum(TreeNode root, int targetSum) {
        if (root == null) {
            return false;
        }
        return traversal(root, targetSum - (root.val));
    }

    private boolean traversal(TreeNode root, int count){
        if (root.left == null && root.right == null && count == 0) return true;
        if (root.left == null && root.right == null) return false;
        if (root.left != null) {
            count -= root.left.val;
            if (traversal(root.left, count)) return true;
            count += root.left.val;
        }
        if (root.right != null) {
            count -= root.right.val;
            if (traversal(root.right, count)) return true;
            count += root.right.val;
        }
        return false;
        
    }
}

迭代法

class Solution {
    public boolean hasPathSum(TreeNode root, int targetSum) {
        if (root == null) {
            return false;
        }
        Stack<TreeNode> stack1 = new Stack<>();
        Stack<Integer> stack2 = new Stack<>();
        stack1.push(root);
        stack2.push(root.val);
        while (!stack1.isEmpty()){
            int size = stack1.size();
            for (int i = 0; i < size; i++){
                TreeNode node = stack1.pop();
                int sum = stack2.pop();
                // 如果该节点是叶子节点了，同时该节点的路径数值等于sum，那么就返回true
                if (node.left == null && node.right == null && sum == targetSum) return true;
                // 右节点，压进去一个节点的时候，将该节点的路径数值也记录下来
                if (node.right != null) {
                    stack1.push(node.right);
                    stack2.push(sum+node.right.val);
                }
                // 左节点，压进去一个节点的时候，将该节点的路径数值也记录下来
                if (node.left != null) {
                    stack1.push(node.left);
                    stack2.push(sum+node.left.val);
                }
            }
        }
        return false;
    }
}

113、路径总和ii

基本思想：

具体实现：

返回值：不需要，因为要遍历整个树

代码：

class Solution {
    public List<List<Integer>> pathSum(TreeNode root, int targetSum) {
        List<List<Integer>> res = new ArrayList<>();
        if (root == null) return res;
        List<Integer> path = new LinkedList<>();
        preorderdfs(root, targetSum, res, path);
        return res;
    }

    public void preorderdfs(TreeNode root, int targetSum, List<List<Integer>> res, List<Integer> path){
        path.add(root.val);
        if (root.left == null && root.right == null){
            if (root.left == null && root.right == null){
                if(targetSum - root.val == 0){
                    res.add(new ArrayList<>(path));
                }
            }
            return;
        }

        if (root.left != null){
            preorderdfs(root.left, targetSum - root.val, res, path);
            path.remove(path.size() - 1);
        }

        if (root.right != null){
            preorderdfs(root.right, targetSum - root.val, res, path);
            path.remove(path.size() - 1);
        }
    }
}