力扣392题、115题、583题、72题（编辑距离）

392、判断子序列

基本思想：

动态规划

具体实现：

1.确定dp数组含义

dp[i][j] 表示以下标i-1为结尾的字符串s，和以下标j-1为结尾的字符串t，相同子序列的长度为dp[i][j]。

2.确定递推公式

两种情况

• if (s[i - 1] == t[j - 1])
  • t中找到了一个字符在s中也出现了，dp[i][j] = dp[i - 1][j - 1] + 1;
• if (s[i - 1] != t[j - 1])
  • 相当于t要删除元素，继续匹配，t如果把当前元素t[j - 1]删除，那么dp[i][j] 的数值就是 看s[i - 1]与 t[j - 2]的比较结果了
  • dp[i][j] = dp[i][j - 1]

3.dp数组如何初始化

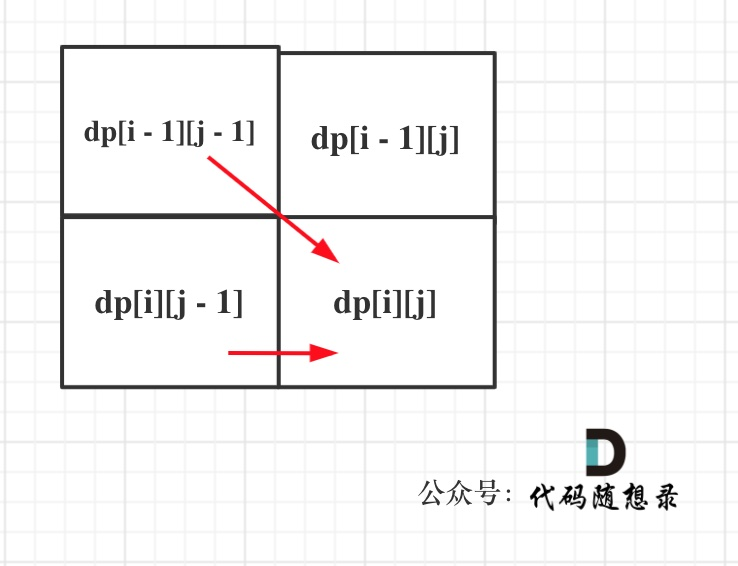
从递推公式可以看出dp[i][j]都是依赖于dp[i - 1][j - 1] 和 dp[i][j - 1]，所以要初始化dp[0][0]和dp[i][0]

根据定义推出dp[i][0]和dp[0][j]是没有含义的，所以初始化为0

4.确定遍历顺序

从递推公式可以看出dp[i][j]都是依赖于dp[i - 1][j - 1] 和 dp[i][j - 1]，那么遍历顺序也应该是从上到下，从左到右

5.举例

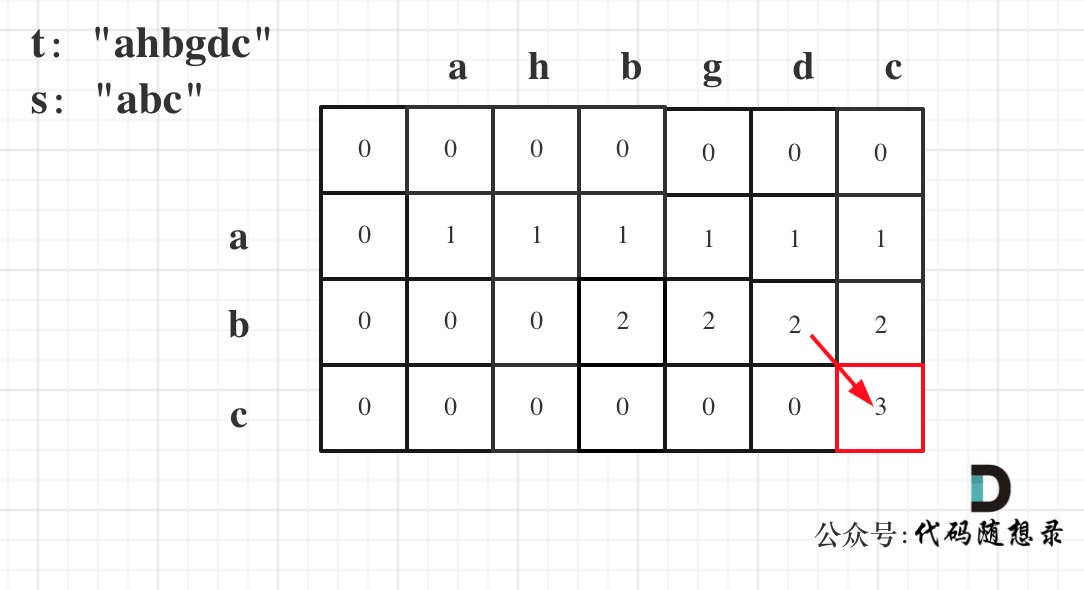
代码:

class Solution {
    public boolean isSubsequence(String s, String t) {
        int length1 = s.length();
        int length2 = t.length();
        int[][] dp = new int[length1+1][length2+1];
        for(int i = 1; i <= length1; i++){
            for(int j = 1; j <= length2; j++){
                if(s.charAt(i - 1) == t.charAt(j - 1)){
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                } else {
                    dp[i][j] = dp[i][j - 1];
                }
            }
        }
        if(dp[length1][length2] == length1){
            return true;
        } else {
            return false;
        }
    }
}

115、不同的子序列

基本思想：

动态规划

具体实现：

1.确定dp数组（dp table）以及下标的含义

dp[i][j]：以i-1为结尾的s子序列（s子序列里有i个字符）中出现以j-1为结尾的t子序列（t子序列中有j个字符）的个数为dp[i][j]

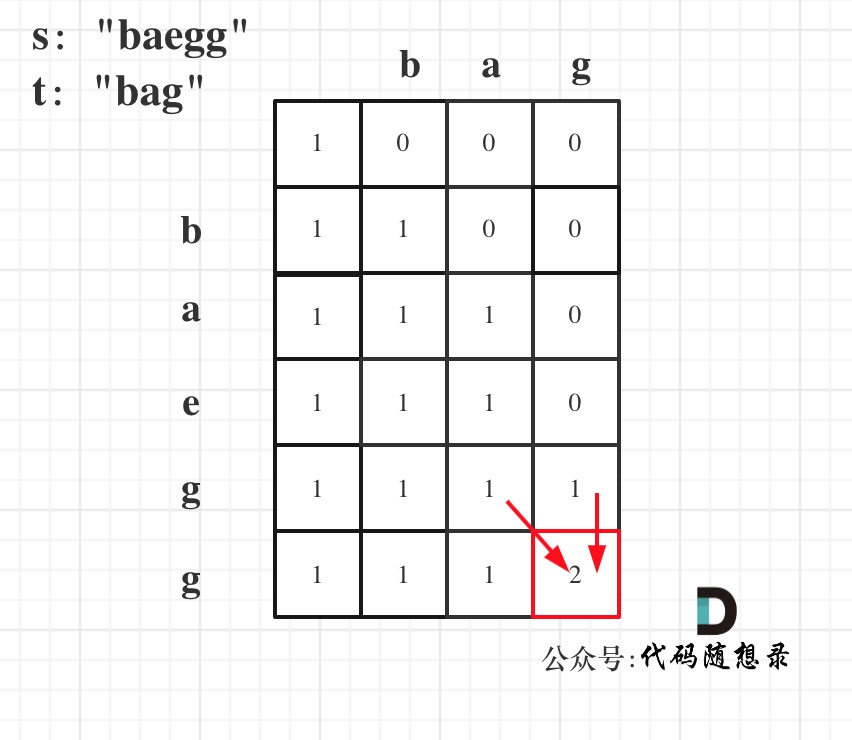
2.确定递推公式s：bagg 和 t：bag，i=4.j=3

• s[i-1]=t[j-1]，s[3] =t[2]，dp[i][j]有两部分组成，dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j]; 
  • 用s[i-1]来匹配，让 s 中 [0,i-1]个字符（bagg）去匹配 t 中的 [0,j−1] 字符（bag）
    • 因为s[i-1]=t[j-1]，s[3] =t[2]，所以个数为s[0到i-2]和t[0到j-2]匹配结果dp[i - 1][j - 1]。去匹配bag和ba，s 中 [0,i-2]，t 中的 [0,j−2]
    • 用s[3]来匹配，即：s[0]s[1]s[3]组成的bag。
  • 一部分是不用s[i - 1]来匹配，让 s 中 [0,i-2] （bag）个字符去匹配 t 中的 [0,j-1]字符（bag），
    • 个数为dp[i - 1][j]。字符串s不用s[3]来匹配，即用s[0]s[1]s[2]组成的bag。

• s[i]！=t[j]dp[i][j]只有一部分组成，dp[i - 1][j]
• • 不用s[i ]来匹配，即：dp[i - 1][j]

3.初始化

dp[i][0] 表示：以i-1为结尾的s可以随便删除元素，出现空字符串的个数。

dp[i][0]都是1，因为也就是把以i-1为结尾的s，删除所有元素，出现空字符串的个数就是1。

dp[0][j]：空字符串s可以随便删除元素，出现以j-1为结尾的字符串t的个数。

dp[0][j]都是0，s如论如何也变成不了t。

dp[0][0]=1，空字符串s，可以删除0个元素，变成空字符串t。

代码：

class Solution {
    public int numDistinct(String s, String t) {
        int[][] dp = new int[s.length() + 1][t.length() + 1];
        for (int i = 0; i < s.length() + 1; i++) {
            dp[i][0] = 1;
        }
        
        for (int i = 1; i < s.length() + 1; i++) {
            for (int j = 1; j < t.length() + 1; j++) {
                if (s.charAt(i - 1) == t.charAt(j - 1)) {
                    dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
                }else{
                    dp[i][j] = dp[i - 1][j];
                }
            }
        }
        
        return dp[s.length()][t.length()];
    }
}

583、两个字符串的删除操作

基本思想：

与上一题不同的地方是两个字符串都可以删除

具体实现：

1.确定dp数组以及下标的含义

dp[i][j]：以i-1为结尾的字符串word1，和以j-1位结尾的字符串word2，想要达到相等，所需要删除元素的最少次数。

2.确定递推公式

（1）当word1[i - 1] 与 word2[j - 1]相同的时候，dp[i][j] = dp[i - 1][j - 1];

（2）当word1[i - 1] 与 word2[j - 1]不相同的时候，有三种情况：

　　情况1：删word1[i - 1]，最少操作次数为dp[i - 1][j] + 1

　　情况2：删word2[j - 1]，最少操作次数为dp[i][j - 1] + 1

　　情况3：同时删word1[i - 1]和word2[j - 1]，操作的最少次数为dp[i - 1][j - 1] + 2

　　取最小值dp[i][j] = min({dp[i - 1][j - 1] + 2, dp[i - 1][j] + 1, dp[i][j - 1] + 1});

3.dp数组如何初始化

dp[i][0]：word2为空字符串，以i-1为结尾的字符串word1要删除多少个元素，才能和word2相同，

所以dp[i][0] = i。

dp[0][j]同理

4.确定遍历顺序

从上到下，从左到右

5.举例推导dp数组

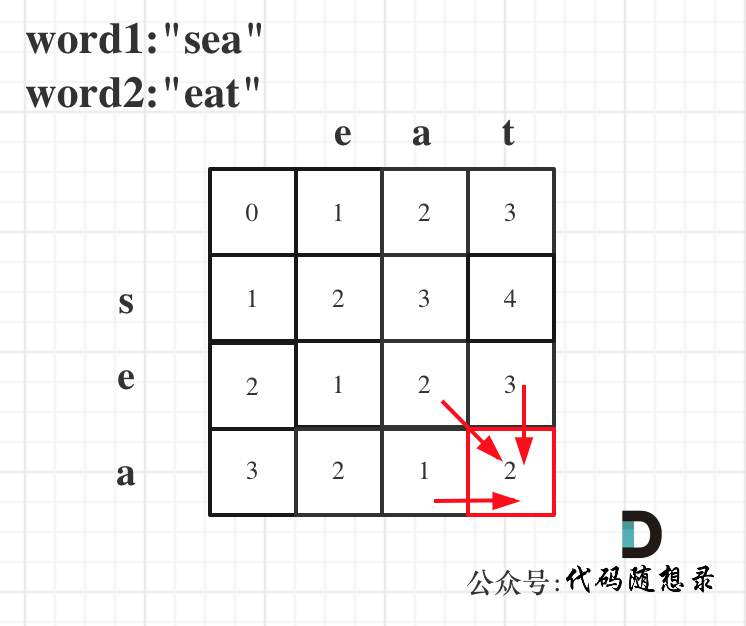
代码：

class Solution {
    public int minDistance(String word1, String word2) {
        int[][] dp = new int[word1.length() + 1][word2.length() + 1];
        for (int i = 0; i < word1.length() + 1; i++) dp[i][0] = i;
        for (int j = 0; j < word2.length() + 1; j++) dp[0][j] = j;
        for (int i = 1; i < word1.length() + 1; i++) {
            for (int j = 1; j < word2.length() + 1; j++) {
                if (word1.charAt(i - 1) == word2.charAt(j - 1)) {
                    dp[i][j] = dp[i - 1][j - 1];
                } else {
                    dp[i][j] = Math.min(dp[i - 1][j - 1] + 2,Math.min(dp[i - 1][j] + 1, dp[i][j - 1] + 1));
                }
            }
        }
        return dp[word1.length()][word2.length()];
    }
}

72、编辑距离

基本思想：

动态规划

具体实现：

1.确定dp数组以及下标的含义

dp[i][j] 表示以下标i-1为结尾的字符串word1，和以下标j-1为结尾的字符串word2，最近编辑距离为dp[i][j]。

2.确定递推公式

A.  word1[i - 1] == word2[j - 1]

不用任何编辑，dp[i][j] = dp[i - 1][j - 1];

B.  word1[i - 1] != word2[j - 1]

（1）word1删除一个元素

以下标i - 2为结尾的word1 与 j-1为结尾的word2的最近编辑距离 再加上一个操作。

举例：

                  i-2  i-1                      j-1

word1 = ab c    d        word2=abc

（2）word2删除一个元素

以下标i - 1为结尾的word1 与 j-2为结尾的word2的最近编辑距离 再加上一个操作。

word2删除一个元素相当于word1添加一个元素

                  i-1                       j-2 j-1

word1 = ab c         word2=abc   d

word1为"abc"，word2为"abcd"，

他俩变得一样的话word2删除一个d的操作和word1添加一个操作数一样

（3）替换元素

word1替换word1[i-1]，使其与word2[j - 1]相同，此时不用增加元素

以下标i - 2为结尾的word1 与 j-2为结尾的word2的最近编辑距离 再加上一个操作。

                 i-2   i-1                 j-2  j-1

word1 = abc    s     word2=abc   d

3.dp数组如何初始化

 dp[i][0] ：以下标i-1为结尾的字符串word1，和空字符串word2，最近编辑距离为dp[i][0]。

dp[i][0]就应该是i，对word1里的元素全部做删除操作，即：dp[i][0] = i;

同理dp[0][j] = j;

4.遍历顺序

从左到右，从上到下

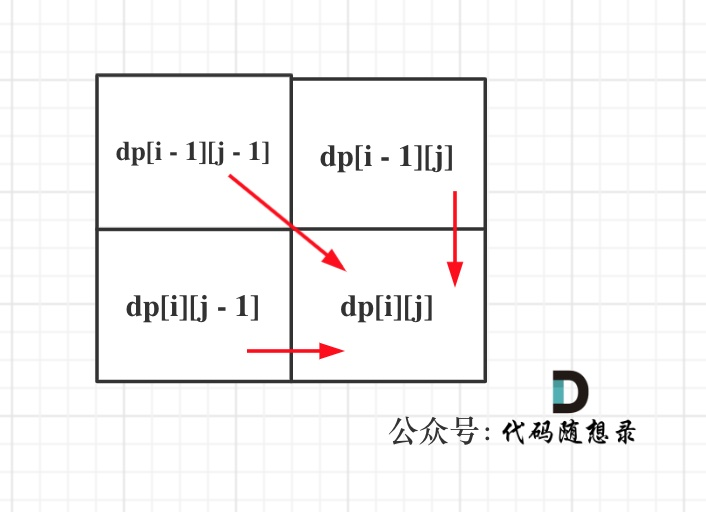
5.举例

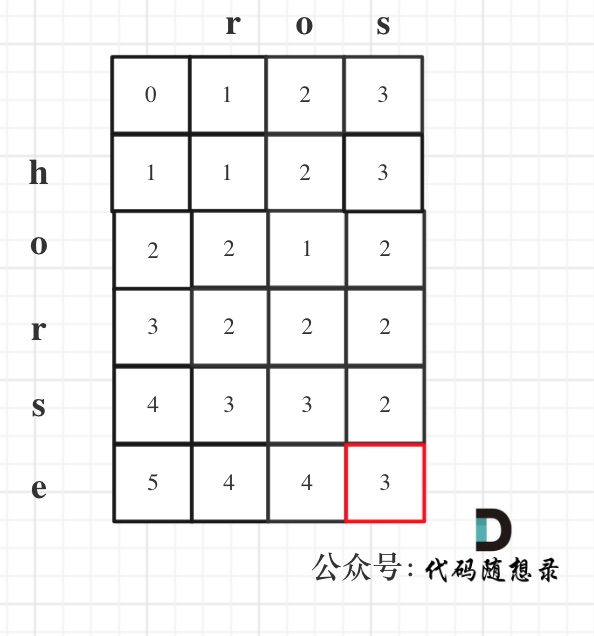
代码：

class Solution {
    public int minDistance(String word1, String word2) {
        int m = word1.length();
        int n = word2.length();
        int[][] dp = new int[m+1][n+1];
        for (int i = 1; i <= m; i++) dp[i][0] = i;
        for (int j = 1; j <= n; j++) dp[0][j] = j;
        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                if (word1.charAt(i - 1) == word2.charAt(j - 1)){
                    dp[i][j] = dp[i - 1][j - 1];
                } else {
                    dp[i][j] = Math.min(Math.min(dp[i - 1][j],dp[i][j - 1]),dp[i - 1][j - 1]) + 1;
                }
            }
        }
        return dp[m][n];
    }
}