机器学习算法之决策树
主要借鉴归纳: https://www.biaodianfu.com/decision-tree.html
01 什么是决策树
重要特征点
- 决策树依托策略决策, 建立起来的N叉树模型
- 决策树是一种预测模型
- 树中每个结点表示某种对象(多个特征的取值范围的集合),每个分叉路径依据某种标准进行分割,从根节点到叶子结点所经历的路径对应一个判定的测试序列
- 可以看做是在特征空间上的条件概率分布 ???
- 常见实践算法:基于启发式的贪心算法
优化决策树的方向
- 减少叶子结点
- 通过合并叶子结点(优化合并决策树),决策树的叶子结点越少,往往决策树的泛化能力越高
图示
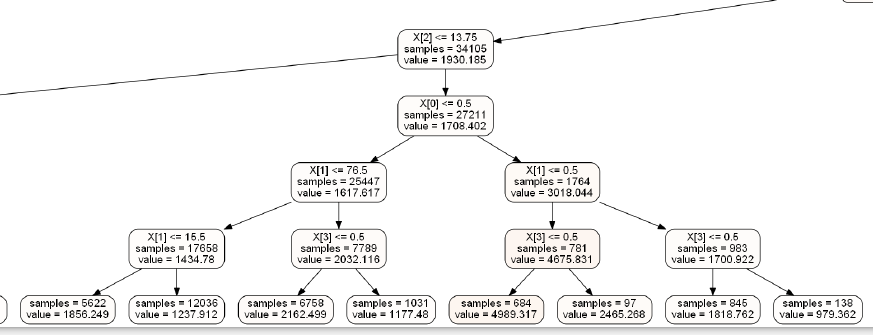
02 优缺点
优点
- 清晰,可以可视化,非常直观
- 可以用于分类和回归, 而且非常容易做多分类的分类 ???????????????????
- 能够处理数值型和连续的样本特征 ????????????
缺点 - 过拟合, 应对策略:进行剪枝可以缓解过拟合的负作用,如:限制树的高度、叶子结点的数量
- 不能简历全局最优的决策树,使用随机森林可以解决这个问题
基于ID3算法的决策分析
03 基于ID3算法的决策分析
- 简述: ID3算法是一种基于决策树的分类算法,基于信息熵的信息增益为衡量标准,从而实现对数据的归纳分类
- 算法策略: 根据信息增益(率), 运用自顶向下的贪心策略
- 主要优点: 建立的决策树的规模越小,查询的速度越快,即越小型的决策树越优于大的决策树
信息量是啥?
如
- 事件A:巴西队进入了2018世界杯决赛圈。(信息量小,概率大)
- 事件B:中国队进入了2018世界杯决赛圈。(信息量大,概率小)
可以简单定义: 信息量和事件发生的概率相关,事件发生的概率越低,传递的信息量越大

例如,
今天下雨的概率是0.5,则包含的信息量为 −log2(0.5)=1比特;
同理,下雨天飞机正常起飞的概率为0.25,则信息量为−log2(0.25)=2比特。
熵
定义: 用来度量信息的不确定程度。不确定程度越高,熵越高.
信息熵
信息熵(Entropy)是接受信息量的平均值,用于确定信息的不确定程度,是随机变量的均值。
信息熵越大,信息就越凌乱或传输的信息越多,熵本身的概念源于物理学中描述一个热力学系统的无序程度。信息熵的处理信息是一个让信息的熵减少的过程。
假设X是一个离散的随机变量,且它的取值范围为x1,x1,…,xn,每一种取到的概率分别是 p1,p1,…,pn,那么 X 的熵定义为:
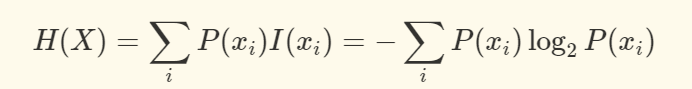
拓展 熵,条件熵,互信息,交叉熵 的理解总结 https://zhuanlan.zhihu.com/p/32401995
条件熵
若某个事件Xi下又分支有y1/y2,求条件熵时为了决定当前事件Xi是否值得继续向下贪心,步骤如下:
这里我们认为 Y 就是用某个维度进行切分,那么 y 就是切成的某个子集合于是 H(X|Y=y) 就是这个子集的熵。
因此可以认为就条件熵是每个子集合(y1、y2)的熵的一个加权平均/期望。
信息增益
当选择某个特征对数据集进行分类时,分类后的数据集信息熵会比分类前减少,减少的差值就是信息增益.
04 ID3算法流程
输入:数据集D,特征集A
输出:ID3决策树
流程:
- 对当前样本集合计算出所有属性信息的信息增益
- 先选择信息增益最大的属性作为测试属性,将测试属性相同的样本转化为同一个子样本
- 若子样本集的类别属性只含有单个属性,则分支为叶子节点,判断其属性值并标上相应的符号,然后返回调用处,否则对子样本递归调用本算法。