6/6
这场CFdiv2有六题,拖了很久终于补完了。。。。撒花~~撒花~~
题A Pineapple Incident
题意:告诉你 t, t + s, t + s + 1, t + 2s, t + 2s + 1……周期地发生什么,给你t,s,k,问你k可不可能是其中的某个数?
题解:简单题,先判断k是不是t,然后判断k-t和k-t-1是不是s的倍数即可。
题B Barnicle
题意:给你一个科学计数法表示的浮点数,展开它。
题解:注意0的情况和1.0e0的情况即可。
题C Lorenzo Von Matterhorn
题意:给你一颗二叉树,然后告诉你会有两种操作:
1.u v w表示u到v的路径的边增加w
2.u v询问路径权值为多少
题解:暴力!暴力!暴力!直接开个map暴力放进去,从u和v不断往前爬知道公共祖先。询问也一样。
题D Puzzles
题意:给你一棵树,然后让你模拟dfs,但是dfs的时候如果有多个结点,那么则随机选一个结点去访问,最后问你每个点访问时间的期望,假设访问一个结点用时1s。
题解:我们可以这样考虑,采用平均的策略,即(最好+最坏)/ 2;
最好:马上找到一个结点,用时1s
最坏:访问完剩余子树再来访问这个子树,那么就是其他子树的结点;
所以最后答案为:(假设当前树的sz为s1,要算的子树的sz为s2)
(s1 - s2 + 1) / 2;
题E PLEASE
题意:给你三个杯子,然后把要猜的东西放在中间,然后随意把左右的杯子拿来交换,做n次,然后最后猜的是中间,问你中的概率?这个n很大,他给你k个数,a1……ak,这k个数乘起来表示n。
题解:杯子的所有情况:
2 -> 13 -> 2312 -> 13122313……
2的出现次数为0、2、2、6……
最后可以推出这个序列为an = 2^n-1 - an-1,因为一共有2^n种可能,所以答案为:
bn = an / 2 ^ n,最后化简得:
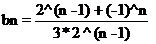
现在n = 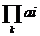 ,指数很大我们都用欧拉定理进行降幂,具体参考欧拉公式。因为这个mod是素数,所以我们可以把n % (mod - 2)来进行降幂。最后说一下这道题要求的输出方式:是把分子mod了之后分母mod了之后输出,但是这个分子分母来自于我们的推导公式,也就是分子 = an,分母 = 2 ^ n。
,指数很大我们都用欧拉定理进行降幂,具体参考欧拉公式。因为这个mod是素数,所以我们可以把n % (mod - 2)来进行降幂。最后说一下这道题要求的输出方式:是把分子mod了之后分母mod了之后输出,但是这个分子分母来自于我们的推导公式,也就是分子 = an,分母 = 2 ^ n。
题F Legen...
题意:给你n个串,每个串有自己的权值,构造一个长度为l的串使得这个串的权值最大,这个串的权值是n个串出现一次就会加上相应的权值。
题解:这道题要用到倍增floyd的思想。
先安利一篇论文里面解释了为什么能够这样做:
俞华程《矩阵乘法在信息学中的应用》
这里简单复述一下:
假设dp[i][j]为当前长度为i,末尾为j结点(Ac自动机构造的),然后转移方程为:
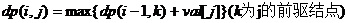
然后假设g[i][j]为i结点到j结点增加的权值,那么就可以类似地得到下面的矩阵转移方程:
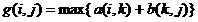
最后利用矩阵乘法加一下速即可。