HDU 3820 Golden Eggs

题意：有一个n*m的矩阵，里面可以放金蛋也可以放银蛋。分别给出在2个矩阵map1,map2表示在矩阵的每个格子里放金蛋的得分和放银蛋的得分。如果相邻的两个格子里都放了金蛋，则总得分要减去G，如果相邻的两个格子里都放了银蛋，则总得分要减去S。现要求你求出放蛋的最大得分。

跟HDU 3657比较像，但是这里更加复杂了，因为两种得分，一种金蛋，一种银蛋。所以我的理解是这里是两个二分图合起来的一个二分图，因为金蛋和银蛋存在一个匹配的关系，给矩阵染色后，黑格和白格也存在一个匹配的关系。因此，这样建图：假设行数i+列数j这和为偶数的格子为黑格，奇数的为白格，每个格子拆成两个点k,k'，分别表示放金蛋还是放银蛋，所以图中一共有2*n*m+2个点。

建图的方法大概是这样的：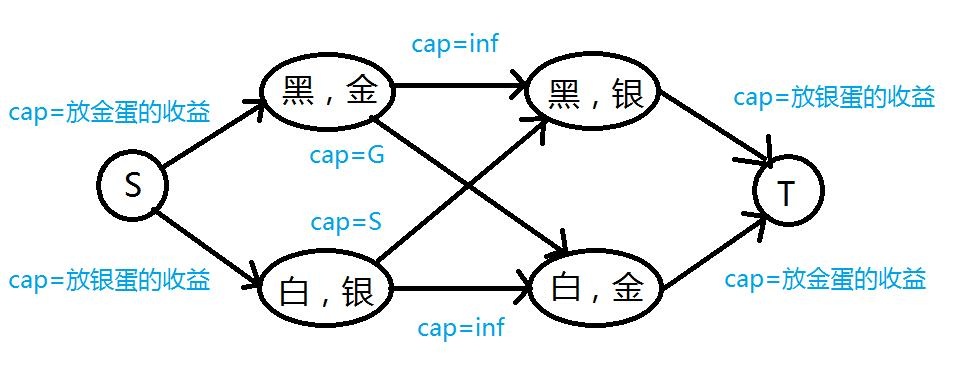

代码：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#define INF 1<<30
#define maxn 5010
#define maxm 100000
using namespace std;

int v[maxm],next[maxm],w[maxm];
int first[maxn],d[maxn],work[maxn],q[maxn];
int e,S,T;
int n,m,gold,silver;
int map1[55][55],map2[55][55];
void init(){
    e = 0;
    memset(first,-1,sizeof(first));
}

void add_edge(int a,int b,int c){
    //printf("add:%d to %d,cap = %d
",a,b,c);
    v[e] = b;next[e] = first[a];w[e] = c;first[a] = e++;
    v[e] = a;next[e] = first[b];w[e] = 0;first[b] = e++;
}

int bfs(){
    int rear = 0;
    memset(d,-1,sizeof(d));
    d[S] = 0;q[rear++] = S;
    for(int i = 0;i < rear;i++){
        for(int j = first[q[i]];j != -1;j = next[j])
            if(w[j] && d[v[j]] == -1){
                d[v[j]] = d[q[i]] + 1;
                q[rear++] = v[j];
                if(v[j] == T)   return 1;
            }
    }
    return 0;
}

int dfs(int cur,int a){
    if(cur == T)    return a;
    for(int &i = work[cur];i != -1;i = next[i]){
        if(w[i] && d[v[i]] == d[cur] + 1)
            if(int t = dfs(v[i],min(a,w[i]))){
                w[i] -= t;w[i^1] += t;
                return t;
            }
    }
    return 0;
}

int dinic(){
    int ans = 0;
    while(bfs()){
        memcpy(work,first,sizeof(first));
        while(int t = dfs(S,INF))   ans += t;
    }
    return ans;
}

int main()
{
    int nkase;
    scanf("%d",&nkase);
    for(int kase = 1;kase <= nkase;kase++){
        scanf("%d%d%d%d",&n,&m,&gold,&silver);
        S = 0,T = 2*n*m+1;
        init();
        int sum = 0,k = n*m;
        for(int i = 1;i <= n;i++){
            for(int j = 1;j <= m;j++)
                scanf("%d",&map1[i][j]),sum += map1[i][j];
        }
        for(int i = 1;i <= n;i++){
            for(int j = 1;j <= m;j++)
                scanf("%d",&map2[i][j]),sum += map2[i][j];
        }
        for(int i = 1;i <= n;i++){
            for(int j = 1;j <= m;j++){
                int pos = (i-1)*m+j;
                if((i+j)%2 == 1){
                    add_edge(S,pos,map1[i][j]);
                    add_edge(pos+k,T,map2[i][j]);
                    add_edge(pos,pos+k,INF);
                    if(i > 1)   add_edge(pos,pos-m,gold);
                    if(i < n)   add_edge(pos,pos+m,gold);
                    if(j > 1)   add_edge(pos,pos-1,gold);
                    if(j < m)   add_edge(pos,pos+1,gold);
                }else{
                    add_edge(S,pos+k,map2[i][j]);
                    add_edge(pos,T,map1[i][j]);
                    add_edge(pos+k,pos,INF);
                    if(i > 1)   add_edge(pos+k,pos+k-m,silver);
                    if(i < n)   add_edge(pos+k,pos+k+m,silver);
                    if(j > 1)   add_edge(pos+k,pos+k-1,silver);
                    if(j < m)   add_edge(pos+k,pos+k+1,silver);
                }
            }
        }
        printf("Case %d: %d
",kase,sum-dinic());
    }
    return 0;
}