L0正则化:L0是指向量中非0的个数。如果我们用L0范数来规则化一个参数矩阵W的话,就是希望W的大部分元素都是0。换句话说,让参数W是稀疏的。但不幸的是,L0范数的最优化问题是一个NP hard问题,而且理论证明,L1范数是L0范数的最优凸近似,因此通常使用L1范数来代替。
L1正则化:L1范数是指向向量中各个元素绝对值之和,也有个美称是“稀疏规则算子”(Lasso regularization)。
L2范数:也叫“岭回归”(Ridge Regression),也叫它“权值衰减weight decay”
但与L1范数不一样的是,它不会是每个元素为0,而只是接近于0。L2范数即是欧式距离。
正则化的作用
正则化的主要作用是防止过拟合,对模型添加正则化项可以限制模型的复杂度,使得模型在复杂度和性能达到平衡。
常用的正则化方法有L1正则化和L2正则化。L1正则化和L2正则化可以看作是损失函数的惩罚项。所谓“惩罚”就是对损失函数中的某些参数做一些限制。

L1和L2正则化的作用:
L1正则化可以产生稀疏权值矩阵,即产生一个稀疏模型,可以用于特征选择,一定程度上,L1也可以防止过拟合。
L2正则化可以防止模型过拟合(overfitting)
L2正则化可以直观理解为它对于大数值的权重向量进行严厉惩罚,倾向于更加分散的权重向量。由于输入和权重之间的乘法操作,这样就有一个优良的特性:使网络更倾向于使用所有输入特征,而不是严重依赖输入特征中某些小部分特征。L2惩罚倾向于更小更分散的权重向量,这就会鼓励分类器最终将所有维度上的特征都用起来,而不是强烈依赖其中少数几个维度,这样做可以提高模型的范化能力,降低过拟合的风险。
L1正则化有一个有趣的性质,他会让权重向量在最优化的过程中变得稀疏(即非常接近0)。也就是说,使用L1正则化的神经元最后使用的是它们最重要的输入数据的稀疏子集,同时对于噪音输入则几乎是不变的了,相较于L1正则化,L2正则化中的权重向量大多是分散的小数字。
在实践中,如果不是特别关注某些明确的特征选择,一般说来L2正则化都会比L1正则化效果好。
L1和L2正则化的原理


上面的图,左面是L2约束下解空间的图像,右面是L1约束下解空间的图像。
蓝色的圆圈表示损失函数的等值线。同一个圆上的损失函数值相等的,圆的半径越大表示损失值越大,由外到内,损失函数值越来越小,中间最小。
如果没有L1和L2正则化约束的化,w1和w2是可以任意取值的,损失函数可以优化到中心的最小值的,此时中心对应的w1和w2的取值就是模型最终求得的参数。
但是添加了L1和L2正则化约束就把解空间约束在了黄色的平面内。黄色图像的边缘与损失函数等值线的交点,便是满足约束条件的损失函数最小化的模型的参数的解。由于L正则化约束的解空间是一个菱形,所以等值线与菱形端点相交的概率比与线的之间相交的概率要大很多,端点在坐标轴上,一些参数的取值便为0.L2正则化的解空间是圆形,所以等值线与圆的任何部分相交的概率都是一样的,所以也就不会产生稀疏的参数。
但是L2为什么倾向于产生分散的参数呢?那是因为求解模型的时候要求,在约束条件满足的情况下最小化损失函数,w的平方和也应该尽可能的小。
举个例子:
设输入向量x=[1, 1, 1, 1],两个权重向量w_1=[1, 0, 0, 0],w_2=[0.25, 0.25, 0.25, 0.25]。那么w1T*x=1,w2T*x=1,两个权重向量都得到同样的内积,但是w1的L2惩罚是1.0,而w2的L2惩罚是0.25.因此,根据L2惩罚来看,w2更好,因为它的正则化损失更小。从直观上来看,这是因为w2的权重值更小且更分散。所以L2正则化倾向于是特征分散,更小。
3、正则化的参数λ
我们一般会为正则化项添加一个超参数λ或a,用来平衡经验风险和结构风险(正则项表示结构风险)。
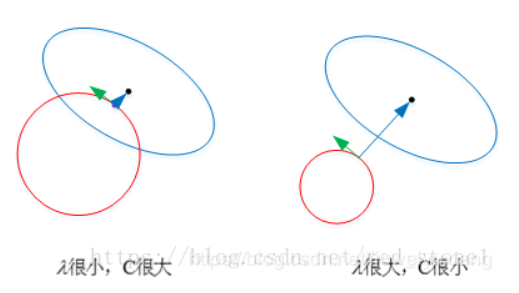
以L2为例,若λ很小,就是说我们考虑经验风险更多一些,对于结构风险没有那么重视,约束条件更为宽松,这时圆形区域很大,能够让w更接近中心最优解的位置。若λ近似为0,相当于圆形区域覆盖了最优解位置,这时候,正则化失效,容易造成过拟合。
相反,若λ很大,约束条件更为严格,对应上文中的C值就很小,这时候,圆形区域很小,w离中心最优解的位置较远。w被限制在一个很小的区域内变化,w普遍较小且接近0,起到了正则化的效果。但是,λ过大容易造成欠拟合。欠拟合和过拟合是两种对立的状态。
4总结
1、添加正则化相当于参数的解空间添加了约束,限制了模型的复杂度
2、L1正则化的形式是添加参数的绝对值之和作为结构风险项,L2正则化的形式添加参数的平方和作为结构风险项
3、L1正则化鼓励产生稀疏的权重,即使得一部分权重为0,用于特征选择;L2鼓励产生小而分散的权重,鼓励让模型做决策的时候考虑更多的特征,而不是仅仅依赖某几个特征,可以增强模型的泛化能力,防止过拟合。
4、正则化参数λ越大,约束越严格,太大容易产生欠拟合。正则化参数λ越小,约束宽松,太小起不到约束作用,容易产生过拟合。
5、如果不是为了进行特征选择,一般使用L2正则化模型效果更好。
********除此之外,正则化的方法还有很多,如下*************
1、参数范数惩罚,如上介绍
2、数据集增强
让机器学习模型范化得更好的最好办法是使用更多的数据进行训练。当然,在实践中,我们拥有的数据量是很有限的。解决这个问题的一种方法是创建假数据并添加到训练集中。我们必须要小心,不能使用改变类别的转换。在神经网络的输入层注入噪声,也可以被看作是数据增强的一种方式。
3、噪声鲁棒性
对于某些模型而言,向输入添加方差极小的噪声等价于对权值施加范数惩罚。在一般情况下,噪声注入远比简单地收缩参数强大,特别是噪声被添加到隐藏单元时会更加强大。主要是将正则化的噪声添加到权重,第二种是向输出目标中注入噪声。
4、多任务学习:是通过合并几个任务中的样例来提高范化的一种方式。当模型的一部分在任务之间共享时,模型的这一部分更多地被约束为良好的值,往往能更好地范化。
5、提前终止:当训练有足够的表示能力甚至会过拟合的大模型时,我们经常观察到,训练误差会随着时间的退役逐渐降低,但验证集的误差会再次上升。这意味着如果我们返回使验证集误差最低的参数设置,就可以获得更好的模型。
6、参数绑定和参数共享:目前为止,最流行和广泛使用的参数共享出现在应用于计算机视觉的卷积神经网络(CNN)中。
7、稀疏表示:权重衰减直接惩罚模型参数,另一种策略是惩罚神经网络中的激活单元,稀疏化激活单元。这种策略间接地对模型参数施加了复杂惩罚。含有隐藏层单元的模型在本质上都能变得稀疏。
8、Bagging和其他集成方法:Bagging(bootstrap aggregating)是通过结合几个模型降低范化误差的技术。主要想法是分别训练几个不同的模型,然后让所有模型表决测试样例的输出。这是机器学习中常规策略的一个例子,被称为模型平均(model averaging)。
9、dropout
10、对抗训练:我们可以通过对抗训练减少原有独立同分布的测试集的错误率---在对抗扰动的训练集样本上训练网络。
11、切面距离、正切传播和流行正切分类器。
参考:深度学习中的正则化简介
https://blog.csdn.net/fengbingchun/article/details/79910284