灰度聚类
接着我们就对图像的色彩进行聚类。聚类的有两个事实依据：
1.灰度分辨率 肉眼的灰度分辨率大概为40，因此对于像素值254和255，在我们肉眼看来都 只是白色；
2.设计原则 根据我们一般的审美原则，在考虑海报设计、服装搭配等搭配的时候，一般要 求在服装、海报等颜色搭配不超过三种颜色。
更通俗地说，虽然灰度图片色阶范围是[0, 255]，但我们能感觉到的整体的色调一般不多，因此，可以将相近的色阶归为一类，从而减少颜色分布，有效地降低噪音。
事实上，聚类是根据图像的特点自适应地进行多值化的过程，避免了传统的简单二值化所带来 的信息损失。由于我们需要自动地确定聚类数目，因此传统的KMeans等聚类方法被我们抛弃 了，而且经过我们测试，诸如MeanShift等可行的聚类方法又存在速度较慢等缺陷。因此，我们 自行设计了聚类方法，使用的是“核概率密度估计”的思路，通过求颜色密度极值的方式来聚类。
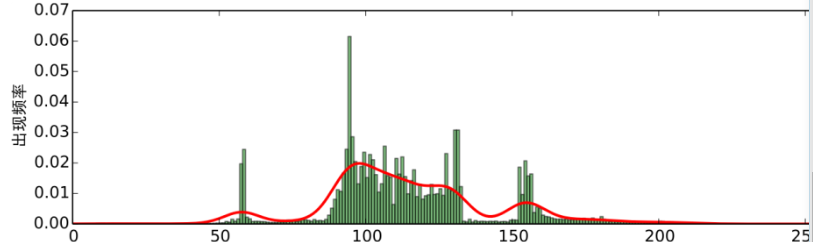
核密度估计 经过预处理的图像，我们可以对每个色阶的出现次数进行统计，根据色戒，得到如图5的频率分布直方图：
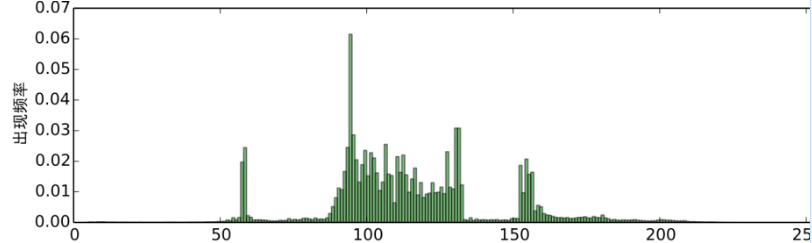
可以看到，色阶的分布形成了几个比较突出的峰，换言之，存在一定的聚类趋势。 然而，直方 图的统计结果是不连续的，一个平滑的结果更便于我们分析研究，结果也更有说服力。 将统计 结果平滑化的方法，就是核密度估计(kernel density estimation)。
核密度估计方法是一种非参数估计方法，由Rosenblatt和Parzen提出，在统计学理论和应用领 域均受到高度的重视[2]。 当然，也可以简单地将它看成一种函数平滑方式。 我们根据大量的数据 来估计某个值出现的概率(密度)时，事实上做的是如下估算：
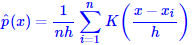
其中K(x)称为核函数。 当 取为1，且K(x)取
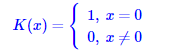
时，就是我们上述的直方图估计。 K(x)这一项的含义很简单，它就是告诉我们在范围h内的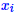
都算入到x中去，至于怎么算，由
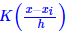给出。可见，h的选择对结果的影响很大，h我们称之为带宽(bandwidth)，它主要影响结果的平滑性。 如果K(x)是离散的，得到的结果还是离散的，但如果K(x)是光滑的，得到的结果也是比较光滑的。一个常用的光滑函数核是高斯核：
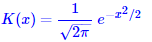
所得到的估计也叫高斯核密度估计。 在这里，我们使用scott规则自适应地选取 ，但需要手动指定一个平滑因子，在本文中，我们选取为0。2。对于示例图片，我们得到如图6的红色曲线的结果。
极大极小值分割
从图6中我们进一步可以看出，图像确实存在着聚类趋势。 这表现为它有几个明显的极大值和极 小值点，这里的极大值点位于x = 10, 57, 97, 123, 154，极小值点位于25, 71, 121, 142。
因此，一个很自然的聚类方法是：有多少个极大值点，就聚为多少类，并且以极小值点作为类 别之间的边界。 也就是说，对于图3，可以将图像分层5层，逐层处理。 分层之后，每一层的形状 如下图，其中白色是1，黑色是0。
通过聚类将图像分为5个图层
可见，由于“对比度”和“渐变性”假设，通过聚类确实可以将文字图层通过核密度估计的聚类方 法分离开来。 而且，通过聚类分层的思路，无需对文字颜色作任何假定，即便是文字颜色跟背 景颜色一致时，也可以获得有效检测。
逐层识别
当图像有效地进行分层后，我们就可以根据前面的假设，进一步设计相应的模型，通过逐层处 理的方式找出图像中的文字区域。