原文:https://herbertmj.wikispaces.com/stacking%E7%AE%97%E6%B3%95
stacked 产生方法是一种截然不同的组合多个模型的方法,它讲的是组合学习器的概念,但是使用的相对于bagging和boosting较少,它不像bagging和boosting,而是组合不同的模型,具体的过程如下:
1.划分训练数据集为两个不相交的集合。
2. 在第一个集合上训练多个学习器。
3. 在第二个集合上测试这几个学习器
4. 把第三步得到的预测结果作为输入,把正确的回应作为输出,训练一个高层学习器,
这里需要注意的是1-3步的效果与cross-validation,我们不是用赢家通吃,而是使用非线性组合学习器的方法
下面是weka的stacking方法的buildClassifier方法:
http://www.datakit.cn/blog/2014/11/02/Ensemble_learning.html
在机器学习和统计学习中, Ensemble Learning(集成学习)是一种将多种学习算法组合在一起以取得更好表现的一种方法。与 Statistical Ensemble(统计总体,通常是无限的)不同,机器学习下的Ensemble 主要是指有限的模型相互组合,而且可以有很多不同的结构。相关的概念有多模型系统、Committee Learning、Modular systems、多分类器系统等等。这些概念相互之间相互联系,又有区别,而对这些概念的界定,业界目前还没有达成共识。
本文主要参考wikipedia, wikipedia中参考文章不再罗列!部分参考scholarpedia。本文对Ensemble方法仅作概述!
目录
- 1.Overview
- 2.Ensemble theory
- 3.Common types of ensembles
- 3.4 Bayesian model averaging
- 4. Ensemble combination rules
1.Overview
机器学习中,监督式学习算法(Supervised learning)可以描述为:对于一个具体问题,从一堆”假设”(hypothesis space,”假设”空间)中搜索一个具有较好且相对稳定的预测效果的模型。有些时候,即使”假设”空间中包含了一些很好的”假设”(hypothesis) ,我们也很难从中找到一个较好的。Ensemble 的方法就是组合多个”假设”以期望得到一个较优的”假设”。换句话说,Ensemble的方法就是组合许多弱模型(weak learners,预测效果一般的模型) 以得到一个强模型(strong learner,预测效果好的模型)。Ensemble中组合的模型可以是同一类的模型,也可以是不同类型的模型。
Ensemble方法对于大量数据和不充分数据都有很好的效果。因为一些简单模型数据量太大而很难训练,或者只能学习到一部分,而Ensemble方法可以有策略的将数据集划分成一些小数据集,分别进行训练,之后根据一些策略进行组合。相反,如果数据量很少,可以使用bootstrap进行抽样,得到多个数据集,分别进行训练后再组合(Efron 1979)。
使用Ensemble的方法在评估测试的时候,相比于单一模型,需要更多的计算。因此,有时候也认为Ensemble是用更多的计算来弥补弱模型。同时,这也导致模型中的每个参数所包含的信息量比单一模型少很多,导致太多的冗余!
注:本文直接使用Ensemble这个词,而不使用翻译,如“组合”等等
2.Ensemble theory
Ensemble方法是监督式学习的一种,训练完成之后就可以看成是单独的一个”假设”(或模型),只是该”假设”不一定是在原”假设”空间里的。因此,Ensemble方法具有更多的灵活性。理论上来说,Ensemble方法也比单一模型更容易过拟合。但是,实际中有一些方法(尤其是Bagging)也倾向于避免过拟合。
经验上来说,如果待组合的各个模型之间差异性(diversity )比较显著,那么Ensemble之后通常会有一个较好的结果,因此也有很多Ensemble的方法致力于提高待组合模型间的差异性。尽管不直观,但是越随机的算法(比如随机决策树)比有意设计的算法(比如熵减少决策树)更容易产生强分类器。然而,实际发现使用多个强学习算法比那些为了促进多样性而做的模型更加有效。
下图是使用训练集合中不同的子集进行训练(以获得适当的差异性,类似于合理抽样),得到不同的误差,之后适当的组合在一起来减少误差。
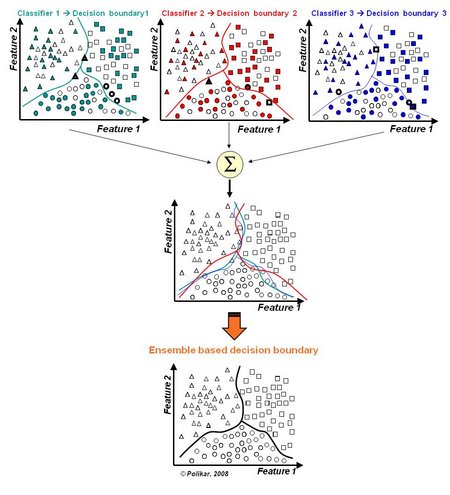
3.Common types of ensembles
3.1 Bayes optimal classifier
贝叶斯最优分类器(Bayes Optimal Classifier)是分类技术的一种,他是”假设”空间里所有”假设”的一个Ensemble。通常来说,没有别的Ensemble会比它有更好的表现!因此,可以认为他是最优的Ensemble(见Tom M. Mitchell, Machine Learning, 1997, pp. 175)。如果”假设”是对的话,那每一个”假设”对从系统中产生训练数据的似然性都有一个投票比例。为了促使训练数据集大小是有限的,我们需要对每个”假设”的投票乘上一个先验概率。因此,完整的Bayes Optimal Classifier如下:
y=argmaxcj∈C∑hi∈HP(cj|hi)P(T|hi)P(hi)
这里y是预测的类,C是所有可能的类别,H是”假设”空间,P是概率分布, T是训练数据。作为一个Ensemble,Bayes Optimal Classifier代表了一个”假设”,但是不一定在H中,而是在Ensemble空间(是原”假设”空间里的”假设”的所有可能的Ensemble)里的最优”假设”。然而,在实际中的很多例子中(即使很简单的例子),Bayes Optimal Classifier并不能很好的实现。实际中不能很好的实现Bayes Optimal Classifier的理由主要有以下几个:
- 1) 绝大多数”假设”空间都非常大而无法遍历(无法 argmax了);
- 2) 很多”假设”给出的结果就是一个类别,而不是概率(模型需要P(cj|hi));
- 3) 计算一个训练数据的无偏估计P(T|hi)是非常难的;
- 4) 估计各个”假设”的先验分布P(hi)基本是不可行的;
3.2 Bootstrap aggregating
Bootstrap aggregating通常又简称为Bagging(装袋法),它是让各个模型都平等投票来决定最终结果。为了提高模型的方差(variance, 差异性),bagging在训练待组合的各个模型的时候是从训练集合中随机的抽取数据。比如随机森林(random forest)就是多个随机决策树平均组合起来以达到较优分类准确率的模型。 但是,bagging的一个有趣应用是非监督式学习中,图像处理中使用不同的核函数进行bagging,可以阅读论文Image denoising with a multi-phase kernel principal component approach and an ensemble version 和 Preimages for Variation Patterns from Kernel PCA and Bagging。

3.3 Boosting
Boosting(提升法)是通过不断的建立新模型而新模型更强调上一个模型中被错误分类的样本,再将这些模型组合起来的方法。在一些例子中,boosting要比bagging有更好的准确率,但是也更容易过拟合。目前,boosting中最常用的方法是adaboost.

3.4 Bayesian model averaging
Bayesian model averaging (BMA, 贝叶斯模型平均)是一个寻求近似于Bayes Optimal Classifier 的方法,他通过从”假设”空间里抽样一些”假设”,再使用贝叶斯法则合并起来。 与Bayes Optimal Classifier不同,BMA是可以实际实现的。可以使用 Monte Carlo sampling 来采样”假设”。 比如, 使用Gibbs 抽样(Gibbs sampling)来得到一堆”假设”P(T|H)。事实证明在一定情况下,当这些生成的”假设”按照贝叶斯法则合并起来后,期望误差不大于2倍的Bayes Optimal Classifier 的期望误差。先不管理论上的证明,事实表明这种方法比简单的Ensemble方法(如bagging)更容易过拟合、且表现更差。然而,这些结论可能是错误理解了Bayesian model averaging和model combination的目的(前者是为了近似Bayes Optimal Classifier,而后者是为了提高模型准确率)。
伪代码如下:
function train_bayesian_model_averaging(T)
z = -infinity
For each model, m, in the ensemble:
Train m, typically using a random subset of the training data, T.
Let prior[m] be the prior probability that m is the generating hypothesis.
Typically, uniform priors are used, so prior[m] = 1.
Let x be the predictive accuracy (from 0 to 1) of m for predicting the labels in T.
Use x to estimate log_likelihood[m]. Often, this is computed as
log_likelihood[m] = |T| * (x * log(x) + (1 - x) * log(1 - x)),
where |T| is the number of training patterns in T.
z = max(z, log_likelihood[m])
For each model, m, in the ensemble:
weight[m] = prior[m] * exp(log_likelihood[m] - z)
Normalize all the model weights to sum to 1.3.5 Bayesian model combination
Bayesian model combination(BMC) 是 BMA 的一个校正算法。它不是独立的生成Ensemble中的一个个模型,而是从可能的Ensemble Space中生成(模型的权重是由同一参数的Dirichlet分布生成)。这个修正克服了BMA算法给单个模型所有权重的倾向。尽管BMC比BMA有更多的计算量,但是它的结果也非常的好!有很多例子证明了BMC比BMA和bagging的效果更好。
对于BMA而言,使用贝叶斯法来计算模型权重就必须要计算给定各个模型时生成数据的概率P(T|hi)。通常情况下,Ensemble中的模型都不是严格服从训练数据的生成分布来生成数据,所以这一项一般都非常接近于0。如果Ensemble足够大到可以抽样整个”假设”空间,那么理论上结果是比较好。但是,Ensemble空间有限,不可行。因此,训练数据中的每个模式会导致Ensemble中与训练数据分布最接近的模型的权重增大。举一个例子来说,比如”假设”空间有5个假设,BMA与BMC可以简单的如下图所示:

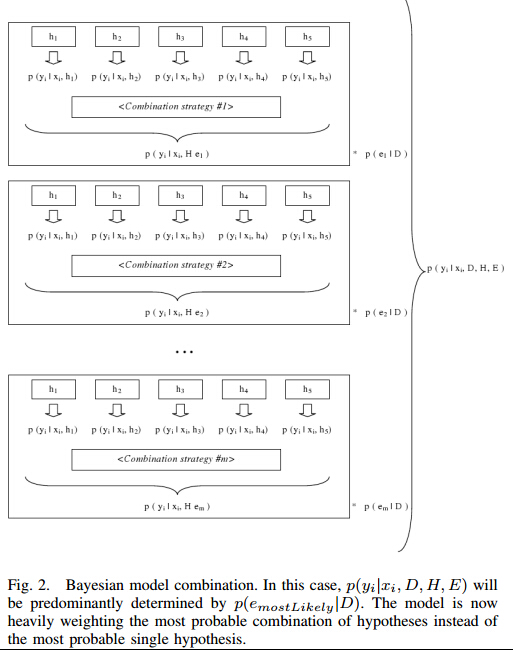
BMA是选择一个与生成数据的分布最接近的模型,而BMC是选择一个与生成数据的分布最接近的模型组合方式。BMA可以看成是从一堆模型中使用交叉验证来选择一个最优模型。而BMC可以认为是从一堆随机模型组合中选择一个最好的组合(Ensemble)。
伪代码如下:更多信息可以阅读Turning Bayesian Model Averaging Into Bayesian Model Combination
function train_bayesian_model_combination(T)
For each model, m, in the ensemble:
weight[m] = 0
sum_weight = 0
z = -infinity
Let n be some number of weightings to sample.
(100 might be a reasonable value. Smaller is faster.
Bigger leads to more precise results.)
for i from 0 to n - 1:
For each model, m, in the ensemble: // draw from a uniform Dirichlet distribution
v[m] = -log(random_uniform(0,1))
Normalize v to sum to 1
Let x be the predictive accuracy (from 0 to 1) of the entire ensemble, weighted
according to v, for predicting the labels in T.
Use x to estimate log_likelihood[i]. Often, this is computed as
log_likelihood[i] = |T| * (x * log(x) + (1 - x) * log(1 - x)),
where |T| is the number of training patterns in T.
If log_likelihood[i] > z: // z is used to maintain numerical stability
For each model, m, in the ensemble:
weight[m] = weight[m] * exp(z - log_likelihood[i])
z = log_likelihood[i]
w =