哈密尔顿回路总结

一、引子

1959 年 William Rowan Hamilton 发明了一个小玩具，这个玩具是一个木刻的正十二面体，每面系正五角形，三面交于一角，共 20 个角，没每个角上标有世界上一个重要城市。他提出一个问题：要求沿着正十二面体的边寻找一条路，通过 20 个城市，而每个城市只通过一次，最后返回原地。Hamilton 将此问题称为周游世界问题，并且坐了肯定的回答。

上面提到的问题就是经典的 Hamilton 回路问题。

当然，还有另一个著名的回路问题——欧拉回路问题，不同于 Hamilton 回路问题，欧拉问题已经得到了圆满解决

二、一些定义

设无向图 G=(V, E)，其中 V 是点集，E 是边集， n=|V| 表示图中点的数量，m=|E| 表示图中边的数量

Hamilton 通路：经过图 G 中每个节点一次且仅一次的通路称为 Hamilton 通路

　　特点：包含图 G 中所有顶点，通路上各顶点不重复

Hamilton 回路：经过图 G 中每个节点一次且仅一次的回路称为 Hamilton 回路

　　特点：包含图 G 中所有顶点，回路中，除了起点和终点相同之外，回路上各点不重复

Hamilton 图：存在 Hamilton 回路的图称为 Hamilton 图

Hamilton 通路问题转化为 Hamilton 回路问题：

　　一个可行的做法是枚举通路的起点和终点，添加一条边，转化为对应 Hamilton 回路问题

三、Hamilton 图的判定

众所周知，现在没有判断图中是否存在 Hamilton 通路、Hamilton 回路的简单判定定理，我们只能对节点较少的图凭经验去判定，下面给出的是一些必要条件和充分条件以及相应的简单证明

PS：这些证明当然不是我写的啦，都是抄的书上的，不过我都理解了

1、必要条件：

定理1：设无向图 G=(V, E) 是 Hamilton 图，V1 是 V 的任意非空子集，则：p(G-V1)≤|V1|（其中：p(G-V1) 表示从 G 中删除 V1 后得到的图的联通分支的数量）

证明：

考虑 G 的一条 Hamilton 回路 C，显然 C 是 G 的生成子图，从而 C-V1 也是 G-V1 的生成子图，且有 p(G-V1)≤p(C-V1)，因此只需要证明 p(C-V1)≤|V1|即可。

下面分两种情况讨论：

　　（1）、V1 中节点在 C 中均相邻，删除 C 上 V1 中各点及关联的边后，C-V1 仍是联通的，但已非回路，因此 p(C-V1)=1≤|V1|

　　（2）、V1 中节点在 C 中存在 r(2≤r≤|V1|) 个互不相邻，删除 C 上 V1 中各点及关联的边后，将 C 分为互不相连的 r 段，即 p(C-V1)=r≤|V1|

一般情况下，V1 中的点在 C 中既有相邻的也有不相邻的，因此总有 p(C-V1)≤|V1|

又因为 C 是 G 的生成子图，从而 C-V1 也是 G-V1 的生成子图，故有：p(G-V1)≤p(C-V1)≤|V1|

推论1.1：设无向图 G=(V, E) 中存在 Hamilton 通路，则对 V 的任意非空子集 V1，都有 p(G-V1)≤|V1|+1

上面的定理和推论在用来判断一个图是否存在 Hamilton 回路（通路）时非常有用

2、充分条件：

定理2：设 G=(V, E) 是具有 n 个节点的简单无向图（|V|=n），如果对于任意的两个不相邻的节点 u, v∈V，均有 deg(u)+deg(v)≥n-1，则 G 中一定存在 Hamilton 通路

证明：

首先证明满足上述条件的图是一个联通图，然后用“延长通路法”找出一条 Hamilton 通路

（1）、反证法证明满足上述条件的图是一个连通图：

假设 G 有两个或者更多联通分支。设一个联通分支有 n1 个节点，另一个联通分支有 n2 个节点。这两个联通分支中分别有节点 v₁ 和节点 v₂。显然：deg(v₁)≤n1-1，deg(v₂)≤n2-1。从而：deg(v₁)+deg(v₂)≤n1+n2-2≤n-2，与已知条件"对于任意的两个不相邻的节点 u, v∈V，均有 deg(u)+deg(v)≥n-1"矛盾，故 G 是联通的

（2）、证明 G 中存在 Hamilton 通路

设 p=v₁v₂...v_k 为 G 中用“延长通路法”得到的“极大基本通路”，即 p 中的始点 v₁ 和终点 v_k 不与 p 外的节点相邻，显然 k≤n

　　（Ⅰ）、若 k=n，则 p 为 G 中经过所有节点的通路，即为 Hamilton 通路

　　（Ⅱ）、若 k<n，说明 G 中还存在 p 外的节点，但此时可以证明存在仅经过 p 上所有节点的基本回路，证明如下：

　　　　（a）、若在 p 上 v₁ 与 v_k 相邻，则 v₁v₂...v_kv₁ 为仅经过 p 上所有节点的基本回路

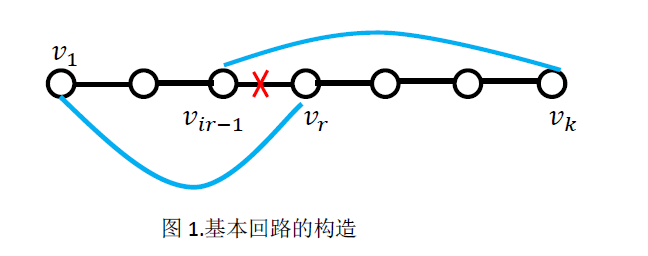
　　　　（b）、若在 p 上 v₁ 不与 v_k 相邻，假设 v₁ 在 p 上与 v_i=v₂,v_i2,v_i3，...，v_ij 相邻（j 必然大于等于 2，否则 deg(v₁)+deg(v_k)≤1+k-2<n-1），此时，v_k 必定与 v_i2,v_i3，...，v_ij 中相邻的节点 v_i2-1,v_i3-1，...，v_ij-1 至少一个相邻（否则 deg(v₁)+deg(v_k)≤j+k-2-(j-1)=k-1<n-1）。设 v_k 与 v_ir-1(2≤r≤j) 相邻，如下图所示：在 p 中添加边 (v₁, v_ir)，(v_k, v_ir-1)，删除边 (v_ir-1, v_ir) 得到基本回路：C=v₁v₂...v_ir-1v_kv_k-1...v_irv₁

　　　　  　 

　　（Ⅲ）、证明存在比 p 更长的通路

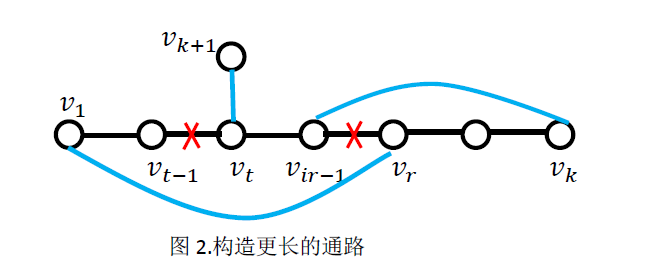
　　  　　因为 k<n，所以 V 中还有一些节点不在 C 中，由 G 的联通性可知，存在 C 外的节点与 C 上的节点相邻，不妨设 v_k+1∈V-V(C)，且与 C 上的节点 v_t 相邻，在 C 中删除边 (v_t-1, v_t)，添加边 (v_t, v_k+1) 从而得到通路 p'=v_t-1...v₁v_ir...v_kv_ir-1...v_tv_k+1，如下图所示，显然，p‘ 比 p 长 1，且 p’ 上有 k+1 个不同的节点。

　　　　　　

对 p‘ 重复 （Ⅰ）~（Ⅲ），得到 G 中 Hamilton 通路或比 p’ 更长的基本通路，由于 G 中节点数目有限，故在有限步内一定能得到 G 中一条 Hamilton 通路

推论2.1：设 G=(V, E) 是具有 n 个节点的简单无向图，如果对于任意两个不相邻的节点 u, v∈V，均有 deg(u)+deg(v)≥n，则 G 中一定存在 Hamilton 回路

需要指出的是，推论2.1就是著名的 Ore 定理

推论2.2：设 G=(V, E) 是具有 n 个节点的简单无向图，n≥3，如果对于任意的 u∈V，均有 deg(v)≥n/2，则 G 是 Hamilton 图

四、刷题练手

额，暂时只写了一道题目，还是非常裸的求 Hamilton 回路的题目 : SGU 122 The book

题目大意：给一个含有 n(2≤n≤1000) 个点的无向图，图中每个顶点至少有 (n+1)/2 个相邻点，让求一条 Hamilton 回路

注意到 "每个顶点至少有 (n+1)/2 个相邻点" 这句话，满足 Ore 定理，直接构造解即可，构造的方法就是在证明定理 2 时使用的方法

#include <cstring>
#include <cstdio>
#include <iostream>
#include <list>

using namespace std;

struct Hamilton_Circuit {
    static const int N=1006;

    bool G[N][N], vs[N];
    int n, next[N], head, tail;

    void init(int _n) {
        n=_n;
        memset(G, 0, sizeof G);
    }

    void DFS_Head(int u) {
        vs[u]=1;
        for(int i=0; i<n; i++) if(G[i][u] && !vs[i]) {
            next[i]=u;
            DFS_Head(i);
            return;
        }
        head=u;
    }

    void DFS_Tail(int u) {
        vs[u]=1;
        for(int i=0; i<n; i++) if(G[u][i] && !vs[i]) {
            next[u]=i;
            DFS_Tail(i);
            return;
        }
        tail=u;
    }

    void Reverse(int u) {
        for(int i=next[u], temp, last=-1; i!=-1; i=temp) {
            temp=next[i];
            next[i]=last;
            last=i;
        }
        int temp=tail;
        tail=next[u];
        next[u]=temp;
    }

    int Find(int u) {
        for(int i=head; i!=-1; i=next[i]) {
            if(G[u][next[i]]) return i;
        }
        return -1;
    }

    bool Extend(int u) {
        if(G[u][head]) {
            next[u]=head;
            return 1;
        }
        int pre=Find(u);
        if(pre==-1) return 0;
        next[u]=next[pre];
        next[tail]=head;
        next[tail=pre]=-1;
        return 1;
    }

    void Solve() {
        memset(next, -1, sizeof next);
        memset(vs, 0, sizeof vs);
        DFS_Head(0), DFS_Tail(0);
        int Len=1;
        for(int i=head; i!=tail; i=next[i], Len++);
        for(int i; 1; ) {
            if(!G[tail][head]) {
                for(i=next[head]; !(G[i][tail] && G[next[i]][head]); i=next[i]);
                Reverse(i);
            }
            if(Len==n) break;
            for(i=0; i<n; i++) if(!vs[i] && Extend(i)) {
                head=i, vs[i]=1, Len++;
                break;
            }
        }
    }

    void PRINT() {
        for(int i=head; head!=0; i=next[i]) {
            next[tail]=head;
            tail=head;
            head=next[head];
            next[tail]=-1;
        }
        for(int i=head; i!=-1; i=next[i]) {
            printf("%d", i+1);
            if(next[i]==-1) printf(" 1
");
            else printf(" ");
        }
    }
};

Hamilton_Circuit fuck;
int n;

int main() {
    scanf("%d", &n);
    fuck.init(n);
    for(int i=0; i<n; i++) {
        for(int x; ; ) {
            scanf("%d", &x);
            fuck.G[i][x-1]=1;
            x=getchar();
            if(x=='
' || x=='
' || x==EOF) break;
        }
    }
    fuck.Solve();
    fuck.PRINT();
    return 0;
}