题解 【P4315】 月下“毛景树”

看原题戳这儿

如题，肯定是树链剖分的题。

零、写在前面

建议先A掉这道模板题（不会的先看这个）

前置知识：链式前向星，树，dfs序，LCA，树形dp，线段树，树链剖分(······)

一定要先完全学懂，否则不保证这篇题解能完全看懂！！！

一、审题

先简化题目：

已知一棵包含 (N(0 le N le 100000)) 个结点的树（连通且无环），每条边上包含一个数值，需要支持以下操作：

• (Change k w)：将第(k)条边上数值改变为(w)。

• (Covr u v w)：将节点(u)与节点(v)之间的最短路径上数值都改变为(w)个。

• (Add u v w)：将节点(u)与节点(v)之间的最短路径上数值都增加(w)。

• (Max u v)：询问节点(u)与节点(v)之间的最短路径上的数值之和最大是多少。

瞄一眼数据，(N)最大是({10}^5)，肯定要用(O(nlogn))的算法，树剖和线段树刚好合适。

二、难点

这道题虽然说已经确定下来要用树链剖分来做了，但是树链剖分和线段树不都是求点吗？怎么可以用来求边呢？这就是这道题目的毒瘤之处。

那应该怎么做呢？

答：边权换点权！！！

实现

如下图所示，把每边权值赋给其下端的点（根节点为0）

然后就是模板的问题了

但有几个细节，本题又加又覆，需要两个懒标记，记得处理他们的关系

还有一件事，当查询时转化为一条重链时，如图：

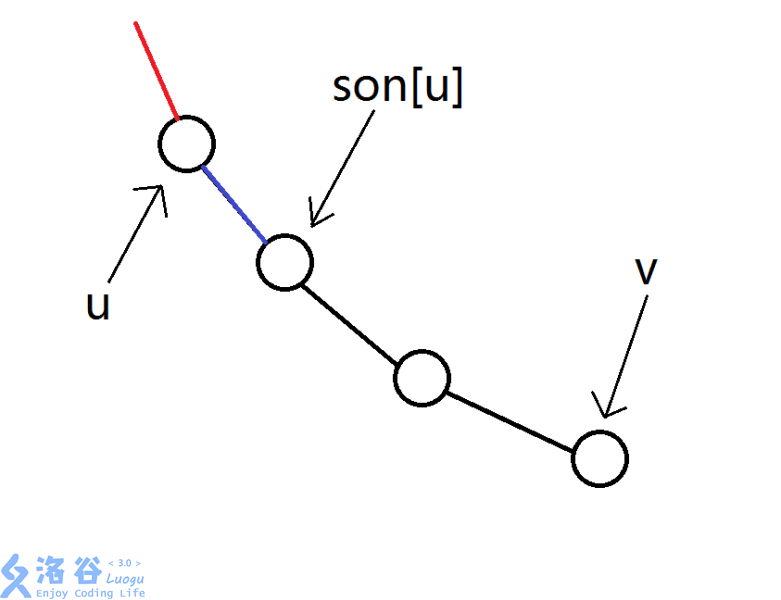
此时我们要求(u,v)两点间的权值最大值，但是(u)节点存的是红边的值，这不是我们要找的答案

而(sun_u)存的是蓝边，这正是我们的目标

所以最后要查询的区间是(son_u) 与 (v)之间的最大值

三、预处理

dfs1()

这个dfs要处理这四件事情：

1. 标记每个点的深度dep[ ]

2. 标记每个点的父亲fa[ ]

3. 标记每个非叶子节点的子树大小(含它自己)

4. 标记每个非叶子节点的重儿子编号son[ ]

void dfs1(int u,int fa)//u表示当前节点，fa表示当前节点的父亲
{
	f[u]=fa;//处理父亲
	siz[u]=1;//先标记
	son[u]=0;//最大的儿子
	dep[u]=dep[fa]+1;//处理深度
	for(int i=head[u];i!=0;i=e[i].nxt)
	{
		int v=e[i].to;
		if(v==fa) continue;//判重
		dfs1(v,u);siz[u]+=siz[v];
		if(siz[v]>siz[son[u]]) son[u]=v;//判断是否是重儿子
	}
}

dfs2()

这个dfs要处理这四件事情：

1. 标记每个点的新编号

2. 赋值每个点的初始值到新编号上

3. 处理每个点所在链的顶端

4. 处理每条链

顺序：先处理重儿子再处理轻儿子

(OneProblem)

为什么要先处理重儿子？

答：这样在后面我们所要处理的所有区间中点的编号(新编号) 均为连续的 ，这样方便我们建线段树。

建树

（其实就和线段树一样）

前面说到要用线段树，那么按题意建树就可以了。

不过需要注意的是，建树这一步要放在处理问题之前，不然(······)。

四、树剖

1、处理任意两点间路径时： 设所在链顶端的深度更深的那个点为x点

方法：

• ans加上x点到x所在链顶端 这一段区间的点权和

• 把x跳到x所在链顶端的那个点的上面一个点

不停执行这两个步骤，直到两个点处于一条链上，这时再加上此时两个点的区间和即可

这时我们注意到，我们所要处理的所有区间均为连续编号(新编号) ，于是想到线段树，用线段树处理连续编号区间和（为什么代码这么长？就因为这儿）

每次查询时间复杂度为(O(log^2n))，不错。

void Tupdate(int a,int b,int c,int flag)//树剖区间修改
{
	while(top[a]!=top[b])
	{
		if(dep[top[a]]<dep[top[b]]) swap(a,b);
		if(flag==1) update1(1,1,n,tid[top[a]],tid[a],c);
		else update2(1,1,n,tid[top[a]],tid[a],c);
		a=f[top[a]];
	}
	if(a==b) return;
	if(dep[a]>dep[b]) swap(a,b);
	if(flag==1) update1(1,1,n,tid[son[a]],tid[b],c);
	else update2(1,1,n,tid[son[a]],tid[b],c);
}

2、处理一点及其子树的点权和：

想到要记录每个非叶子节点的子树大小(含它自己)，并且每个子树的新编号都是连续的，然后直接线段树区间查询就行啦！！！时间复杂度为$ O(logn) $，很好

inline int qSon(int x)
{
    res=0;
    query(1,1,a,id[x],id[x]+siz[x]-1);//子树区间右端点id[x]+siz[x]-1 
    return res;
}

当然，区间修改是和区间查询一样的

int Tquery(int a,int b)//树剖区间查询
{
	int ans=-1e9;
	while(top[a]!=top[b])
	{
		if(dep[top[a]]<dep[top[b]])
		swap(a,b);
		ans=max(ans,query(1,1,n,tid[top[a]],tid[a]));
		a=f[top[a]];
	}
	if(a==b) return ans;
	if(dep[a]>dep[b]) swap(a,b);
	ans=max(ans,query(1,1,n,tid[son[a]],tid[b]));
	return ans;
}

五、代码

#include<bits/stdc++.h>
using namespace std;
using namespace std;
struct node{
	int to,nxt;
}e[200001];
int pos[100001],tid[100001],top[100001],dep[100001],son[100001],siz[100001],f[100001],head[100001];
int d[100001][5],sum[500001],col[200001],lzy[500001];
int n,m,cnt,cnt2;
void add(int u,int v)//加边函数，记得加双向
{
	e[++cnt].to=v;
	e[cnt].nxt=head[u];
	head[u]=cnt;
}
void dfs1(int u,int fa)//两个dfs初始化
{
	f[u]=fa;
	siz[u]=1;
	son[u]=0;
	dep[u]=dep[fa]+1;
	for(int i=head[u];i!=0;i=e[i].nxt)
	{
		int v=e[i].to;
		if(v==fa)
		continue;
		dfs1(v,u);siz[u]+=siz[v];
		if(siz[v]>siz[son[u]]) son[u]=v;
	}
}
void dfs2(int u,int tp)
{
	top[u]=tp;
	tid[u]=++cnt2;
	pos[cnt2]=u;
	if(son[u]) dfs2(son[u],tp);
	for(int i=head[u];i!=0;i=e[i].nxt)
	{
		int v=e[i].to;
		if(v==f[u]||v==son[u])
		continue;
		dfs2(v,v);
	}
}
void pushup(int id)
{
	sum[id]=max(sum[id<<1],sum[id<<1|1]);
}
void pushdown(int id)
{
	if(lzy[id]!=-1)
	{
		col[id<<1]=col[id<<1|1]=0;
		sum[id<<1]=sum[id<<1|1]=lzy[id];
		lzy[id<<1]=lzy[id<<1|1]=lzy[id];
		lzy[id]=-1;
	}
	if(col[id])
	{
		col[id<<1]+=col[id];
		col[id<<1|1]+=col[id];
		sum[id<<1]+=col[id];
		sum[id<<1|1]+=col[id];
		col[id]=0;
	}
}
void build(int id,int l,int r)
{
	lzy[id]=-1;
	if(l==r)
	return;
	int mid=(l+r)>>1;
	build(id<<1,l,mid);build(id<<1|1,mid+1,r);
	pushup(id);
}
void update1(int id,int l,int r,int x,int y,int z)//区间加数
{
	if(x<=l&&r<=y)
	{
		sum[id]+=z;
		col[id]+=z;
		return;
	}
	int mid=(l+r)>>1;
	pushdown(id);
	if(x<=mid) update1(id<<1,l,mid,x,y,z);
	if(y>mid) update1(id<<1|1,mid+1,r,x,y,z);
	pushup(id);
}
void update2(int id,int l,int r,int x,int y,int z)//区间覆盖
{
	if(x<=l&&r<=y)
	{
		sum[id]=z;
		lzy[id]=z;
		col[id]=0;
		return;
	}
	int mid=(l+r)>>1;
	pushdown(id);
	if(x<=mid) update2(id<<1,l,mid,x,y,z);
	if(y>mid) update2(id<<1|1,mid+1,r,x,y,z);
	pushup(id);
}
int query(int id,int l,int r,int x,int y)//区间查询
{
	if(x<=l&&r<=y)
	return sum[id];
	int mid=(l+r)>>1,ans=-1e9;
	pushdown(id);
	if(x<=mid) ans=max(ans,query(id<<1,l,mid,x,y));
	if(y>mid) ans=max(ans,query(id<<1|1,mid+1,r,x,y));
	return ans;
}
void Tupdate(int a,int b,int c,int flag)//树剖区间修改
{
	while(top[a]!=top[b])
	{
		if(dep[top[a]]<dep[top[b]]) swap(a,b);
		if(flag==1) update1(1,1,n,tid[top[a]],tid[a],c);
		else update2(1,1,n,tid[top[a]],tid[a],c);
		a=f[top[a]];
	}
	if(a==b) return;
	if(dep[a]>dep[b]) swap(a,b);
	if(flag==1) update1(1,1,n,tid[son[a]],tid[b],c);
	else update2(1,1,n,tid[son[a]],tid[b],c);
}
int Tquery(int a,int b)//树剖区间查询
{
	int ans=-1e9;
	while(top[a]!=top[b])
	{
		if(dep[top[a]]<dep[top[b]])
		swap(a,b);
		ans=max(ans,query(1,1,n,tid[top[a]],tid[a]));
		a=f[top[a]];
	}
	if(a==b) return ans;
	if(dep[a]>dep[b]) swap(a,b);
	ans=max(ans,query(1,1,n,tid[son[a]],tid[b]));
	return ans;
}
int main()//注：在这里我用了数组来存边，就不用乘以二了
{
	scanf("%d",&n);
	for(int i=1;i<n;i++)
	{
		scanf("%d%d%d",&d[i][0],&d[i][1],&d[i][2]);
		add(d[i][0],d[i][1]);
		add(d[i][1],d[i][0]);
	}
	dfs1(1,1);
	dfs2(1,1);
	build(1,1,n);
	for(int i=1;i<n;i++)
	{
		if(dep[d[i][0]]>dep[d[i][1]]) swap(d[i][0],d[i][1]);
		update1(1,1,n,tid[d[i][1]],tid[d[i][1]],d[i][2]);
	}
	while(1)
	{
		int a,b,c;
		char s[1001];
		scanf("%s",&s);
		if(s[0]=='S') return 0;
		else if(s[0]=='A')
		{
			scanf("%d%d%d",&a,&b,&c);
			Tupdate(a,b,c,1);
		}
		else if(s[1]=='o')
		{
			scanf("%d%d%d",&a,&b,&c);
			Tupdate(a,b,c,2);
		}
		else if(s[1]=='h')
		{
			scanf("%d%d",&a,&b);
			update2(1,1,n,tid[d[a][1]],tid[d[a][1]],b);
		}
		else if(s[0]=='M')
		{
			scanf("%d%d",&a,&b);
			printf("%d
",Tquery(a,b));
		}
	}
	return 0;
}

完美撒花！！！