莱文斯坦距离图解、算法实现与复杂度分析

编辑距离定义与分类

编辑距离的定义，直接引用百科：

编辑距离是針對二個字符串的差异程度的量化量测，量测方式是看至少需要多少次的处理才能将一个字符串变成另一个字符串。

编辑距离可以用在自然语言处理中，例如拼写检查可以根据一个拼错的字和其他正确的字的编辑距离，判断哪一个或几个是比较可能的字。

DNA也可以视为用A、C、G和T組成的字符串，因此编辑距离也用在生物信息学中，判断两个DNA的类似程度。

Unix下的 diff 和 patch 即是利用编辑距离来进行文本编辑对比的例子。

编辑距离有几种不同的定义，差异在于可以对字符串进行的处理的不同。其中比较常用的是莱文斯坦距离。

莱文斯坦（Levenshtein）距离，是编辑距离的一种。指两个字符串之间，只用如下允许的特定规则，由一个转成另一个所需的最少编辑操作次数。

允许的编辑操作包括：

1. 将一个字符替换成另一个字符

2. 插入一个字符

3. 刪除一个字符

莱文斯坦距离本质上可以理解为一个动态规划问题，其状态转移方程为：

解释一下状态转移方程：

1. 方程第一行：如果 min(i,j) = 0（即当前两个字符串至少有一个长度为0，即是空字符串）时，则此时的莱文斯坦距离就是两字符串的长度的最大值。这个很好理解，不赘述了

2. 方程第二行：如果min(i,j) != 0，则取如下三个数字的最小值：

2.1. 将a字符串的长度i减小1，计算其与长度为j的b字符串的莱文斯坦距离，并将其结果再加1，这其实等价于将当前a字符串的i位置的字符删除了；

2.2. 将b字符串的长度j减小1，计算其与长度为i的a字符串的莱文斯坦距离，并将其结果再加1，这其实等价于在当前a字符串的i位置后面插入了一个字符（即插入了b字符串j位置的那个字符）；

2.3. 将str_a、str_b字符串的长度同时减小1，计算两者的剩余字符串的莱文斯坦距离，此时如果str_a的i位置的字符和str_b的j位置的字符不同，则结果再加1，这其实等价于将str_a的i位置的字符改为str_b的j位置的那个字符；

莱文斯坦距离计算过程图解

以下通过一个例子来继续说明，假设当前要计算如下两个字符串的莱文斯坦距离：

str_a = "abcdd"

str_b = "ebcde"

可以通过绘制过程矩阵来直观地观察状态迁移方程是怎么工作的，如下表格的第一行表示str_a，第一列表示str_b，注意行与列的开头各自添加了一个0，表示空字符串

表格里一共有6*6=36个空白单元格，每个单元格中会记录下对应的行字符串和对应列字符串之间的莱文斯坦距离，例如下表所示：

单元格中应该记录：空字符串 与 ebcd 之间的莱文斯坦距离

单元格中应该记录：a 与 空字符串 之间的莱文斯坦距离

单元格中应该记录：abc 与 eb 之间的莱文斯坦距离

单元格中应该记录：abcdd 与 ebcdf 之间的莱文斯坦距离，这正好是题目本身，也就是说表格最右下角的单元格的值就是str_a和str_b的莱文斯坦距离。

好了，解释完基础概念后，现在来表格上演示如何推导出str_a和str_b的编辑距离。

按照状态转移方程，实际上可以从两个方向来解决，如果是从后往前推导，就是递归的思路；如果是从前往后推导，就是动态规划的思路。

从后往前推导（递归）

状态转换方程的表现形式就是递归方法，从后往前就是从结果单元格往回计算，找到获取结果所需要的依赖数值，然后再递归地计算每个依赖数值的依赖数值……

以表格中最右下角的蓝色单元格开始：

1. 其表示的是abcdd与ebcdf的距离，可见这俩字符串都不为空字符串，所以不符合状态转移方程的第一行，改走状态转移方程的第二行

2. 蓝色单元格的“左”、“上”、“左上”方的三个单元格，恰好就是对应状态转移方程第二行的三个分支：

2.1. 蓝色单元格“左”方的单元格，对应a字符串删除当前最后一个字符，再与b字符串计算距离；

2.2. 蓝色单元格“上”方的单元格，对应b字符串删除当前最后一个字符，再与a字符串计算距离；

2.3. 蓝色单元格“左上”方的单元格，对应a、b字符串各自删除当前最后一个字符，然后两个计算距离；

也就是说，如果想计算出蓝色单元格的数值，需要先知道3个橙色单元格的值。

而这3个橙色单元格的值，又可以递归地从他们对应的左、上、左上3个单元格的值计算得来：

        

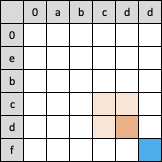
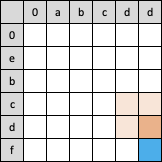
可见出现了递归现象，不断地重复重复，一直推算到表格的左上角，不能再推导了为止（碰到了空字符串） 

这种递归的解决方案有一个很大的问题就是冗余，重新观察一下上面3个表格示意图，如果把他们叠加到一起就会发现，有3个单元格各自被重复计算了2遍：

随着不断向左上角方向推导，这种重复计算的情况会越来越多，带来的问题就是做了大量的重复、冗余的工作，算法的时间复杂度变得非常高！

从前往后推导（动态规划）

总结上面遇到的问题的特点，就是将一个大问题拆解成多个小问题时，这些小问题彼此之间不独立，而是相互之间存在部分重复的计算。这种场景恰好是动态规划擅长解决的，因为动态规划是先从0开始，逐个计算出每个小的子问题的结果并将其记录下来，进而当计算到后面的大问题时，发现依赖到了之前的小问题的结果，直接查之前的小问题计算结果即可，因此动态规划是一种利用空间换时间的方法。

具体到上面的表格，就是从表格的左上角开始推导，逐步向右下方移动，当移动到最右下角时，即得到了最终答案。

1. 左上角单元格，表示的是两个空字符串的莱文斯坦距离，则根据状态转移方程，为max(0,0) = 0，所以该单元格的值是0：

2. 向右下方移动，顺次的两个单元格都直接依赖左上角单元格的结果，此时直接利用左上角单元格计算好的结果放到状态转移方程里(符合方程第一行的标准，即有一个字符串为空），即可得到这两个单元格的数值：

3. 顺次计算下面斜线方向的三个单元格，这里重点说一下红色框中空白单元格的计算，其符合状态转移方程的第二行即两个字符串a和e都不为空，所以要比较三个子字符串的最小值，上、左两个单元格的值都是1，这两个都需要再加1所以都是2，而左上单元格的值是0，且此时a和e不相同，需要再加1所以是1，最终基于左上角单元格的值计算下来的值（1）最小，所以此处填1——完全遵照状态转移方程推导了出来。

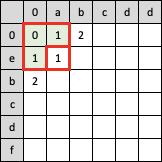
4. 以此类推，计算出每一个斜行的内容，最终得到了题目的答案：abcdd与ebcdf的莱文斯坦距离是2（第1个字符a替换为e、第5个字符d替换为f）

动态规划的方向

上面图示的动态规划的方向是从左上角到右下角，如果按照这种思路来编程，会发现需要对矩阵做斜向遍历，斜向遍历是可以做到的，但其比逐行、逐列遍历矩阵的成本要高。

再回看一下单元格的依赖关系，每个空白单元格依赖的是其左、上、左上 的3个单元格，所以其实不一定非要从左上往右下遍历，从左向右逐行遍历，或从上向下逐列遍历也没有问题。

即只要计算当前单元格的时候，能够获取到左、上、左上单元格的内容，那么这种遍历方式就是ok的

        

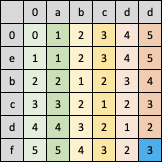
但逐行、逐列的遍历方式更容易写代码~；而斜向遍历要考虑很多异常情况，代码要复杂得多。

算法复杂度分析

时间复杂度

递归方法

递归方法因为存在大量的重复计算，所以时间复杂度非常高，这里没有想到好的详细推导证明的方法，粗略估计应该至少是个指数级的时间复杂度。

动态规划方法

动态规划从左上角依次计算每个单元格，因此是一个O(mn)的时间复杂度，可以看做是O(n²)；

空间复杂度

递归方法

递归方法的空间耗用主要体现在递归过程中对堆栈的使用上，虽然随着递归过程的深入需要不断入栈甚至有大量的冗余操作，但因为每条递归子路径计算完成后就会相应执行出栈动作，所以整体上栈空间的需求并不高

从右下角开始，亲自跟踪一下递归算法的入栈动作，会发现所需要的空间最多就是(m+1+n+1)，本质上就是矩阵右下角到左上角的曼哈顿距离。所以可以理解为递归算法的空间复杂度是O(m+n)。

动态规划方法

动态规划需要存储中间过程数值，假设使用数据等数据结构，则耗费的也是栈空间。动态规划需要将所有单元格的值存储下来，所以是O(mn)的空间复杂度，可以看做是O(n²)；

这里有一个空间复杂度的优化点：之前提到过：每个单元格都只依赖左、上、左上3个单元格，对其他更远的左/上方的单元格并不依赖，以从左至右逐行遍历举例，如下图所示：

 如果要计算红色框内的单元格，只需要3个蓝色框的单元格，其中左上、上的两个单元格是上一轮外循环计算的结果，左单元格是上一轮内循环计算的结果，所以我们只需要开辟一个S1 = m*2的矩阵，把上一轮和本轮外循环计算的结果都存储下来（即亮黄色背景的两行），循环结束后本轮结果替换上轮结果，然后继续迭代即可。这样空间复杂度可以缩减到O(m*2)，可以看做是O(n)；

代码实现

递归方法

递归方法代码很简单，完全遵从状态转移方程，直接上代码

#-*- encoding:utf-8 -*-
import sys


def levenshtein_distance(str_a, str_b):
    """莱文斯坦距离（递归实现）
    Args:
        str_a: 第一个字符串
        str_b: 第二个字符串
    return: 两个字符串的莱文斯坦距离
    exception:
        TypeError: 参数类型错误异常
    """
    # 异常类型判断
    if not isinstance(str_a, basestring) or not isinstance(str_b, basestring):
        raise TypeError("input must be string")

    # 判断空字符串
    if min(len(str_a), len(str_b)) == 0:
        return max(len(str_a), len(str_b))

    # 递归判断子串的距离
    ret_sub_a = levenshtein_distance(str_a[:-1], str_b) + 1
    ret_sub_b = levenshtein_distance(str_a, str_b[:-1]) + 1
    ret_sub_a_b = levenshtein_distance(str_a[:-1], str_b[:-1]) 
                + (1 if str_a[-1] != str_b[-1] else 0)
    return min(ret_sub_a, ret_sub_b, ret_sub_a_b)


def main(str_a, str_b):
    """主函数
    """
    print("distance=%d" % levenshtein_distance(str_a, str_b))


if __name__ == '__main__':
    main(sys.argv[1], sys.argv[2])

执行结果：

$ python levenshtein_distance_recursion.py abc 1
distance=3

动态规划方法

此处给出的是从左向右逐行遍历的代码实现

#-*- encoding:utf-8 -*-
import numpy as np
import sys

def levenshtein_distance(str_a, str_b):
    """莱文斯坦距离（动态规划实现）
    Args:
        str_a: 第一个字符串
        str_b: 第二个字符串
    return: 两个字符串的莱文斯坦距离
    exception:
        TypeError: 参数类型错误异常
    """
    if not isinstance(str_a, basestring) or not isinstance(str_b, basestring):
        raise TypeError("input must be string")

    len_a = len(str_a)
    len_b = len(str_b)

    # define a matrix variable
    matrix = np.zeros((len_a + 1, len_b + 1), dtype=int)
    
    # calculate distance between two strings recursively
    for i in range(0, len_a + 1):
        for j in range(0, len_b + 1):
            if min(i, j) == 0:
                matrix[i][j] = max(i, j)
                continue
            len_sub_a = matrix[i - 1][j] + 1
            len_sub_b = matrix[i][j - 1] + 1
            len_sub_a_b = matrix[i - 1][j - 1] + (1 if str_a[i - 1] != str_b[j - 1] else 0)
            matrix[i][j] = min(len_sub_a, len_sub_b, len_sub_a_b)

    return matrix[-1][-1]


def main(str_a, str_b):
    distance = levenshtein_distance(str_a, str_b)
    print("distance=%d" % distance)


if __name__ == '__main__':
    main(sys.argv[1], sys.argv[2])

 

执行结果：

$ python levenshtein_distance_dp.py abcdd ebcdf  
distance=2

进一步考虑优化空间复杂度的动态规划方法的代码实现（思路是申请一个两行n列的matrix，然后每轮内循环时往第1行里写入，内循环结束后把第1行的内容整体copy到第0行）

#-*- encoding:utf-8 -*-
import numpy as np
import sys

def levenshtein_distance(str_a, str_b):
    """莱文斯坦距离（动态规划实现+优化空间复杂度）
    Args:
        str_a: 第一个字符串
        str_b: 第二个字符串
    return: 两个字符串的莱文斯坦距离
    exception:
        TypeError: 参数类型错误异常
    """
    if not isinstance(str_a, basestring) or not isinstance(str_b, basestring):
        raise TypeError("input must be string")

    len_a = len(str_a)
    len_b = len(str_b)

    # define a matrix variable
    matrix = np.zeros((2, len_b + 1), dtype=int)
    
    # calculate distance between two strings recursively
    for i in range(0, len_a + 1):
        for j in range(0, len_b + 1):
            if min(i, j) == 0:
                matrix[1][j] = max(i, j)
                continue
            len_sub_a = matrix[0][j] + 1
            len_sub_b = matrix[1][j - 1] + 1
            len_sub_a_b = matrix[0][j - 1] + (1 if str_a[i - 1] != str_b[j - 1] else 0)
            matrix[1][j] = min(len_sub_a, len_sub_b, len_sub_a_b)
        matrix[0] = matrix[1].copy()

    return matrix[-1][-1]


def main(str_a, str_b):
    distance = levenshtein_distance(str_a, str_b)
    print("distance=%d" % distance)


if __name__ == '__main__':
    main(sys.argv[1], sys.argv[2])

当然，还可以进一步优化，省去copy的操作，用一个指示变量curr_i来控制当前写入的行：

#-*- encoding:utf-8 -*-
import numpy as np
import sys

def levenshtein_distance(str_a, str_b):
    """莱文斯坦距离（动态规划实现+优化空间复杂度）
    Args:
        str_a: 第一个字符串
        str_b: 第二个字符串
    return: 两个字符串的莱文斯坦距离
    exception:
        TypeError: 参数类型错误异常
    """
    if not isinstance(str_a, basestring) or not isinstance(str_b, basestring):
        raise TypeError("input must be string")

    len_a = len(str_a)
    len_b = len(str_b)

    # define a matrix variable
    matrix = np.zeros((2, len_b + 1), dtype=int)
    curr_i = 0 # only 0 or 1

    # calculate distance between two strings recursively
    for i in range(0, len_a + 1):
        for j in range(0, len_b + 1):
            if min(i, j) == 0:
                matrix[curr_i][j] = max(i, j)
                continue
            len_sub_a = matrix[1 - curr_i][j] + 1
            len_sub_b = matrix[curr_i][j - 1] + 1
            len_sub_a_b = matrix[1 - curr_i][j - 1] + (1 if str_a[i - 1] != str_b[j - 1] else 0)
            matrix[curr_i][j] = min(len_sub_a, len_sub_b, len_sub_a_b)
        curr_i = 1 - curr_i

    return matrix[1 - curr_i][-1]


def main(str_a, str_b):
    distance = levenshtein_distance(str_a, str_b)
    print("distance=%d" % distance)


if __name__ == '__main__':
    main(sys.argv[1], sys.argv[2])

执行结果

$ python levenshtein_distance_dp_opt.py abcdd dd
distance=3