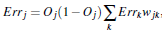下面开始正题
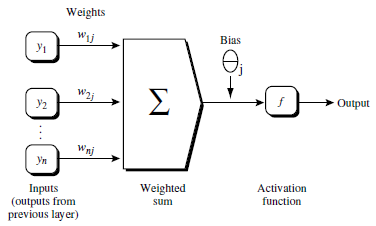
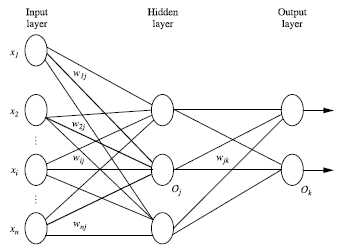
一、神经网络的构成
二、神经网络的算法的核心过程:
2.1. 前向传播求损失
由输入层向前传送

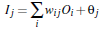

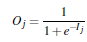
三、代码实现
3.1.定义激活函数
激活函数一般有双曲函数和逻辑函数
1.1 双曲函数(tanh)
其导数:
1.2 逻辑函数(logistic function)
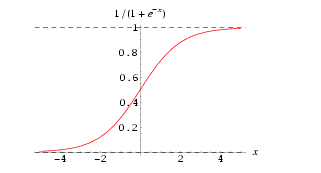
代码:
#!/usr/bin/env# -*- coding:utf-8 -*-import numpy as npdef tanh(x):return np.tanh(x)def tanh_derivative(x):return 1.0 - np.tanh(x) * np.tanh(x)def logistic(x):return 1 / (1 + np.exp(-x))def logistic_derivative(x):return logistic(x) * (1 - logistic(x) )
3.2 然后定义两层的神经网络的class,初始化激活函数,和权值:
给权值随机赋值,权值的范围[-0.25,0.25)
class NeuralNetworkWith2layers:def __init__(self, layers, activation='tanh'):if activation == 'Logistic':self.activation = logisticself.activation_deriv = logistic_derivativeelif activation == 'tanh':self.activation = tanhself.activation_deriv = tanh_derivativeself.weights = []for i in range(1, len(layers)-1):# 初始化 权值范围 [-0.25,0.25)# [0,1) * 2 - 1 => [-1,1) => * 0.25 => [-0.25,0.25)self.weights.append( (2*np.random.random((layers[i-1] + 1, layers[i] + 1 ))-1 ) * 0.25 )self.weights.append( (2*np.random.random((layers[i] + 1, layers[i+1] ))-1 ) * 0.25 )
3.3下面实现神经网络的核心训练逻辑向前传播计算损失和相互传播更新w
3.3.1、函数申明:
def fit(self, X, y, learning_rate=0.2, epochs = 10000):
参数X为样本数据,y为标签数据,learning_rate 为学习率默认0.2,epochs 为迭代次数默认值10000
3.3.2、数据预处理:
X = np.atleast_2d(X)X = np.column_stack((X, np.ones(len(X))))y = np.array(y)
上面代码,给X加了一个值为1的维度,y变成numpy中的array类型
3.3.3、数据训练
def fit(self, X, y, learning_rate=0.2, epochs = 10000):X = np.atleast_2d(X)temp = np.ones([X.shape[0], X.shape[1]+1])temp[:,0:-1] = XX = tempy = np.array(y)for k in range(epochs):i = np.random.randint(X.shape[0])a = [X[i]]# 正向计算for l in range(len(self.weights)):a.append(self.activation( np.dot(a[l], self.weights[l])) )# 反向传播error = y[i] - a[-1]deltas = [error * self.activation_deriv(a[-1])]# starting backprobagationlayerNum = len(a) - 2for j in range(layerNum, 0, -1): # 倒数第二层开始deltas.append(deltas[-1].dot(self.weights[j].T) * self.activation_deriv(a[j]))deltas.reverse()# 更新权值for i in range(len(self.weights)):layer = np.atleast_2d(a[i])delta = np.atleast_2d(deltas[i])self.weights[i] += learning_rate * layer.T.dot(delta)
正向计算部分:
将每层的计算节点值保存在二维数组a中,下面反向传播更新权值时候会用到该数据。计算过程如下图所示:

反向传播部分:
该部分的计算公式如下:
其中delta保存每层节点的Err值,最后利用前面的节点值a和现在的delta更新权值。
3.3.4、预测
预测的过程就是一个向前计算输出值的过程:
def predict(self, x):x = np.array(x)temp = np.ones(x.shape[0] + 1)temp[0:-1] = xa = tempfor l in range(0, len(self.weights)):a = self.activation(np.dot(a, self.weights[l]))return a
至此,神经网络的算法就完成了。大功告成!
四、神经网络代码测试
现在用刚才写的神经网络算法,来训练一个实现“异或“的神经网络。
输入数据如下:
0 0 0
0 1 1
1 0 1
1 1 0
前两列是x,最后一列是y
当x两个维度值是相同时候返回0,不同时候返回1,就是
“异或“。
代码如下:
#!/usr/bin/env# -*- coding:utf-8 -*-from NeuralNetwork import NeuralNetworkfrom DeepNeuralNetwork import DeepNeuralNetworkimport numpy as npnn = NeuralNetwork([2, 2, 1], 'tanh')#nn = DeepNeuralNetwork([2, 2, 1], 'tanh')x = np.array([[0,0],[0,1],[1,0],[1,1]])y = np.array([0,1,1,0])nn.fit(x, y)for i in [[0,0],[0,1],[1,0],[1,1]]:print (i, nn.predict(i))
执行结果:
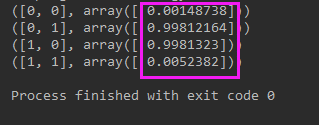
可以看到执行结果已经很不错了
五、后记
可以看到该神经网络的代码只是一个简单的两层网络,后面将继续改进实现更深层次的网络,可以关注本博客了解详情,敬请期待。
 、
、