Roberts算子
Roberts算子即为交叉微分算法,它是基于交叉差分的梯度算法,通过局部差分计算检测边缘线条。常用来处理具有陡峭的第噪声图像,当图像边缘接近于正45度或负45度时,该算法处理效果更理想,其缺点时对边缘的定位不太准确,提取的边缘线条较粗。
在Python中,Roberts算子主要是通过Numpy定义模板,再调用OpenCV的filter2D()函数实现边缘提取。该函数主要是利用内核实现对图像的卷积运算,其函数原型如下:
dst = filter2D(src, ddepth, kernel, dts, anchor,delta, borderType)
src:表示输入图像
ddepth: 表示目标图像所需的深度
kernel: 表示卷积核,一个单通道浮点型矩阵
anchor: 表示内核的基准点,其默认值为(-1, -1),位于中心位置
delta:表示在存储目标图像前可选的添加到像素的值,默认值为0
borderType:表示边框模式
import cv2 import numpy as np import matplotlib.pyplot as plt img = cv2.imread("src.png") img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB) grayImage = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY) # Roberts算子 kernelx = np.array([[-1, 0], [0, 1]], dtype=int) kernely = np.array([[0, -1], [1, 0]], dtype=int) x = cv2.filter2D(grayImage, cv2.CV_16S, kernelx) y = cv2.filter2D(grayImage, cv2.CV_16S, kernely) # 转转成uint8 absX = cv2.convertScaleAbs(x) absY = cv2.convertScaleAbs(y) Roberts = cv2.addWeighted(absX, 0.5, absY, 0.5, 0) # 正常显示中文标签 plt.rcParams["font.sans-serif"] = ["SimHei"] # 显示图形 titles = ["原始图像", "Roberts算子"] images = [img, Roberts] for i in range(2): plt.subplot(1, 2, i+1) plt.imshow(images[i], "gray") plt.title(titles[i]) plt.xticks([]) plt.yticks([]) plt.show()
效果如下:

Prewitt算子
Prewitt是一种图像边缘检测的微分算子,其原理是利用特定区域内像素值产生的差分实现边缘检测。由于Prewitt算子采用33模型对区域内的像素值进行计算,而Robert算子的模板为22,故Prewitt算子的边缘检测结果在水平/垂直方向均比Robert算子更加明显。Prewitt算子适合用来识别噪声较多,灰度渐变的图像。
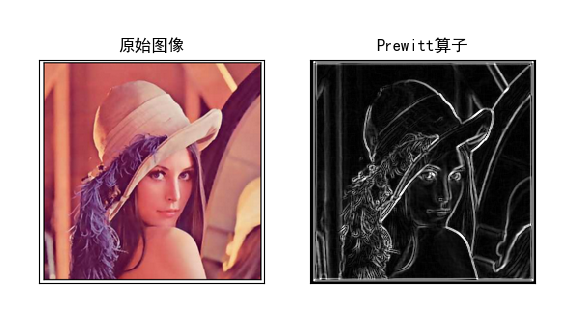
import cv2 import numpy as np import matplotlib.pyplot as plt img = cv2.imread("src.png") img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB) grayImage = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY) # Prewitt算子 kernelx = np.array([[1, 1, 1], [0, 0, 0], [-1, -1, -1]], dtype=int) kernely = np.array([[-1, 0, 1], [-1, 0, 1], [-1, 0, 1]], dtype=int) x = cv2.filter2D(grayImage, cv2.CV_16S, kernelx) y = cv2.filter2D(grayImage, cv2.CV_16S, kernely) # 转转成uint8 absX = cv2.convertScaleAbs(x) absY = cv2.convertScaleAbs(y) Roberts = cv2.addWeighted(absX, 0.5, absY, 0.5, 0) # 正常显示中文标签 plt.rcParams["font.sans-serif"] = ["SimHei"] # 显示图形 titles = ["原始图像", "Prewitt算子"] images = [img, Roberts] for i in range(2): plt.subplot(1, 2, i+1) plt.imshow(images[i], "gray") plt.title(titles[i]) plt.xticks([]) plt.yticks([]) plt.show()
效果如下:
Sobel算子
Sobel算子是一种用于边缘检测的离散的离散微分算子,它结合了高斯平滑和微分求导。该算子用于计算图像明暗程度近似值,根据图像边缘化旁边明暗程度把该区域内超过某个数的特定点记为边缘。Sobel算子在Prewitt算子的基础上增加了权重的概念,认为相邻点的距离远近对当前像素点的影响是不同的,距离越近的像素点对应当前像素的影响越大,从而实现图像锐化并突出边缘轮廓。
Sobel算子的边缘定位更准确,常用于噪声较多,灰度渐变的图像。
Sobel算法根据像素点上下,左右邻点灰度加权差,在边缘处达到极值这一现象检测边缘。对噪声具有平滑作用,提供较为精确的边缘方向信息。因为Sobel算子结合了高斯平滑和微分求导,因此结果会具有更多的抗噪性,当对精度要求不是很高时,Sobel算子是一种较为常用的边缘检测方法。
dst = Sobel(src, ddepth, dx, dy, dst,ksize, scale, delta, borderType)
src表示输入图像
dst表示输出的边缘图,其大小和通道数与输入图像相同
ddepth表示目标图像所需的深度,针对不同的输入图像,输出目标图像有不同的深度
dx表示x方向上的差分阶数,取值1或0
dy表示y方向上的差分阶数,取值1或0
ksize表示Sobel算子的大小,其值必须是正数和奇数
scale表示缩放导数的比例常数,默认情况下没有伸缩系数
delta表示将结果存入目标图像之前,添加到结果中的可选增量值
import cv2 import numpy as np import matplotlib.pyplot as plt img = cv2.imread("src.png") img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB) grayImage = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY) # Prewitt算子 # kernelx = np.array([[1, 1, 1], [0, 0, 0], [-1, -1, -1]], dtype=int) # kernely = np.array([[-1, 0, 1], [-1, 0, 1], [-1, 0, 1]], dtype=int) # x = cv2.filter2D(grayImage, cv2.CV_16S, kernelx) # y = cv2.filter2D(grayImage, cv2.CV_16S, kernely) x = cv2.Sobel(grayImage, cv2.CV_16S, 1, 0) y = cv2.Sobel(grayImage, cv2.CV_16S, 0, 1) # 转成uint8 absX = cv2.convertScaleAbs(x) absY = cv2.convertScaleAbs(y) Roberts = cv2.addWeighted(absX, 0.5, absY, 0.5, 0) # 正常显示中文标签 plt.rcParams["font.sans-serif"] = ["SimHei"] # 显示图形 titles = ["原始图像", "Sobel算子"] images = [img, Roberts] for i in range(2): plt.subplot(1, 2, i+1) plt.imshow(images[i], "gray") plt.title(titles[i]) plt.xticks([]) plt.yticks([]) plt.show()
效果如下:

Laplacian算子
拉普拉斯(Laplacian)算子是n维欧几里德空间中的一个二阶微分算子,常用于图像增强领域和边缘提取。它通过灰度差分计算邻域内的像素,基本流程是:判断图像中心像素灰度值与它周围其他像素的灰度值,如果中心像素的灰度更高,则提升中心像素的灰度;反之降低中心像素的灰度,从而实现图像锐化操作。在算法实现过程中,Laplacian算子通过对邻域中心像素的四方向或八方向求梯度,再将梯度相加起来判断中心像素灰度与邻域内其他像素灰度的关系,最后通过梯度运算的结果对像素灰度进行调整。
Python和OpenCV将Laplacian算子封装在Laplacian()函数中,其函数原型如下所示:
dst = Laplacian(src, ddepth[, dst[, ksize[, scale[, delta[, borderType]]]]])
src表示输入图像
dst表示输出的边缘图,其大小和通道数与输入图像相同
ddepth表示目标图像所需的深度
ksize表示用于计算二阶导数的滤波器的孔径大小,其值必须是正数和奇数,且默认值为1,更多详细信息查阅getDerivKernels
scale表示计算拉普拉斯算子值的可选比例因子。默认值为1,更多详细信息查阅getDerivKernels
delta表示将结果存入目标图像之前,添加到结果中的可选增量值,默认值为0
borderType表示边框模式,更多详细信息查阅BorderTypes
注意,Laplacian算子其实主要是利用Sobel算子的运算,通过加上Sobel算子运算出的图像x方向和y方向上的导数,得到输入图像的图像锐化结果。同时,在进行Laplacian算子处理之后,还需要调用convertScaleAbs()函数计算绝对值,并将图像转换为8位图进行显示。
当ksize=1时,Laplacian()函数采用3×3的孔径(四邻域模板)进行变换处理。下面的代码是采用ksize=3的Laplacian算子进行图像锐化处理,其代码如下:
import cv2 import numpy as np import matplotlib.pyplot as plt img = cv2.imread("src.png") img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB) grayImage = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY) # Roberts算子 # kernelx = np.array([[1, 1, 1], [0, 0, 0], [-1, -1, -1]], dtype=int) # kernely = np.array([[-1, 0, 1], [-1, 0, 1], [-1, 0, 1]], dtype=int) # x = cv2.filter2D(grayImage, cv2.CV_16S, kernelx) # y = cv2.filter2D(grayImage, cv2.CV_16S, kernely) # x = cv2.Sobel(grayImage, cv2.CV_16S, 1, 0) # y = cv2.Sobel(grayImage, cv2.CV_16S, 0, 1) # # 转转成uint8 # absX = cv2.convertScaleAbs(x) # absY = cv2.convertScaleAbs(y) dst = cv2.Laplacian(grayImage, cv2.CV_16S, ksize=3) dst = cv2.convertScaleAbs(dst) # 正常显示中文标签 plt.rcParams["font.sans-serif"] = ["SimHei"] # 显示图形 titles = ["原始图像", "Sobel算子"] images = [img, dst] for i in range(2): plt.subplot(1, 2, i+1) plt.imshow(images[i], "gray") plt.title(titles[i]) plt.xticks([]) plt.yticks([]) plt.show()
效果如下:

代码总结:
import cv2 import numpy as np import matplotlib.pyplot as plt img = cv2.imread("src.png") img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB) # 灰度处理 grayImage = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY) # 高斯波 gaussianBlur = cv2.GaussianBlur(grayImage, (3, 3), 0) # 阈值处理 ret, binary = cv2.threshold(gaussianBlur, 127, 255, cv2.THRESH_BINARY) # Roberts算子 kernelx = np.array([[-1, 0], [0, 1]], dtype=int) kernely = np.array([[0, -1], [1, 0]], dtype=int) x = cv2.filter2D(binary, cv2.CV_16S, kernelx) y = cv2.filter2D(binary, cv2.CV_16S, kernely) absX = cv2.convertScaleAbs(x) absY = cv2.convertScaleAbs(y) Roberts = cv2.addWeighted(absX, 0.5, absY, 0.5, 0) # Prewitt算子 kernelx = np.array([[1, 1, 1], [0, 0, 0], [-1, -1, -1]], dtype=int) kernely = np.array([[-1, 0, 1], [-1, 0, 1], [-1, 0, 1]], dtype=int) x = cv2.filter2D(binary, cv2.CV_16S, kernelx) y = cv2.filter2D(binary, cv2.CV_16S, kernely) absX = cv2.convertScaleAbs(x) absY = cv2.convertScaleAbs(y) Prewitt = cv2.addWeighted(absX, 0.5, absY, 0.5, 0) # Sobel算子 x = cv2.Sobel(binary, cv2.CV_16S, 1, 0) y = cv2.Sobel(binary, cv2.CV_16S, 0, 1) absX = cv2.convertScaleAbs(x) absY = cv2.convertScaleAbs(y) Sobel = cv2.addWeighted(absX, 0.5, absY, 0.5, 0) # Laplacian算子 dst = cv2.Laplacian(grayImage, cv2.CV_16S, ksize=3) dst = cv2.convertScaleAbs(dst) # 正常显示中文标签 plt.rcParams["font.sans-serif"] = ["SimHei"] # 显示图形 titles = ['Source Image', 'Binary Image', 'Roberts Image', 'Prewitt Image', 'Sobel Image', 'Laplacian Image'] images = [img, binary, Roberts, Prewitt, Sobel, dst] for i in range(6): plt.subplot(2, 3, i+1) plt.imshow(images[i], "gray") plt.title(titles[i]) plt.xticks([]) plt.yticks([]) plt.show()
效果如下:

Schar算子
由于Sobel算子在计算相对较小的时候,其近似计算导数的精度比较低,比如一个33的Sobel算子,当梯度角度接近水平或者垂直方向,其不精确性就越发明显。Scharr算子同Sobel算子的速度一样,但是精确度更高,尤其是计算较小核的情景,所以利用33滤波器实现图像边缘提取更推荐使用Scharr算子。
dst = Scharr(src, ddepth, dx, dy, dst, scale, delta, borderType)
src表示输入图像
ddepth表示输出目标图像所需的深度,针对不同的输入图像,输出目标图像有不同的深度
dx表示x方向上的差分阶数,取值1或者0
dy表示y方向上的差分阶数,取值0或者1
scale表示缩放导数的比例常数,默认情况下没有伸缩系数
delta表示将结果存入目标图像之前,添加到结果中的可选增量值
borderType表示边框模式
import cv2 import numpy as np import matplotlib.pyplot as plt img = cv2.imread("src.PNG") img = cv2.cvtColor(img, cv2.COLOR_RGB2BGR) grayImage = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY) # Scharr算子 x = cv2.Scharr(grayImage, cv2.CV_32F, 1, 0) y = cv2.Scharr(grayImage, cv2.CV_32F, 0, 1) absX = cv2.convertScaleAbs(x) absY = cv2.convertScaleAbs(y) scharr = cv2.addWeighted(absX, 0.5, absY, 0.5, 0) plt.rcParams["font.sans-serif"] = ["SimHei"] titles = ["原始图像", "Scharr算子"] images = [img, scharr] for i in range(2): plt.subplot(1, 2, i+1) plt.imshow(images[i], "gray") plt.title(titles[i]) plt.xticks([]) plt.yticks([]) plt.show()
效果如下:

转自:https://blog.csdn.net/Eastmount/article/details/89001702