图论-最短路
标签(空格分隔): @zhshh cpp OI 图论
最短路
BFS
思路
BFS也可以算作一个算法。在每步仅有相同的权重的寻路中应用。
比如每次走完一个队列,都相当与把最短距离为X的所有位置进行了试探。这样只要到了,那么一定是最短的。
代码
Floyd
思路
(O(N^3))算法。枚举每个起点,终点以及中间连线。
Dijkstra
#include <iostream>
#include <cstdio>
using namespace std;
#define MX 10000
#define INF 0x3f3f3f3f
struct node{
int v,nxt,w;
}edge[MX];
int head[MX];
int tot,n,m,x;
void add(int u,int v,int w){
tot++;
edge[tot].v=v;
edge[tot].w=w;
edge[tot].nxt=head[u];
head[u]=tot;
}
void init(){
int t1,t2,t3;
cin>>n>>m>>x;//n点,m边
memset(head,-1,sizeof(head));
for(int i=1;i<=m;i++){
cin>>t1>>t2>>t3;
add(t1,t2,t3);
}
}
void dijkstra(){
int dis[MX],vis[MX]={0};
int minj,mindis;
memset(dis,0x3f,sizeof(dis));
dis[x]=0;
for(int i=1;i<=n;i++){
mindis=0x3f3f3f3f;
minj=-1;
for(int j=1;j<=n;j++){
if(!vis[j]&&dis[j]<mindis){
mindis=dis[j];
minj=j;
}
}
// if(minj==-1){
// break;
// }
vis[minj]=1;
for(int j=head[minj];j!=-1;j=edge[j].nxt){
int v=edge[j].v;
if(!vis[v] && dis[v]>dis[minj]+edge[j].w){
dis[v]=mindis+edge[j].w;
}
}
}
for(int i=1;i<=n;i++)printf("%5d%5d
",i,dis[i]);
}
int main(){
init();
dijkstra();
}
区别
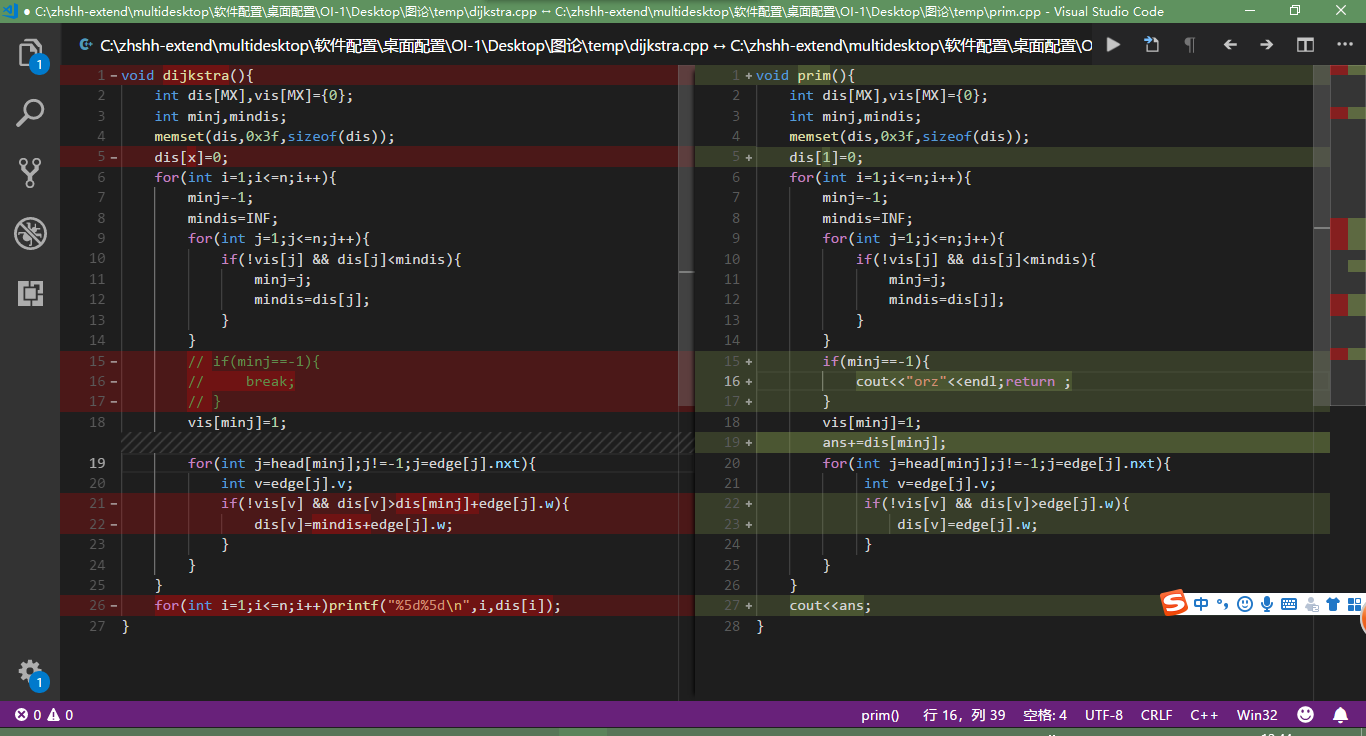
右面的prim是满行的。。所以行号根据prim来说了
Line5..dijkstra需要指定起点,而prim不用起点(任意一个都行,如果非要指定那么只当不是连通图时由于起点不同会跑到不同的树上,但是都能判断不连通)
Line15-17..都可以用来判断是否联通,,dijkstra其实不用注释掉也行(不过dijkstra在后面只要判断dis有没有==0x3f3f3f3f就行。不用break或者return了)
Line19..dijkstra是多节点都有不同的结果(dis[x],每个节点都有不同的距离)通过22-23行更新。而prim只有一个结果(最小树)而这个每次累加最小建立树枝成本。
Line22-23..从原理上分析
dijkstra是如果当前节点到minj+minj到x距离小于目前登记的dis[minj],那么更新成通过minj到x的最短距离
prim每次看的是最小建枝成本,即离树最近距离,因此更新为min(当前dis,距离minj距离)