PRML读书笔记——3 Linear Models for Regression

Linear Basis Function Models 

线性模型的一个关键属性是它是参数的一个线性函数，形式如下：

 w是参数，x可以是原始的数据，也可以是关于原始数据的一个函数值，这个函数就叫basis function，记作φ(x)，于是线性模型可以表示成：

 

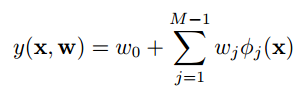
w₀看着难受，定义一个函数φ₀(x) = 1， 模型的形式再一次简化成：

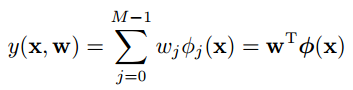
以上就是线性模型的一般形式。basis function有很多选择，例如Gaussian、sigmoid、tanh （tanh(x) = 2 * sigmoid(a) − 1）。

Maximum likelihood and least squares

训练线性模型的时候，假设cost function为sum-of-squares error function，那么minimize cost function 和 maximize likelihood function是等价的。

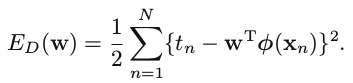
另外一个发现就是，w₀最终解出来为target values的均值 和 各个特征的basis function values均值的加权和 的差，如下：

 

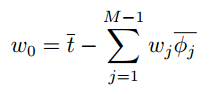
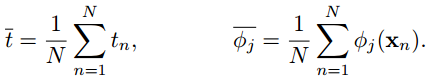
Regularized least squares

一般的正则化形式如下：

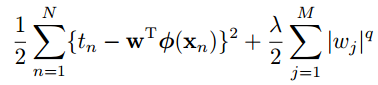
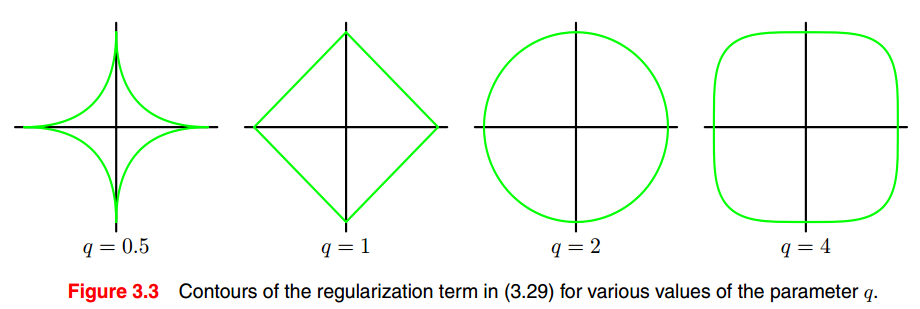
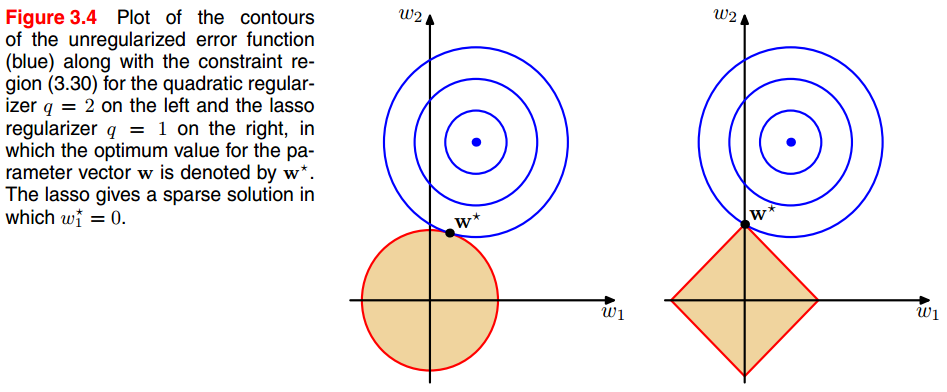
q = 1, 为lasso(least absolute shrinkage and selection operator) 正则化，其特点是，当λ足够大的时候，某些参数会趋向0，看下图。

q = 2, 二次正则化，使得一些参数足够小。

 

 

Bias-Variance trade-off

假设y(x, D)代表基于数据集D训练出来的regression function， h(x)代表数据集D中，给定x条件下target value的期望

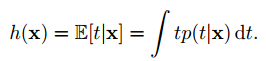
squared loss function可以写成：

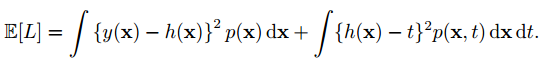
后一项与y(x)无关，考虑前一项积分里面的部分：

  {y(x; D) − h(x)}^{2 =}  {y(x; D) − E_D[y(x; D)] + E_D[y(x; D)] − h(x)}²

　　　　　　　　　　= {y(x; D) − E_D[y(x; D)]}² + {E_D[y(x; D)] − h(x)}²
　　　　　　　　　　　　+2{y(x; D) − E_D[y(x; D)]}{E_D[y(x; D)] − h(x)}

这样积分取期望后为：

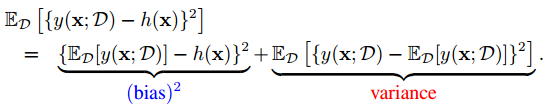
前一项为bias，后一项为variance。

于是loss function的总体希望就为，（bias）² + variance + noise

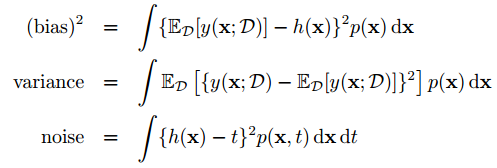
于是就产生了bias-variance trade-off问题， flexible models低bias，高variance；rigid models 高bias，低variance。

在实际应用中，为了观察bias和variance，计算如下：

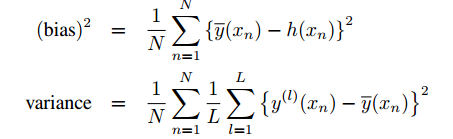
其中：

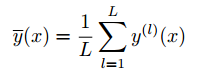
y^(l)(x)是prediction function。

Bayesian Linear Regression（该段摘自Jian Xiao（iamxiaojian@gmail.com）的笔记Notes on Pattern Recognition and Machine Learning (Bishop)）

Bayesian 方法能够避免 over-fitting 的原因是： Marginalizing over the model parameters instead of making point estimates of their values.

假设有多个 model；观察到的 data set 是 D。 Bayesian 的 model comparison 方法是，比较各个模型的后验概率，即：

 

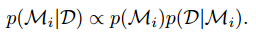
先验概率 p(M_i) allows us to express a preference for different model。可以假设每个模型的先验概率相等，那么剩下要比较的关键是： p(D|M_i) ——model evidence 或 marginal likelihood。

Model averaging V.S. model selection

Model averaging：把多个模型，用各自模型的后验概率加权平均，得到 predictive distribution为

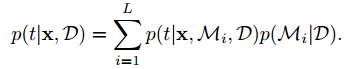
Model selection： 只选择一个模型，即其中后验概率最大的模型。这是一种 approximation to model averaging。以上分析可以看出，各个 model 的后验概率是关键，而计算后验概率的关键又是 model evidence。

从 sampling 的角度看， M_i 相当于 hyper-parameter，而 w 则是 parameter。 一个 model 不同于另一个 model，是因为 hyper-parameter。

The Evidence Approximation

full Bayesian需要marginalize with respect to hyper-parameters as well as parameters，例如hyperparameter是alpha和beta，w是parameter，那么predictive distribution为：

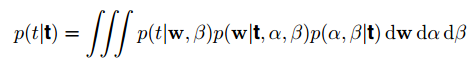
就比较难，这里就考虑一种approximation，给hyperparameters设置一个特定的数值，这个数值由maximizing the marginal likelihood function 来确定。这个方法叫empirical Bayes、 type 2 maximum likelihood、generalized maximum likelihood、evidence approximation(in machine learning)

Previous Chapter | Next Chapter