动手实现感知机算法，多分类问题

问题描述：

具有9个特征值的数据三分类问题，每个特征值的取值集合为{-1，0，1}。数据如下格式：

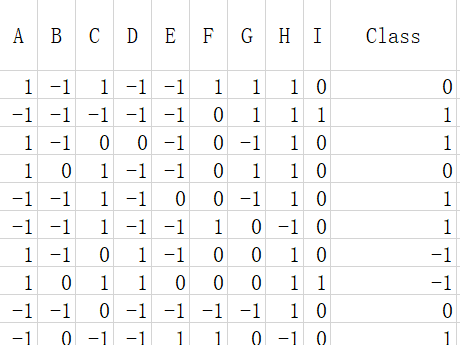
 设计感知机：

　　如何自己实现感知机的多分类，网上不调用库的资料非常少。之前有上算法课的时候，老师讲过多分类的神经网络，相比较于回归问题，多分类的损失函数设计时使用的是交叉熵。那么咱们按照这个思路从头推导下如何一步步迭代出权重值使得它们拟合出较好的效果来。

　　第一步：隐藏层设计，h = W*x + b（其中W为3*9矩阵，x为9维向量，b为3维向量）

 

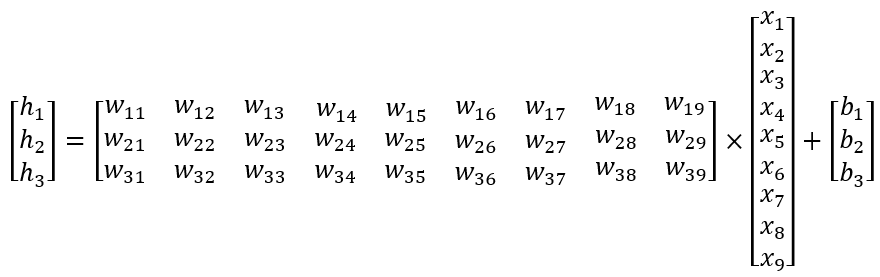
　　第二步：激活函数设计，a = softmax(h)（其中h为3维向量）

 

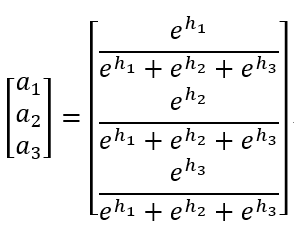
　　第三步：损失函数设计，Loss = y1lna1+y2lna2+y3lna3（其中a1,a2,a3,y1,y2,y3为单个数值）

 

权重值迭代：

 　　如何迭代权重值，以拟合我们的分类器。这里我们使用梯度下降算法，即W = W - lr*dLoss/dW，b = b - lr*dLoss/db，lr是超参，那么我们要求的就只有对W和b偏导。

代码实现：

 

import pandas as pd
import numpy as np
#数据集文件路径
file = 'Dataset.xlsx'

#获取训练集（原始训练集百分之八十）、验证集（原始训练集百分之二十）、测试集
def getData(filepath):
    df_train = pd.read_excel(filepath, sheet_name='training')
    df_test = pd.read_excel(filepath, sheet_name='test')
    length = len(df_train.values)
    x_train = df_train.values[:int(0.8 * length), :-1]
    y_train = df_train.values[:int(0.8 * length), -1]
    x_val = df_train.values[int(0.8 * length):, :-1]
    y_val = df_train.values[int(0.8 * length):, -1]
    x_test = df_test.values[:, :-1]
    return x_train, y_train, x_val, y_val, x_test


def main():
    #学习率
    lr = 0.000001
    # 类别一维转三维
    classMap = {'-1': [1, 0, 0],
                '0': [0, 1, 0],
                '1': [0, 0, 1]}
    #类别映射
    class_map = [-1, 0, 1]
    x_train, y_train, x_val, y_val, x_test = getData(file)
    #随机初始化W、b
    W = np.random.randn(3, 9)
    b = np.random.randn(3)
    #训练6000次
    for i in range(6000):
        loss = 0
        #初始化偏导
        alpha1 = [0] * 9
        alpha2 = [0] * 9
        alpha3 = [0] * 9
        beta1 = 0
        beta2 = 0
        beta3 = 0
        for xi, yi in zip(x_train, y_train):
            ai = np.sum(np.multiply([xi] * 3, W), axis=1) + b
            y_predicti = np.exp(ai) / sum(np.exp(ai))
            y_i = classMap[str(yi)]
            lossi = -sum(np.multiply(y_i, np.log(y_predicti)))
            loss += lossi
            # 每个训练数据偏导累加
            alpha1 += np.multiply(sum(np.multiply([0, 1, 1], y_i)), xi)
            alpha2 += np.multiply(sum(np.multiply([1, 0, 1], y_i)), xi)
            alpha3 += np.multiply(sum(np.multiply([1, 1, 0], y_i)), xi)
            beta1 += sum(np.multiply([0, 1, 1], y_i))
            beta2 += sum(np.multiply([1, 0, 1], y_i))
            beta3 += sum(np.multiply([1, 1, 0], y_i))
        #W、b更新值
        W[0] -= alpha1 * lr
        W[1] -= alpha2 * lr
        W[2] -= alpha3 * lr
        b[0] -= beta1 * lr
        b[1] -= beta2 * lr
        b[2] -= beta3 * lr
        loss = loss/len(x_train)
    recall = 0
    #验证
    for xi, yi in zip(x_val, y_val):
        ai = np.sum(np.multiply([xi] * 3, W), axis=1) + b
        y_predicti = np.exp(ai) / sum(np.exp(ai))
        y_predicti = [class_map[idx] for idx, i in enumerate(y_predicti) if i == max(y_predicti)][0]
        recall += 1 if int(y_predicti) == yi else 0
    print('验证集总条数：', len(x_val), '预测正确数：', recall)
    fp = open('perception.csv', 'w')
    #测试
    for xi in x_test:
        ai = np.sum(np.multiply([xi] * 3, W), axis=1) + b
        y_predicti = np.exp(ai) / sum(np.exp(ai))
        y_predicti = [class_map[idx] for idx, i in enumerate(y_predicti) if i == max(y_predicti)][0]
        fp.write(str(y_predicti)+'
')
    fp.close()

if __name__ == '__main__':
    print('方法三：感知机')
    main()