Anton and School

题意：给你一串只有‘（’与‘）’的字符串，问你多少对括号，括号一定是左边一半的‘（’，右边一半是‘）’

　　　）（（）（）   答案是：6

题解：枚举每个‘（’，此时设左括号左边有n个‘（’，它右边有m个‘）’，当我们设定此时的‘（’一定选定时，就不会重复了

　　　然后对于每个位置我们就可以推出这样的公式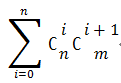：注意‘）’一定需要一个，且如果n<m则大于m的部分没有意义

　　　接着我们有范德蒙恒等式：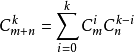

　　　我们可以这样理解：在m个人中选择i个，n个人选择k-i个人，则我们可以表示在m+n个人中选择k个人

　　　接着我们将原来的公式合并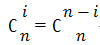：，然后可以将求和上面的n强行变成n+1，最后就可以展开使用阶层与逆元求出

　　　数据可以分开算，可以合起来计算

#include<set>
#include<map>
#include<queue>
#include<stack>
#include<cmath>
#include<vector>
#include<string>
#include<cstdio>
#include<cstring>
#include<iomanip>
#include<stdlib.h>
#include<iostream>
#include<algorithm>
using namespace std;
#define eps 1E-8
/*注意可能会有输出-0.000*/
#define sgn(x) (x<-eps? -1 :x<eps? 0:1)//x为两个浮点数差的比较,注意返回整型
#define cvs(x) (x > 0.0 ? x+eps : x-eps)//浮点数转化
#define zero(x) (((x)>0?(x):-(x))<eps)//判断是否等于0
#define mul(a,b) (a<<b)
#define dir(a,b) (a>>b)
typedef long long ll;
typedef unsigned long long ull;
const int Inf=1<<28;
const ll INF=1LL<<60;
const double Pi=acos(-1.0);
const ll Mod=1000000007LL;
const int Max=200010;
char str[Max];
ll fac[Max];//根据阶层求组合数
void exgcd(ll a,ll b,ll &d,ll &x,ll &y)//求逆元
{
    if(b==0LL)
    {
     x=1LL;
     y=0LL;
     d=a;
    }
    else
    {
        exgcd(b,a%b,d,y,x);
        y=(y-x*(a/b)%Mod+Mod)%Mod;
    }
    return;
}
void Init(int n)//初始化阶层
{
    fac[0]=1LL;
    for(int i=1;i<n;++i)
    {
        fac[i]=fac[i-1]*i%Mod;
    }
    return ;
}
ll Jud(ll n,ll m)//组合数公式
{
    ll d,x,y,res;
    exgcd(fac[n+1]*fac[m-1]%Mod,Mod,d,x,y);
    res=fac[n+m]*((x+Mod)%Mod)%Mod;
    return res;
}
int suml[Max],sumr[Max];
ll Solve(int n)
{
    ll ans=0LL;
    memset(suml,0,sizeof(suml));
    memset(sumr,0,sizeof(sumr));
    for(int i=0;i<n;++i)//前缀和
    {
        if(i)
        suml[i]=suml[i-1];
        if(str[i]=='(')
        {
            suml[i]++;
        }
    }
    for(int i=n-1;i>=0;--i)//后缀和
    {
        if(i<n-1)
            sumr[i]=sumr[i+1];
        if(str[i]==')')
        {
            sumr[i]++;
        }
    }
    for(int i=0;i<n;++i)
    {
        if(str[i]=='(')
        {
            ll n=suml[i]-1;//左边有左括号个数
            ll m=sumr[i];//右边有右括号个数
            if(m)
            ans=(ans+Jud(n,m))%Mod;
        }
    }
    return ans;
}
int main()
{
    int n;
    Init(Max);
    while(~scanf("%s",str))
    {
        n=strlen(str);
        printf("%I64d
",Solve(n));
    }
    return 0;
}