首先看抛物线函数：
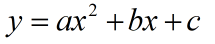
现在我取a=2,b=3,c=4 ,得到如下函数：
x或t都是指自变量，就不改了，一个意思。
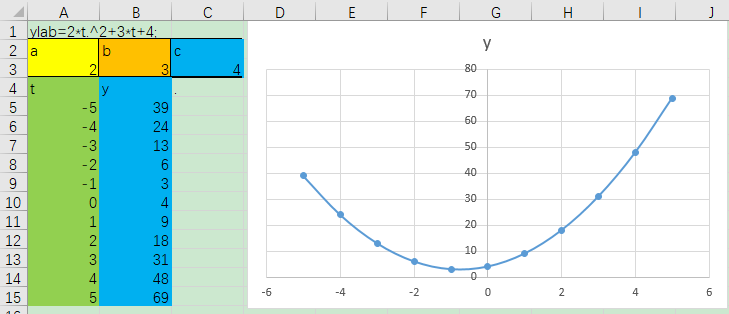
问题是，我想知道对于此数据和模型，参数a,b,c的敏感性，也就是y的改变量与a、b、c的改变量的比值关系。
- 首先用1stopt分析：
1 NewCodeBlock"SA"; 2 Parameter a=[1,3],b=[2,4],c=[3,5];//要优化的参数及其范围 3 Variable t,y;//变量 4 Function y=a*t^2+b*t+c; 5 Data; 6 //t y 变量顺序要和Variable后变量对应 7 -5 39 8 -4 24 9 -3 13 10 -2 6 11 -1 3 12 0 4 13 1 9 14 2 18 15 3 31 16 4 48 17 5 69
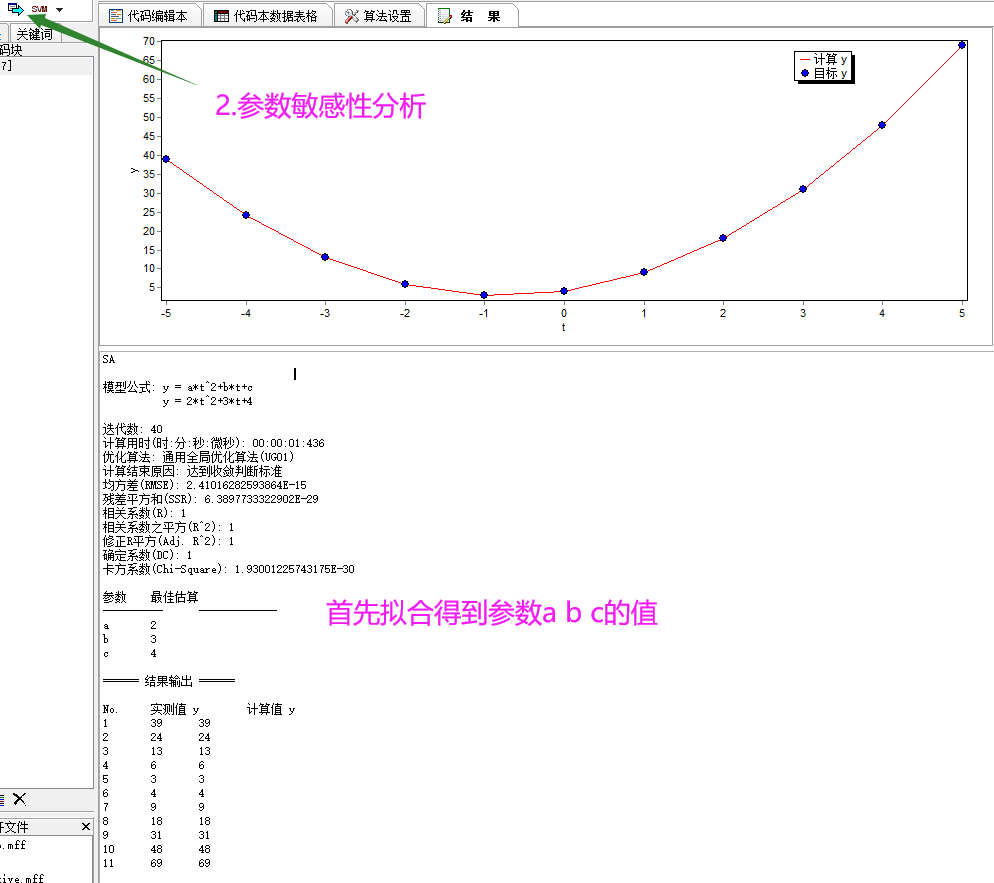
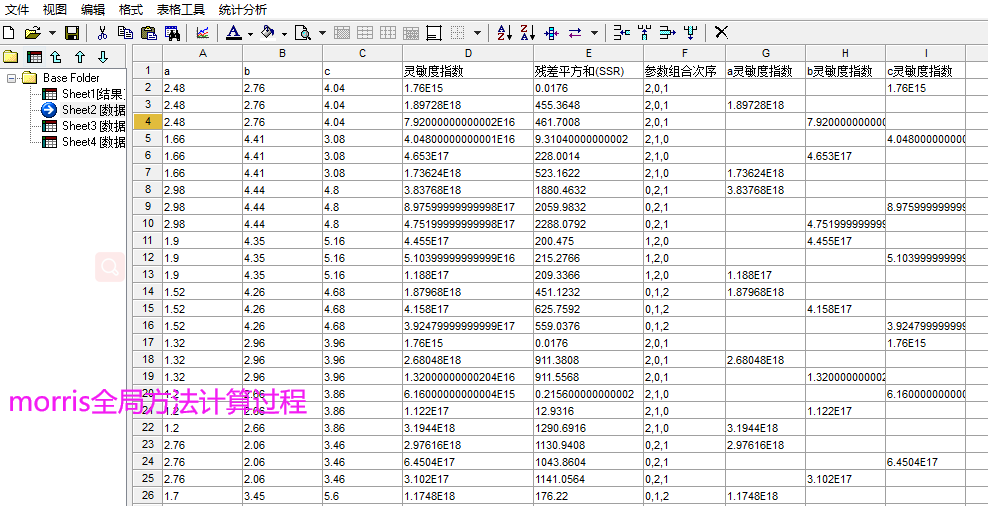
以下分别为各种参数敏感性方法（包括morris局部和全局，偏微分方法局部和全局）：
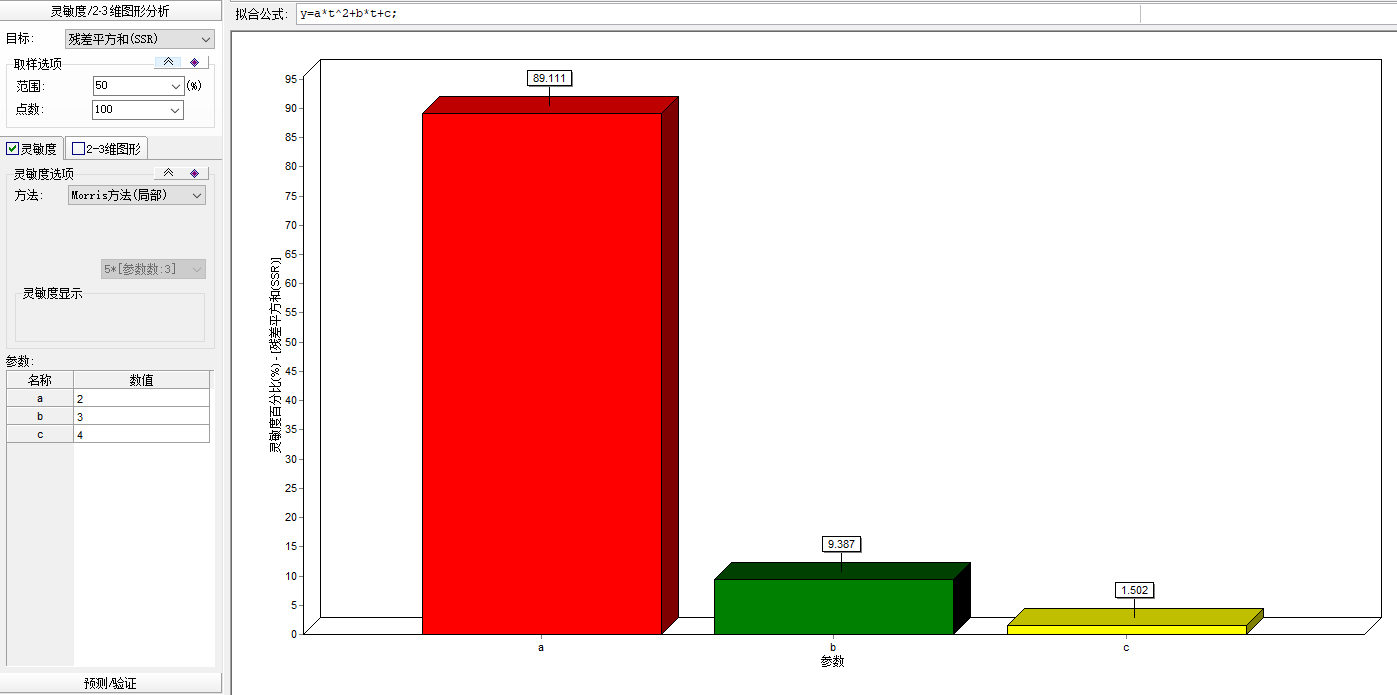
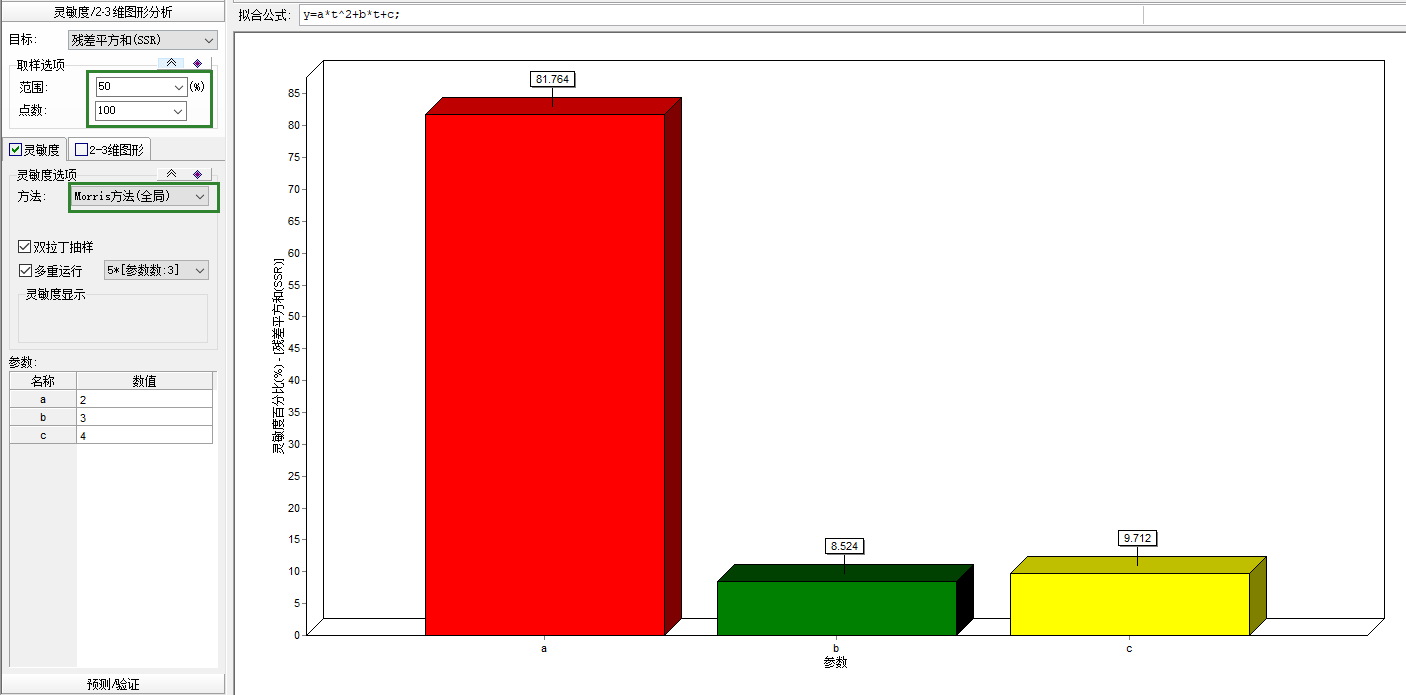
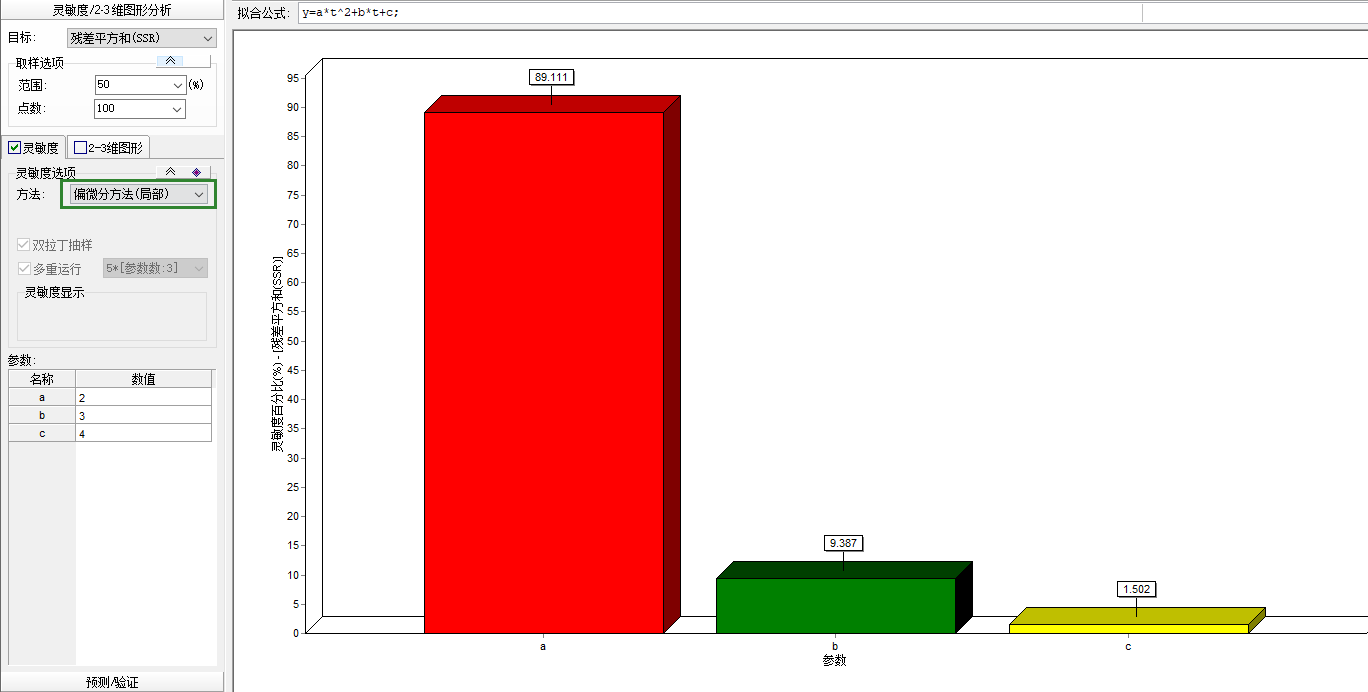
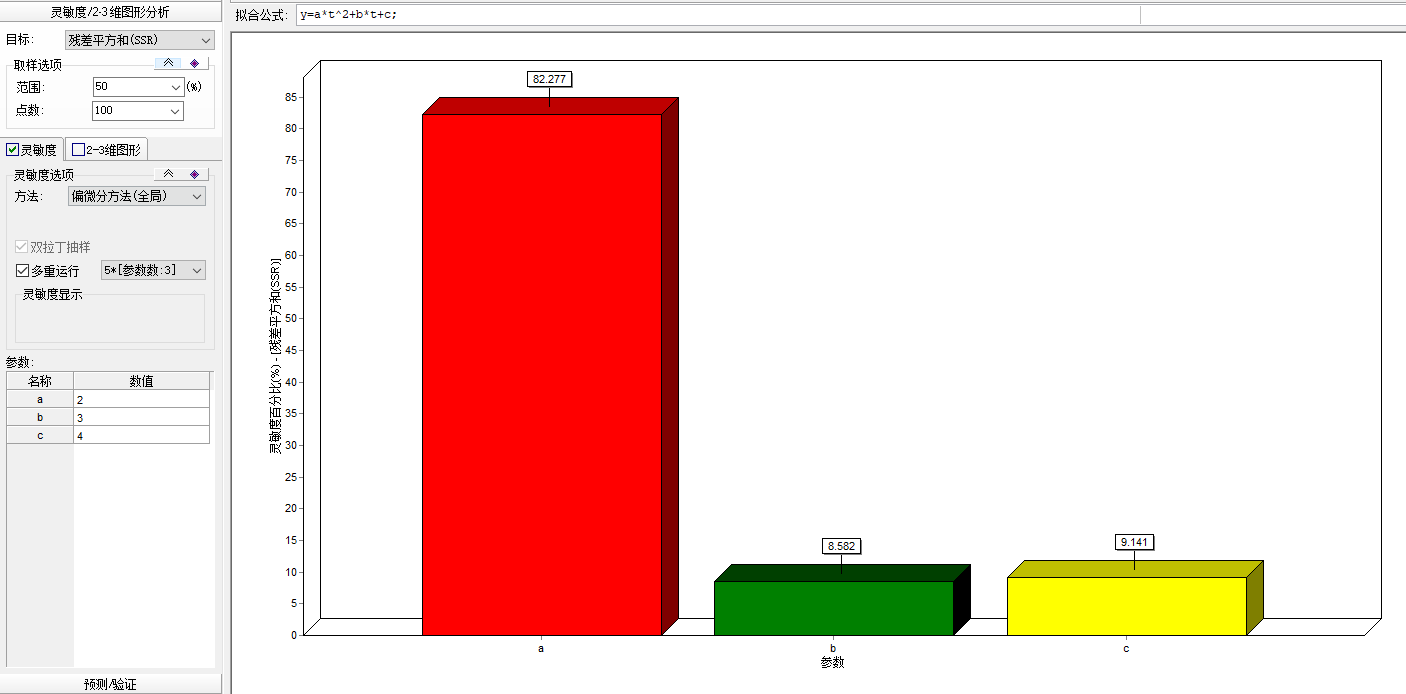
以上就是4中方法的结果。用的目标函数是SSR,点的范围我用的是上下浮动50%，正好布满整个给定空间：
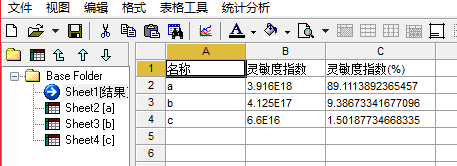
可以看morris局部敏感度分析具体数据：
a：
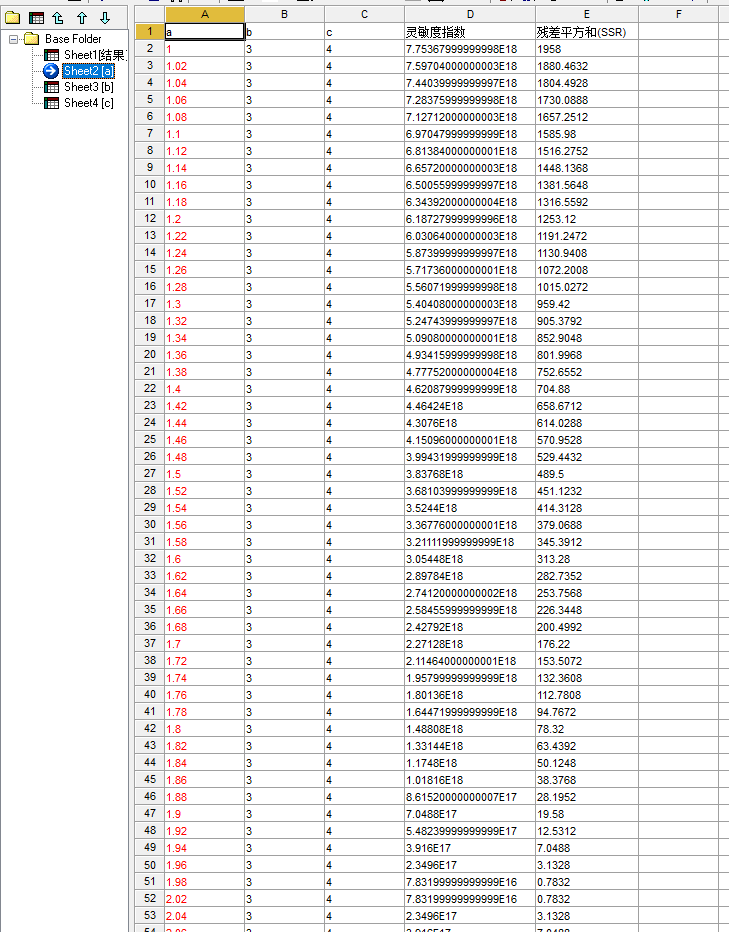
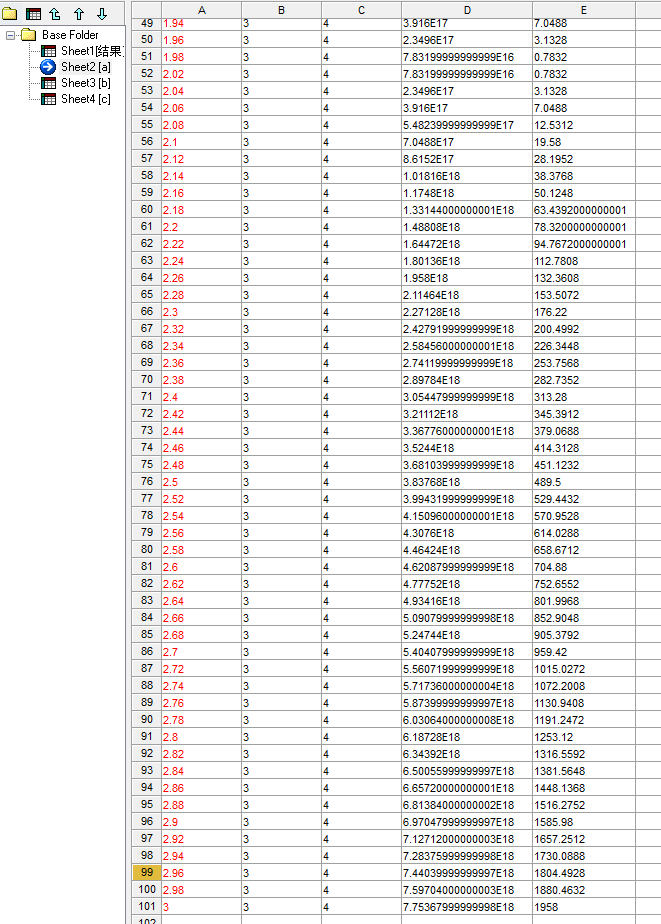
b：
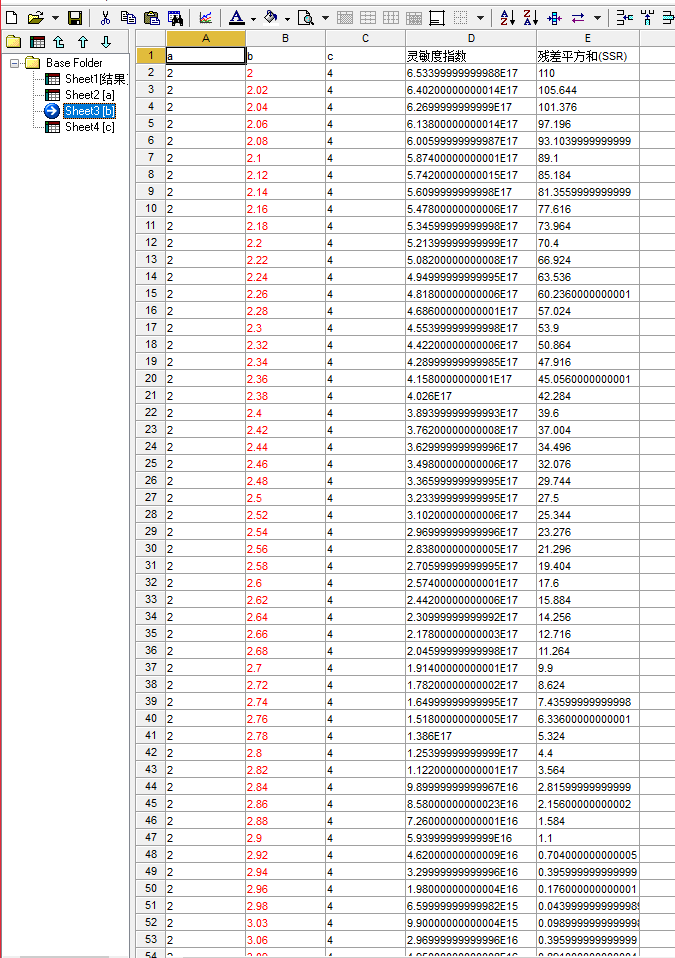
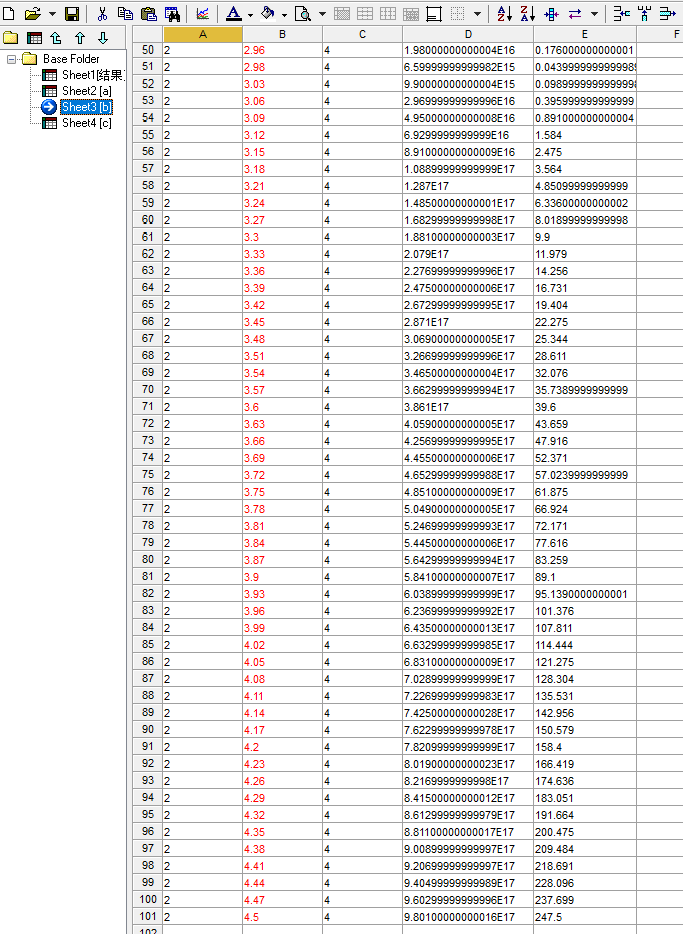
c：
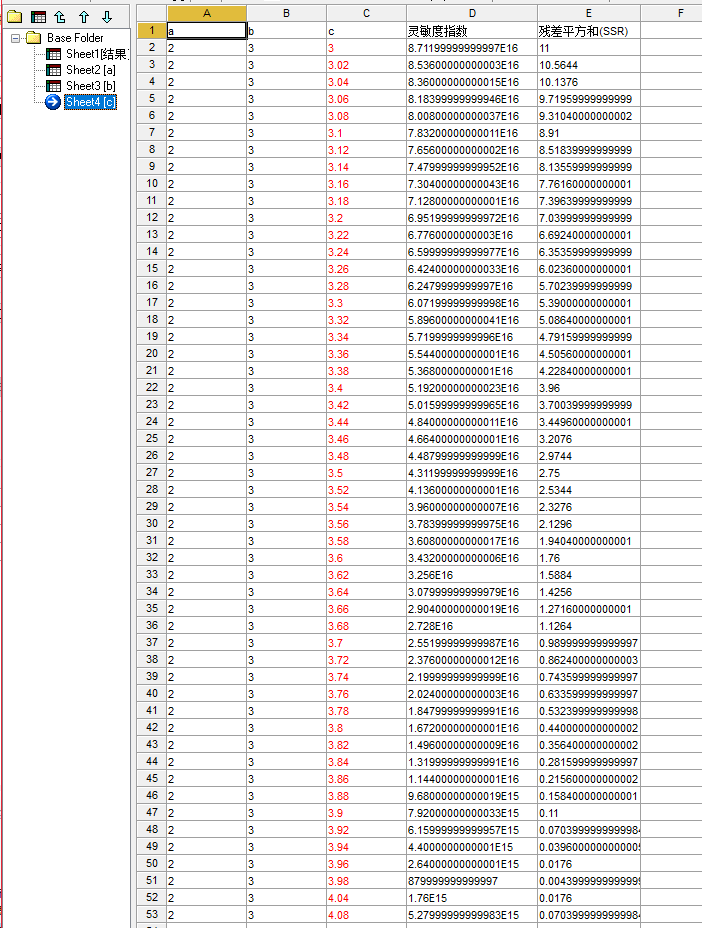
然后将灵敏度指数平均得到morris局部方法（本质是OAT方法，一次改变一个）分析结果：
全局方法（本质是通过拉丁抽样实现同时考虑多个参数的影响）就不是这个思路了，看一下超拉丁抽样：
总结一下1stopt中4种方法参数灵敏度结果：
morris方法局部：
名称 灵敏度指数 灵敏度指数(%)
a 3.916E18 89.1113892365457
b 4.125E17 9.38673341677096
c 6.6E16 1.50187734668335
morris方法全局：
名称 灵敏度指数 灵敏度指数(%)
a 2.00290323137447E18 81.4890482414753
b 2.10289523274038E17 8.55572692595605
c 2.44687506069835E17 9.95522483256862
偏微分方法局部：
名称 灵敏度指数 灵敏度指数(%)
a 3.99432000000567E18 89.1113892365577
b 4.20750000000213E17 9.38673341676365
c 6.73199999998753E16 1.50187734667864
偏微分方法全局：
名称 灵敏度指数 灵敏度指数(%)
a 3.98876054886661E18 82.084202339751
b 4.20542269921853E17 8.65428655186941
c 4.50049450186404E17 9.26151110837963
- 下面用matlab写sobol方法进行分析：
1 % sobol 参数敏感性分析 2 %算法参考： 3 % csdn : https://blog.csdn.net/xiaosebi1111/article/details/46517409 4 % wiki： https://en.wikipedia.org/wiki/Variance-based_sensitivity_analysis 具体参考文献这里也有 5 %运行环境 matlab2016b 6 %作者 blzhu@buaa.edu.cn 2020年6月7日 7 %% 初始化 8 clc; 9 clear all; 10 close all; 11 %% 设定：给定参数个数和各个参数的范围 12 13 % % 1-自定义子函数1 14 % D=3;% 维度3,几个参数 15 % nPop=4:500:5000;% 采样点个数,也就是参数水平数 ,取大了好，比如4000，但慢 16 % VarMin=[-pi -pi -pi ];%各个参数下限 SALib ：S1: [ 0.30797549 0.44776661 -0.00425452] ；ST: [0.56013728 0.4387225 0.24284474] 17 % VarMax=[pi pi pi];%各个参数上限 18 % myFunction=@(x) Ishigami(x);%目标函数，也可以是个黑盒子 19 20 % % 1-自定义子函数2 21 D=3;% 维度3,几个参数 22 nPop=4:50:1000;% 采样点个数,也就是参数水平数 ,取大了好，比如4000，但慢 23 VarMin=[1 2 3 ];%各个参数下限 24 VarMax=[3 4 5];%各个参数上限 25 myFunction=@(x) myx2(x); 26 27 % % 1-自定义子函数3 28 % D=4;% 维度3,几个参数 29 % nPop=4:50:1000;% 采样点个数,也就是参数水平数 ,取大了好，比如4000，但慢 30 % VarMin=[1 2 3 4];%各个参数下限 31 % VarMax=[3 4 5 5];%各个参数上限 32 % myFunction=@(x) myx3(x); 33 34 35 %% 开始计算 36 numnPop=numel(nPop); 37 SAll=zeros(numnPop,D+1);%分别是各参数的敏感度，最后一列是各参数敏感度之和 38 STAll=zeros(numnPop,D+1); 39 for i=1:numnPop 40 [S,ST]=sobol(D,nPop(i),VarMin,VarMax,myFunction); 41 SAll(i,1:D)=S'; 42 SAll(i,D+1)=sum(SAll(i,1:D)); 43 STAll(i,1:D)=ST'; 44 STAll(i,D+1)=sum(STAll(i,1:D)); 45 end 46 %% 绘图 47 color=[1 0 0;0 1 0;0 0 1;0.5 0.1 0;0 0.3 0.4;0.6 0.7 0.2;0.5 0.8 0.9;0 0.2 0.1;0.1 0.5 0;0.1 0 0.5;0.5 0 0.1];%12种颜色 一般颜色不一样 48 marker=['o','+','*','.','x','s','d','^','v','>','<','p','h'];%13种标记 一般标记也不一样; 字符数组，每个字符占1个位置 49 linestyle=[string('-'),string('--'),string(':'),string('-.'),string('none')]; 50 useL=1; 51 52 figure(1) 53 for i=1:D+1 54 plot(nPop,SAll(:,i),'Marker',marker(i),'LineStyle',char(linestyle(useL)),'Color',color(i,:),'LineWidth',1); 55 hold on 56 end 57 title('Sobol-S'); 58 whichPara=sprintfc('%g',repmat(1:D+1,1,2));%把数字数组转化成字符串数组 59 legend(whichPara,'Location','bestoutside');%加图例 60 61 62 figure(2) 63 for i=1:D+1 64 plot(nPop,STAll(:,i),'Marker',marker(i),'LineStyle',char(linestyle(useL)),'Color',color(i,:),'LineWidth',1); 65 hold on 66 end 67 title('Sobol-ST'); 68 whichPara=sprintfc('%g',repmat(1:D+1,1,2));%把数字数组转化成字符串数组 69 legend(whichPara,'Location','bestoutside');%加图例 70 71 disp('一阶影响指数（左方向收敛于1）Sobol-S：'); 72 disp(S); 73 disp('总效应指数（大于等于1，且仅当myfun是纯相加时取等号）Sobol-ST：'); 74 disp(ST); 75 disp(datetime); 76 disp('parameter sensitive analyse success use sobol method!'); 77 %% 火车声音提示已经算完了 78 load train 79 sound(y,Fs) 80 81 82 83 %% -------------------------子函数 matlab2016之前不支持子函数写在同一个m文档中---------------------------- 84 % 1-自定义子函数1（3个参数）Ishigami https://www.sfu.ca/~ssurjano/ishigami.html 85 function y=Ishigami(x) 86 y=sin(x(1))+7*(sin(x(2)))^2+0.1*x(3)^4*sin(x(1));% SALib用的这个 87 % y=sin(x(1))+7*(sin(x(2)))^2+0.05*x(3)^4*sin(x(1)); 88 end 89 90 % 1-自定义子函数2 （3个参数） 91 function y=myx2(x) 92 t=-5:1:5;%与此处有t范围和步距有关系 93 % t=-5:0.1:5;%与此处有t范围和步距有关系 94 ylab=2*t.^2+3*t+4; 95 ytheory=x(1)*t.^2+x(2)*t+x(3); 96 y=sum((ylab-ytheory).^2);%残差平方和SSR作为目标函数 97 % y=sum((ylab-ytheory).^2)/numel(t);%各参数灵敏度与上式相同 98 end 99 100 101 % 1-自定义子函数3（4个参数） 102 function y=myx3(x) 103 t=-5:1:5; 104 ylab=2*t.^3+3*t.^2+4*t+5; 105 ytheory=x(1)*t.^3+x(2)*t.^2+x(3)*t+x(4); 106 y=sum((ylab-ytheory).^2); 107 end 108 109 110 111 %% 2-求sobol敏感度 112 function [S,ST]=sobol(D,nPop,VarMin,VarMax,myFunction) 113 M=D*2;% 114 %% 产生所需的各水平参数 115 VarMin=[VarMin,VarMin]; 116 VarMax=[VarMax,VarMax]; 117 p= sobolset(M);% https://www.cnblogs.com/zhubinglong/p/12260292.html 118 % R=p(1:nPop,:);% 我只用前nPop个 119 R=[]; 120 for i=1:nPop 121 r=p(i,:); 122 r=VarMin+r.*(VarMax-VarMin); 123 R=[R; r]; 124 end 125 % plot(R(:,1),'b*') 126 % 拆分为A B 127 A=R(:,1:D);% 每行代表一组参数，其中每列代表每组参数的一个参数；行数就代表共有几组参数 128 B=R(:,D+1:end); 129 % 根据A B 产生矩阵AB 130 AB=zeros(nPop,D,D); 131 for i=1:D 132 tempA=A; 133 tempA(:,i)=B(:,i); 134 AB(1:nPop,1:D,i)=tempA; 135 end 136 %% 求各参数解 137 YA=zeros(nPop,1);% 解 138 YB=zeros(nPop,1); 139 YAB=zeros(nPop,D);%分别代表YAB1,YAB2,YAB3，YAB(:,D)就代表YABD 140 for i=1:nPop 141 YA(i)=myFunction(A(i,:)); 142 YB(i)=myFunction(B(i,:)); 143 for j=1:D 144 YAB(i,j)=myFunction(AB(i,:,j)); 145 end 146 end 147 %% 根据一阶影响指数公式： 148 VarX=zeros(D,1);% S的分子 149 S=zeros(D,1); 150 151 % 0: 估算基于给定样本的方差(EXCEL var.p) ; 1:计算基于给定的样本总体的方差(EXCEL var.p()) 152 % var([2.091363878 1.110366059 3.507651769 1.310950363 2.091363878 3.507651769 1.110366059 1.7066512],1); 153 VarY=var([YA;YB],1,'omitnan');% S的分母。 计算基于给定的样本总体的方差(EXCEL var.p()) 154 for i=1:D 155 for j=1:nPop 156 VarX(i)=VarX(i)+YB(j)*(YAB(j,i)-YA(j)); 157 end 158 VarX(i)=1/nPop*VarX(i);% 蒙特卡罗估计量 159 S(i)=VarX(i)/VarY; 160 end 161 162 %% 总效应指数 163 EX=zeros(D,1); 164 ST=zeros(D,1); 165 for i=1:D 166 for j=1:nPop 167 EX(i)=EX(i)+(YA(j)-YAB(j,i))^2; 168 end 169 EX(i)=1/(2*nPop)* EX(i);% 蒙特卡罗估计量 170 ST(i)=EX(i)/VarY; 171 end 172 end
我分别取了不同个数的样点 4:50:1000 ，结果如下，可见1000个样点基本稳定了。
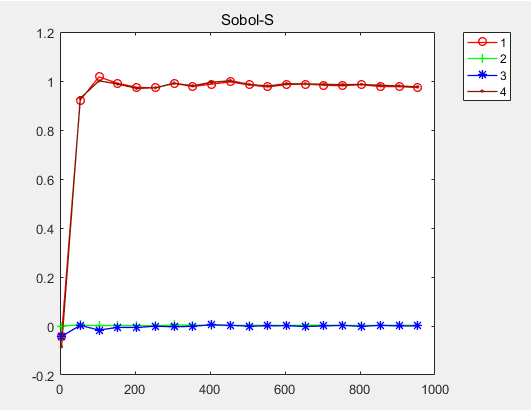
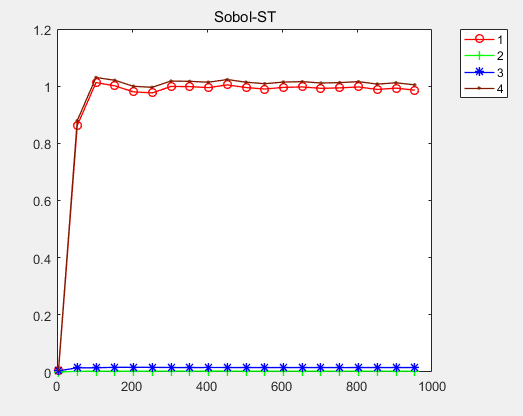
各参数的灵敏度：
一阶影响指数（左方向收敛于1）Sobol-S：
0.9728
0.0030
0.0001
总效应指数（大于等于1，且仅当myfun是纯相加时取等号）Sobol-ST：
0.9860
0.0031
0.0155
当然，也可以在matlab的fileexchange上下载各种工具箱，但这个根据csdn和wiki上写的算法相对简单些，便于魔改。
- 用python的SALib包分析
python中也有参数灵敏度分析的包SALib（https://salib.readthedocs.io/en/latest/index.html），这个包支持以下算法：
- Sobol Sensitivity Analysis ([Sobol 2001], [Saltelli 2002], [Saltelli et al. 2010])
- Method of Morris, including groups and optimal trajectories ([Morris 1991], [Campolongo et al. 2007])
- Fourier Amplitude Sensitivity Test (FAST) ([Cukier et al. 1973], [Saltelli et al. 1999])
- Random Balance Designs - Fourier Amplitude Sensitivity Test (RBD-FAST) ([`Tarantola et al. 2006 <https://hal.archives-ouvertes.fr/hal-01065897/file/Tarantola06RESS_HAL.pdf`_], [Elmar Plischke 2010], [Tissot et al. 2012])
- Delta Moment-Independent Measure ([Borgonovo 2007], [Plischke et al. 2013])
- Derivative-based Global Sensitivity Measure (DGSM) ([Sobol and Kucherenko 2009])
- Fractional Factorial Sensitivity Analysis ([Saltelli et al. 2008])
下面以sobol方法举例：
1 # https://salib.readthedocs.io/en/latest/basics.html#run-model 2 # -*- coding: utf-8 -*- 3 from SALib.sample import saltelli 4 from SALib.analyze import sobol 5 from SALib.test_functions import Ishigami 6 import numpy as np 7 import math 8 from SALib.plotting.bar import plot as barplot 9 import matplotlib.pyplot as plot 10 11 # problem = { 12 # 'num_vars': 3, 13 # 'names': ['x1', 'x2', 'x3'], 14 # 'bounds': [[-3.14159265359, 3.14159265359], 15 # [-3.14159265359, 3.14159265359], 16 # [-3.14159265359, 3.14159265359]] 17 # } 18 19 problem = { 20 'num_vars': 3, 21 'names': ['x1', 'x2', 'x3'], 22 'bounds': [[1, 3], 23 [2, 4], 24 [3, 5]] 25 } 26 27 28 param_values = saltelli.sample(problem, 1000)# 不管用哪个方法计算y,这个要有 29 np.savetxt("param_values.txt", param_values)# 将参数变化保存，其实是各参数范围内的sobol抽样 30 31 ## 计算Y 32 # #1-自定义-1 33 # Y = np.zeros([param_values.shape[0]]) 34 # A = 7 35 # B = 0.1 36 # for i, X in enumerate(param_values): 37 # Y[i] = math.sin(X[0]) + A * math.pow(math.sin(X[1]), 2) + 38 # B * math.pow(X[2], 4) * math.sin(X[0]) 39 40 #1-自定义-2 41 Y = np.zeros([param_values.shape[0]]) 42 for i, X in enumerate(param_values): 43 tarr=np.arange(-5,6,1); 44 yerror=0.0; 45 for t in tarr: 46 ylab=2*t**2+3*t+4; 47 ytheory=X[0]*t**2+X[1]*t+X[2]; 48 yerror=yerror+(ylab-ytheory)**2; 49 50 Y[i] = math.sqrt(yerror); 51 52 # 2-load计算好的txt 53 # Y = np.loadtxt("outputs.txt", float) 54 55 # 3-SALib自带测试函数 56 # Y = Ishigami.evaluate(param_values) 57 ## np.savetxt("outputs.txt", Y)#将因变量变化结果保存 58 59 Si = sobol.analyze(problem, Y ,print_to_console=True) 60 print()#自动输出S1（单个参数对因变量的影响）、ST（考虑各个变量相互影响）和S2(两两参数之间影响)，需有,print_to_console=True 61 62 print("all parameters first-order sensitivity indices S1:") 63 print(Si['S1'])# 一阶影响指数 64 print("all parameters second-order sensitivity indices S2:") 65 print(Si['S2'])#二阶影响指数 66 print("all parameters total sensitivity indices ST:") 67 print(Si['ST'])# 总效应指数 68 69 #绘图 https://zhuanlan.zhihu.com/p/137953265 70 Si_df = Si.to_df() 71 barplot(Si_df[0]) 72 plot.show()
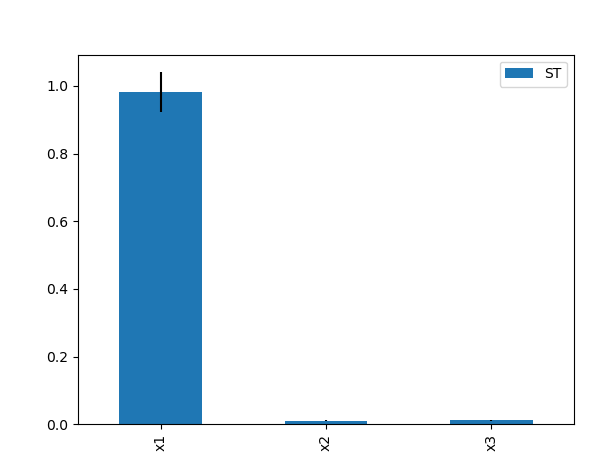
输出结果：
Parameter S1 S1_conf ST ST_conf
x1 0.969397 0.069624 0.982232 0.058139
x2 0.007222 0.009055 0.009680 0.001325
x3 0.000848 0.008468 0.011699 0.001033
Parameter_1 Parameter_2 S2 S2_conf
x1 x2 0.000330 0.070070
x1 x3 0.010014 0.069389
x2 x3 -0.000129 0.013788
all parameters first-order sensitivity indices S1:
[9.69397123e-01 7.22243327e-03 8.47690887e-04]
all parameters second-order sensitivity indices S2:
[[ nan 0.00032978 0.01001386]
[ nan nan -0.00012935]
[ nan nan nan]]
all parameters total sensitivity indices ST:
[0.9822323 0.00968001 0.01169928]
也可以用morris方法：
只需要导入
from SALib.analyze import morris
然后用
Si = morris.analyze(problem, Y ,print_to_console=True) 代替
python3.8.1+SALib1.3 use morris
Si = sobol.analyze(problem, Y ,print_to_console=True)
1 # https://salib.readthedocs.io/en/latest/basics.html#run-model 2 # -*- coding: utf-8 -*- 3 from SALib.sample import saltelli 4 from SALib.analyze import sobol 5 from SALib.analyze import morris 6 from SALib.test_functions import Ishigami 7 import numpy as np 8 import math 9 from SALib.plotting.bar import plot as barplot 10 import matplotlib.pyplot as plot 11 12 # problem = { 13 # 'num_vars': 3, 14 # 'names': ['x1', 'x2', 'x3'], 15 # 'bounds': [[-3.14159265359, 3.14159265359], 16 # [-3.14159265359, 3.14159265359], 17 # [-3.14159265359, 3.14159265359]] 18 # } 19 20 problem = { 21 'num_vars': 3, 22 'names': ['x1', 'x2', 'x3'], 23 'bounds': [[1, 3], 24 [2, 4], 25 [3, 5]] 26 } 27 28 29 param_values = saltelli.sample(problem, 1000)# 不管用哪个方法计算y,这个要有 30 np.savetxt("param_values.txt", param_values)# 将参数变化保存，其实是各参数范围内的sobol抽样 31 32 ## 计算Y 33 # #1-自定义-1 34 # Y = np.zeros([param_values.shape[0]]) 35 # A = 7 36 # B = 0.1 37 # for i, X in enumerate(param_values): 38 # Y[i] = math.sin(X[0]) + A * math.pow(math.sin(X[1]), 2) + 39 # B * math.pow(X[2], 4) * math.sin(X[0]) 40 41 #1-自定义-2 42 Y = np.zeros([param_values.shape[0]]) 43 for i, X in enumerate(param_values): 44 tarr=np.arange(-5,6,1); 45 yerror=0.0; 46 for t in tarr: 47 ylab=2*t**2+3*t+4; 48 ytheory=X[0]*t**2+X[1]*t+X[2]; 49 yerror=yerror+(ylab-ytheory)**2; 50 51 Y[i] = math.sqrt(yerror); 52 53 # 2-load计算好的txt 54 # Y = np.loadtxt("outputs.txt", float) 55 56 # 3-SALib自带测试函数 57 # Y = Ishigami.evaluate(param_values) 58 ## np.savetxt("outputs.txt", Y)#将因变量变化结果保存 59 60 # Si = sobol.analyze(problem, Y ,print_to_console=True) 61 Si = morris.analyze(problem, Y ,print_to_console=True) 62 print()#自动输出S1（单个参数对因变量的影响）、ST（考虑各个变量相互影响）和S2(两两参数之间影响)，需有,print_to_console=True 63 64 print("all parameters first-order sensitivity indices S1:") 65 print(Si['S1'])# 一阶影响指数 66 print("all parameters second-order sensitivity indices S2:") 67 print(Si['S2'])#二阶影响指数 68 print("all parameters total sensitivity indices ST:") 69 print(Si['ST'])# 总效应指数 70 71 #绘图 https://zhuanlan.zhihu.com/p/137953265 72 Si_df = Si.to_df() 73 barplot(Si_df[0]) 74 plot.show()
Parameter S1 S1_conf ST ST_conf
x1 0.969397 0.072129 0.982232 0.062795
x2 0.007222 0.008033 0.009680 0.001303
x3 0.000848 0.009519 0.011699 0.001045
Parameter_1 Parameter_2 S2 S2_conf
x1 x2 0.000330 0.087924
x1 x3 0.010014 0.087743
x2 x3 -0.000129 0.013700
all parameters first-order sensitivity indices S1:
[9.69397123e-01 7.22243327e-03 8.47690887e-04]
all parameters second-order sensitivity indices S2:
[[ nan 0.00032978 0.01001386]
[ nan nan -0.00012935]
[ nan nan nan]]
all parameters total sensitivity indices ST:
[0.9822323 0.00968001 0.01169928]
小技巧：
SALib如果不便于将目标函数写为函数的形式，可以将代码：
np.savetxt("param_values.txt", param_values)# 将参数变化保存，其实是各参数范围内的sobol抽样
生成的抽样带入自己的系统，然后根据自己需要生成对应抽样的目标函数，将目标函数放入同目录下的 outputs.txt 文档中，一行一个结果，然后用这个语句代替上面求Y[i]:
Y = np.loadtxt("outputs.txt", float)
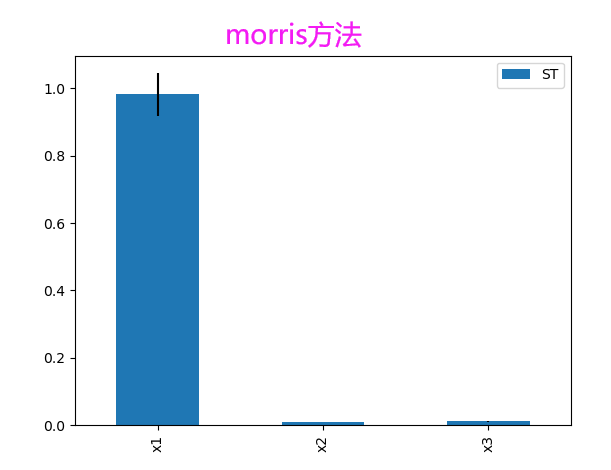
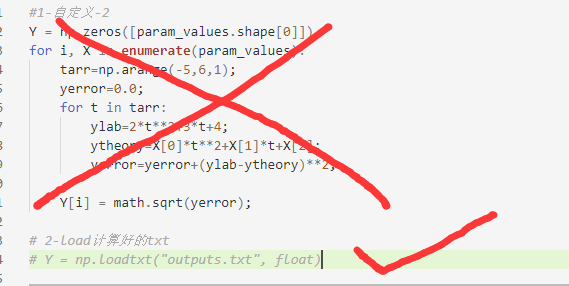
就是说提供了参数变化以及目标函数变化，用SALib就可以求参数灵敏度了。
总结：
matlab我用的sobol生成的抽样和别人的不一样，不知道为什么，这个是造成与python计算不一样的一个原因吧。但差别不大。
灵敏度分析的概念在此处没有详细讲，可以参考：https://en.wikipedia.org/wiki/Variance-based_sensitivity_analysis