【LeetCode】克隆图

【问题】给定无向连通图中一个节点的引用，返回该图的深拷贝（克隆）。图中的每个节点都包含它的值 val（Int） 和其邻居的列表（list[Node]）。

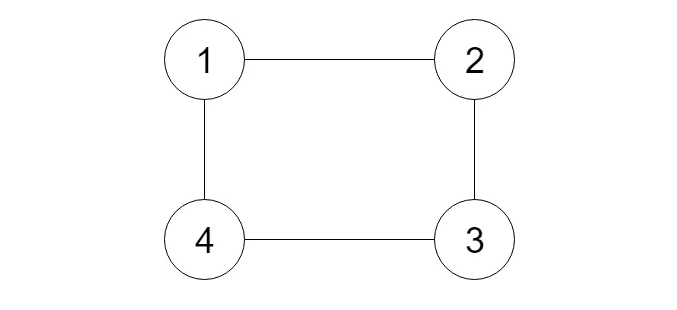
解释：
节点 1 的值是 1，它有两个邻居：节点 2 和 4 。
节点 2 的值是 2，它有两个邻居：节点 1 和 3 。
节点 3 的值是 3，它有两个邻居：节点 2 和 4 。
节点 4 的值是 4，它有两个邻居：节点 1 和 3 。

提示：

• 节点数介于 1 到 100 之间。

• 无向图是一个简单图，这意味着图中没有重复的边，也没有自环。

• 由于图是无向的，如果节点 p 是节点 q 的邻居，那么节点 q 也必须是节点 p 的邻居。

• 必须将给定节点的拷贝作为对克隆图的引用返回。

【思路】克隆图，并且是无向连通图，因此可以使用map来保存两个节点之间的连接关系，如果在map中没有该节点tmp，则新建节点tmp_copy将该节点存入map中，然后遍历该节点的所有邻居，并递拷贝其所有邻居节点至tmp_copy的邻居数组中。

/*
// Definition for a Node.
class Node {
public:
    int val;
    vector<Node*> neighbors;

    Node() {}

    Node(int _val, vector<Node*> _neighbors) {
        val = _val;
        neighbors = _neighbors;
    }
};
*/
class Solution {
public:
    map<Node*,Node*> mp;
    Node* cloneGraph(Node* node) {
        if(!node)   return nullptr;
        if(mp.count(node))  return mp[node];  // 如果存在，就不用新建了
        Node* tmp = new Node(node -> val);
        mp[node] = tmp;
        for(int i = 0; i < node -> neighbors.size(); ++ i){
            if(node -> neighbors[i])    tmp -> neighbors.push_back(cloneGraph(node -> neighbors[i]));
        }
        return tmp;
    }
};