然后废话:
这道题是一道很神奇的dfs?(算是吧)然后是wxl学长讲的;
SOLUTION:
首先解释一下对称二叉树:
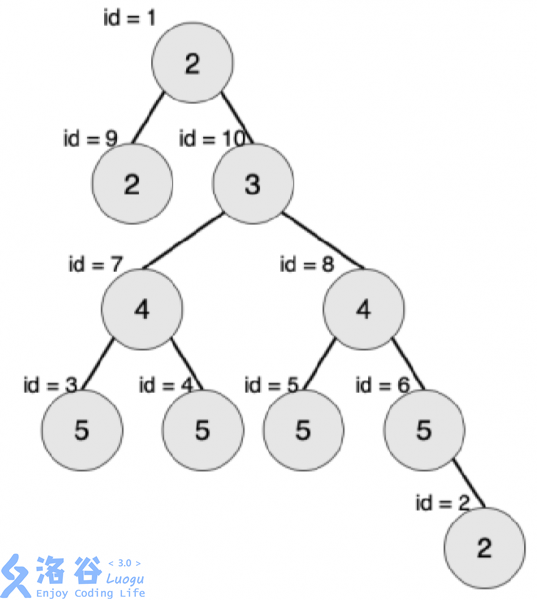
你看这棵树,最大的对称二叉树节点数为3,然后可能会误会成id 8,5,6,但是实际上指的是id 7,3,5。因为对称二叉树的要求是:
将这棵树所有节点的左右子树交换,新树和原树对应位置的结构相同且点权相等。
可以理解为轴对称;
好了没有然后了(jiushiweilecougezishu)
首先是读入,因为是二叉树,所以直接存左右鹅子开一个二维数组,第二维0表示左儿子,1表示右儿子。然后分别读入就好啦。
大框架:
memset(son,-1,sizeof(son));
读入:
……
dfs(1);
枚举以每个点为根的子树;
如果满足对称二叉树的要求,与当前最大值比较,取更大的那个;
输出;
然后是dfs记录每个子树的节点个数(这个用于最后枚举以每个节点为根的子树满足条件后,求最大值用的)
void dfs(int u){ size[u]=1;//本身节点有1 if(son[u][0]!=-1){//判断有木有左鹅子 dfs(son[u][0]);//如果有递归左鹅子 size[u]+=size[son[u][0]];//当前节点size+=左鹅子节点size }//右鹅子同理 if(son[u][1]!=-1){ dfs(son[u][1]); size[u]+=size[son[u][1]]; } return; }
然后核心代码就是check了:
这里check是递归的check的;
当一个节点i既没有左儿子也没有右儿子,显然它是个叶子,那么它肯定对称,return 1;
当一个节点i既有左儿子又有右儿子,并且左右儿子权值相等时,我们递归的比较(左儿子的右儿子,右儿子的左儿子)比较(右儿子的右儿子,左儿子的左儿子),如果比到叶节点仍然相同,就可以认为以i为根的子树是轴对称的对称二叉树。其他只要有一点不满足,就一定不是对称二叉树。
bool check(int u,int v){ if(u==-1&&v==-1) return 1; if(u!=-1&&v!=-1&&val[u]==val[v]&&check(son[u][1],son[v][0])&&check(son[u][0],son[v][1])) return 1; return 0; }
最后上面写了吧↑
CODE:
#include<bits/stdc++.h> using namespace std; inline int read(){ int ans=0; char last=' ',ch=getchar(); while(ch<'0'||ch>'9') last=ch,ch=getchar(); while(ch>='0'&&ch<='9') ans=(ans<<1)+(ans<<3)+ch-'0',ch=getchar(); if(last=='-') ans=-ans; return ans; } int n; int val[1000005],son[1000005][2],size[1000005]; void dfs(int u){ size[u]=1; if(son[u][0]!=-1){ dfs(son[u][0]); size[u]+=size[son[u][0]]; } if(son[u][1]!=-1){ dfs(son[u][1]); size[u]+=size[son[u][1]]; } return; } bool check(int u,int v){ if(u==-1&&v==-1) return 1; if(u!=-1&&v!=-1&&val[u]==val[v]&&check(son[u][1],son[v][0])&&check(son[u][0],son[v][1])) return 1; return 0; } int main(){ memset(son,-1,sizeof(son)); n=read(); for(int i=1;i<=n;i++) val[i]=read(); for(int i=1;i<=n;i++){ son[i][0]=read(); son[i][1]=read(); } dfs(1); int ans=0; for(int i=1;i<=n;i++){ if(check(son[i][0],son[i][1])) ans=max(ans,size[i]); } cout<<ans<<endl; return 0; }
end-