人工智能基础
人工智能概述
历史
https://baike.baidu.com/item/人工智能/9180?fr=aladdin#9
人工智能、机器学习和深度学习
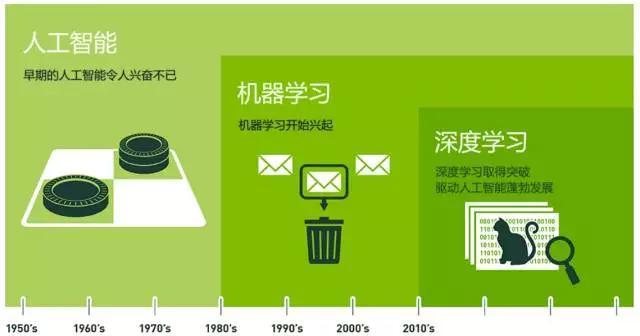
机器学习是人工智能的一个实现途径
深度学习是机器学习的一个方法发展而来
分支
- 计算机视觉:人脸识别
- 语言识别(难题:鸡尾酒会效应、声纹识别)
- 文本挖掘/分类
- 机器翻译
- 机器人
必备三要素
- 数据
- 算法
- 计算力
逐层、分布、并行算法能力提升
GPU、FPGA、TPU能力大幅提升
CPU和GPU
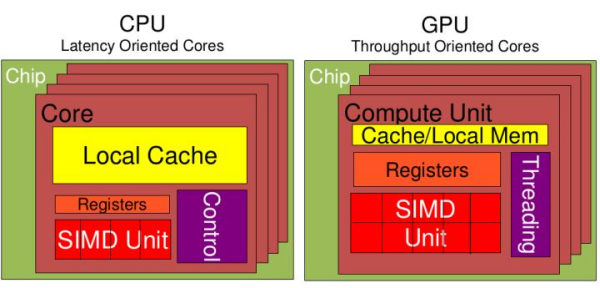
https://zhidao.baidu.com/question/422288800.html
- CPU -> IO密集型
- GPU -> 计算密集型
机器学习工作流程
定义
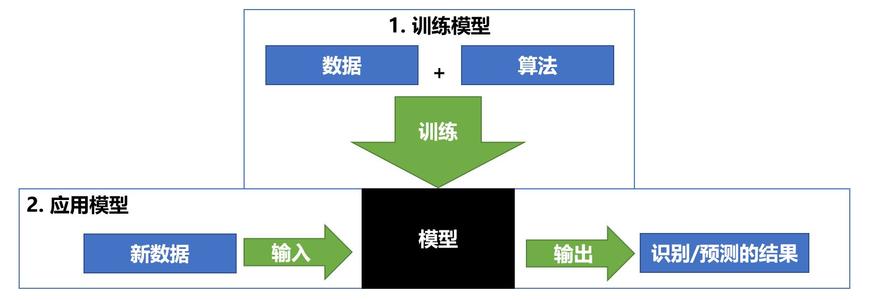
机器学习是从数据中自动分析获得模型,利用模型对未知数据进行预测
工作流程
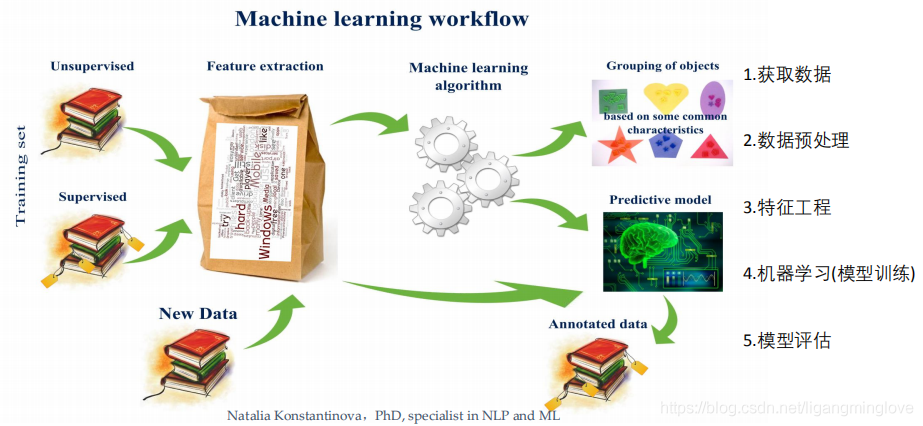
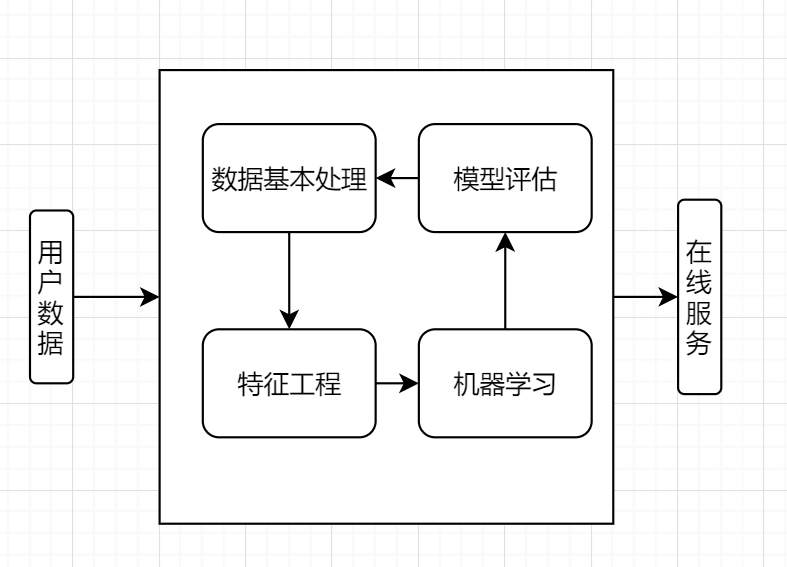
数据集
-
数据简介
在数据集中一般:
- 一行数据称为一个样本
- 一列数据称为一个特征
- 有些数据有目标值(标签值),有些数据没有目标值
-
数据类型构成:
- 特征值+目标值(目标值是连续的和离散的)
- 只有特征值,没有目标值
-
数据分割
- 机器学习一般的数据集会划分为两个部分:
- 训练数据:用于训练,构建模型
- 测试数据:在模型检验时使用,用于评估模型是否有效
- 划分比例:
- 训练集:70% 80% 75%
- 测试集:30% 20% 25%
- 机器学习一般的数据集会划分为两个部分:
数据基本处理
即对数进行缺失值、去除异常值等处理
特征工程
什么是特征工程
特征工程是使用专业背景知识和技巧处理数据,使得特征能在机器学习算法上发挥更好的作用的过程。
- 意义:会直接影响机器学习的效果
为什么需要特征工程
数据和特征决定了机器学习的上限,而模型和算法只是逼近这个上限而已
特征工程包含的内容
特征提取
将任意数据转换为可用于机器学习的数字特征
特征预处理
通过一些转换函数将特征数据转换成更适合算法模型的特征数据的过程
特征降维
在某些限定条件下,降低随机变量(特征)个数,得到一组“不相关”主变量的过程
机器学习算法分类
监督学习
- 定义:
- 输入数据是由输入特征值和目标值所组成
- 函数的输出可以是一个连续的值(称为回归)
- 或是输出有限个离散值(称作分类)
- 输入数据是由输入特征值和目标值所组成
回归问题
例如:预测房价,根据样本拟合出一条连续曲线
分类问题
例如:根据肿瘤特征判断是恶性还是良性,是离散的
无监督学习
-
定义:
-
输入数据是由输入特征值组成的
仅有特征值
-
半监督学习
-
定义:
有特征值,但是一部分数据有目标值,一部分没有
强化学习
实质是make decisions问题,即自动进行决策,并且可以做连续决策
主要包括:agent、环境状态、行动、奖励
例:
小孩要走路,但在这之前他需要先站起来,站起来之后还要保持平衡。接下来还要先迈出一条腿,是左腿还是右腿,迈出一步后还要迈出下一步。
小孩就是agent,他试图通过采取行动(即行走)来操纵环境(行走的表面),并且从一个状态转变到另一个状态(即他走的每一步),当他完成任务的子任务(即走了几步)时,他会得到奖励,并且当他不能走路时,就没有奖励
强化学习是动态过程,上一步数据的输出是下一步数据的输入,目的是获得最多的累计奖励
监督学习和强化学习的对比
| 监督学习 | 强化学习 | |
|---|---|---|
| 反馈映射 | 输入到输出的一个映射,监督式学习输出的是之间的关系,可以告诉算法什么样的输入对应什么样的输出 | 输入到输出的一个映射,强化学习输出的是给机器的反馈,即用来判断这个行为是好是坏 |
| 反馈时间 | 做了比较坏的选择会立刻反馈给算法 | 结果反馈有延时,有时候可能需要走了很多步以后才知道以前的某一步是好是坏 |
| 输入特征 | 输入是独立同分布的 | 面对的输入总是在变化,每当算法做出一个行为,它影响下一次决策的输入 |
| 行为模式 | 不考虑行为间的平衡,只是开发 | 一个agent可以在探索和开发中之间做权衡,并且选择一个最大的回报 |
模型评估
分类模型评估
- 准确率
- 预测正确数占样本总数的比例
- 精确率
- 正确预测为正占全部预测为正的比例
- 召回率
- 正确预测为正占全部正样本的比例
- F1-score
- 主要用于评估模型的稳健性
- AUC指标
- 主要用于评估样本不均衡的情况
回归模型评估
-
均方根误差
仅能比较误差是相同单位的模型
[RMSE = sqrt{frac{sum_{i=1}^{n}(p_i-a_i)^2}{n}} ]a = 实际目标
p = 预测目标
-
相对平方误差
可以比较误差是不同单位的模型
[RSE = frac{sum_{i=1}^n(p_i-a_i)^2}{sum_{i=1}^n(overline{a}-a_i)^2} ] -
平均绝对误差
与原始数据单位相同,仅能比较误差是相同单位的模型。量级近似与均方根误差,但是误差相对小一些
[MAE = frac{sum_{i=1}^nleftvert p_i-a_i ightvert}{n} ] -
相对绝对误差
可以比较误差是不同单位的模型
[RAE = frac{sum_{i=1}^nleftvert p_i-a_i ightvert}{sum_{i=1}^nleftvert overline{a}-a_i ightvert} ] -
决定系数
-
汇总解释度,由平方和术语计算而得
[R^2 = 1-frac{sum_{i=1}^n(p_i-a_i)^2}{sum_{i=1}^n(a_i-overline{a})^2} ] -
R2描述了回归模型所解释的因变量方差在总方差中的比例。R2很大,即自变量与因变量之间存在线性关系,如果回归模型是“完美的”,SSE为0,则R2为1。R2小,则自变量与因变量之间存在线性关系的证据不令人信服。如果回归模型完全失败,SSE等于SST,没有方差可被回归解释,则R^2为0
-
拟合

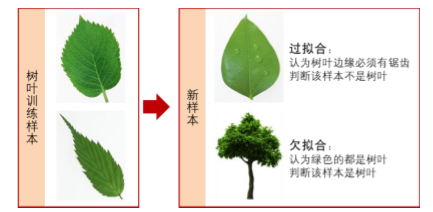
深度学习简介
神经网络简介
https://baike.baidu.com/item/人工神经网络/382460
深度学习演示:
http://playground.tensorflow.org/