格雷码Gray Code详解

格雷码简介

　　在一组数的编码中，若任意两个相邻的代码只有一位二进制数不同，则称这种编码为格雷码（Gray Code），另外由于最大数与最小数之间也仅一位数不同，即“首尾相连”，因此又称循环码或反射码。格雷码（Gray Code）又称Grey Code、葛莱码、格莱码、戈莱码、循环码、反射二进制码、最小差错码等。

格雷码有多种编码形式

十进制数	4位自然二进制码	4位典型格雷码	十进制余三格雷码	十进制空六格雷码	十进制跳六格雷码	步进码
0	0000	0000	0010	0000	0000	00000
1	0001	0001	0110	0001	0001	00001
2	0010	0011	0111	0011	0011	00011

...

表中典型格雷码具有代表性。若不作特别说明，格雷码就是指典型格雷码，它可从自然二进制码转换而来。

为什么要使用格雷码？

格雷码是一种具有反射特性和循环特性的单步自补码，其循环和单步特性消除了随机取数时出现重大错误的可能，其反射和自补特性使得对其进行求反操作也非常方便，所以，格雷码属于一种可靠性编码，是一种错误最小化的编码方式，因此格雷码在通信和测量技术中得到广泛应用。

格雷码属于可靠性编码，是一种错误最小化的编码方式。因为，虽然自然二进制码可以直接由数/模转换器转换成模拟信号，但在某些情况，例如从十进制的3转换为4时二进制码的每一位都要变，能使数字电路产生很大的尖峰电流脉冲。而格雷码则没有这一缺点，它在相邻位间转换时，只有一位产生变化。它大大地减少了由一个状态到下一个状态时逻辑的混淆。由于这种编码相邻的两个码组之间只有一位不同，因而在用于方向的转角位移量－数字量的转换中，当方向的转角位移量发生微小变化（而可能引起数字量发生变化时，格雷码仅改变一位，这样与其它编码同时改变两位或多位的情况相比更为可靠，即可减少出错的可能性。

在数字系统中，常要求代码按一定顺序变化。例如，按自然数递增计数，若采用8421码，则数0111变到1000时四位均要变化，而在实际电路中，4位的变化不可能绝对同时发生，则计数中可能出现短暂的其它代码（1100、1111等）。在特定情况下可能导致电路状态错误或输入错误。使用格雷码可以避免这种错误。

格雷码是一种绝对编码方式，典型格雷码是一种具有反射特性和循环特性的单步自补码，它的循环、单步特性消除了随机取数时出现重大误差的可能，它的反射、自补特性使得求反非常方便。

由于格雷码是一种变权码，每一位码没有固定的大小，很难直接进行比较大小和算术运算，也不能直接转换成液位信号，要经过一次码变换，变成自然二进制码，再由上位机读取。

典型格雷码是一种采用绝对编码方式的准权码，其权的绝对值为2^i-1(设最低位i=1)。

格雷码的十进制数奇偶性与其码字中1的个数的奇偶性相同。

应用

格雷氏编码与相位移在三维曲面量测：利用格雷码投射在微型曲面做量测 一个非接触式、投影的方法光学测量。

在化简逻辑函数时，可以通过按格雷码排列的卡诺图来完成。

角度传感器：汽车制动系统有时需要传感器产生的数字值来指示机械位置。如图是编码盘和一些触点的概念图，根据盘转的位置，触点产生一个3位二进制编码，共有8个这样的编码。盘中暗的区域与对应的逻辑1的信号源相连；亮的区域没有连接，触点将其解释为逻辑0。使用格雷码对编码盘上的亮暗区域编码，使得其连续的码字之间只有一个数位变化。这样就不会因为器件制造的精确度有限，而使得触点转到边界位置而出现错误编码。

九连环问题：中国的古老益智玩具九连环有着和格雷码完全相同的数学模式，外国一款名为spin out的玩具也是运用相同的数学模式。智力玩具九连环的状态 变化符合格雷码的编码规律，汉诺塔的解法也与格雷码有关。九连环中的每个环都有上下两种状态，如果把这两种状态用0/1来表示的话，这个状态序列就会形成一种循环二进制编码（格雷码）的序列。所以解决九连环问题所需要的状态变化数就是格雷码111111111所对应的十进制数341。

二进制格雷码的生成

问题：产生n位元的所有格雷码字符串表示。

　　格雷码(Gray Code)是一个数列集合，每个数使用二进位来表示，假设使用n位元来表示每个数字，任两个数之间只有一个位元值不同。

　　例如以下为3位元的格雷码： 000 001 011 010 110 111 101 100 。

　　如果要产生n位元的格雷码，那么格雷码的个数为2^n。

直接排列

生成二进制格雷码方式1：以二进制为0值的格雷码为第零项，第一项改变最右边的位元，第二项改变右起第一个为1的位元的左边位元，第三、四项方法同第一、二项，如此反复，即可排列出n个位元的格雷码。

假设原始的值从0开始，格雷码产生的规律是：

第一步，改变最右边的位元值；

第二步，改变右起第一个为1的位元的左边位元；

第三步，第四步重复第一步和第二步，直到所有的格雷码产生完毕（换句话说，已经走了(2^n) - 1 步）。

用一个例子来说明：

　　假设产生3位元的格雷码，原始值位 000

　　第一步：改变最右边的位元值： 001

　　第二步：改变右起第一个为1的位元的左边位元： 011

　　第三步：改变最右边的位元值： 010

　　第四步：改变右起第一个为1的位元的左边位元： 110

　　第五步：改变最右边的位元值： 111

　　第六步：改变右起第一个为1的位元的左边位元： 101

　　第七步：改变最右边的位元值： 100

镜射排列

生成二进制格雷码方式2：n位元的格雷码可以从n-1位元的格雷码以上下镜射后加上新位元的方式快速的得到，如图所示。

  

如果按照直接排列规则来生成格雷码，是没有问题的，但是这样做太复杂了。如果仔细观察格雷码的结构，我们会有以下发现：

　　1、除了最高位（左边第一位），格雷码的位元完全上下对称（看下面列表）。比如第一个格雷码与最后一个格雷码对称（除了第一位），第二个格雷码与倒数第二个对称，以此类推。

　　2、最小的重复单元是 0 , 1。

000
001
011
010
110
111
101
100

　　所以，在实现的时候，我们完全可以利用递归，在每一层前面加上0或者1，然后就可以列出所有的格雷码。

　　比如：

　　第一步：产生 0, 1 两个字符串。

　　第二步：在第一步的基础上，正向每一个字符串都分别加上0，然后反向迭代每一个字符串都加上1，但是每次只能加一个，所以得做两次。这样就变成了 00,01,11,10 （注意对称）。

　　第三步：在第二步的基础上，再给每个字符串都加上0和1，同样，每次只能加一个，这样就变成了 000,001,011,010,110,111,101,100。这样就把3位元格雷码生成好了。

　　如果要生成4位元格雷码，我们只需要在3位元格雷码上再加一层0,1就可以了： 0000,0001,0011,0010,0110,0111,0101,0100,1100,1101,1110,1010,0111,1001,1000.

 　　也就是说，n位元格雷码是基于n-1位元格雷码产生的。
[格雷码维基百科]
其它方法

利用卡诺图生成

利用卡诺图相邻两格只有一位变化以及卡诺图的变量取值以低阶格雷码的顺序排布的特征，可以递归得到高阶格雷码。由于此方法相对繁琐，使用较少。生成格雷码的步骤如下：

1. 将卡诺图变量分为两组，变量数目相近（最好相等）
2. 以逻辑变量高位在左低位在右建立卡诺图
3. 从卡诺图的左上角以之字形到右上角最后到左下角遍历卡诺图，依次经过格子的变量取值即为典型格雷码的顺序

[百度百科 格雷码]

利用二进制码转换

转换方法参考下面吧。

格雷码和二进制码的转换

自然二进制码与格雷码的对照表：   

十进制数	自然二进制数	格雷码	十进制数	自然二进制数	格雷码
0	0000	0000	8	1000	1100
1	0001	0001	9	1001	1101
2	0010	0011	10	1010	1111
3	0011	0010	11	1011	1110
4	0100	0110	12	1100	1010
5	0101	0111	13	1101	1011
6	0110	0101	14	1110	1001
7	0111	0100	15	1111	1000

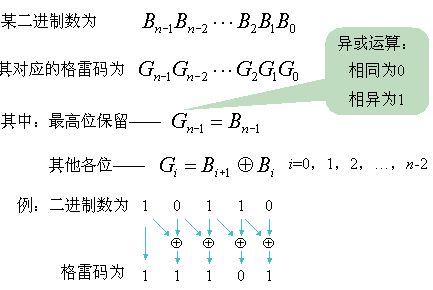
二进制码转换成二进制格雷码

　　二进制码转换成二进制格雷码，其法则是保留二进制码的最高位作为格雷码的最高位，而次高位格雷码为二进制码的高位与次高位相异或，而格雷码其余各位与次高位的求法相类似。 

二进制码 ----> 格雷码(编码)：从最右边一位起，依次将每一位与左边一位异或(XOR)，作为对应格雷码该位的值，最左边一位不变(相当于左边是0)。

Note: 这样做可行的原因，是因为二进制码每次+1时最多只有一个相邻的两个bit对的异或值会发生改变。

公式表示：G：格雷码 B：二进制码
整个数G(N) = (B(n) >> 1) XOR B(n)

单个位

 

　　

格雷码转换成二进制码

二进制格雷码转换成二进制码，其法则是保留格雷码的最高位作为自然二进制码的最高位，而次高位自然二进制码为高位自然二进制码与次高位格雷码相异或，而自然二进制码的其余各位与次高位自然二进制码的求法相类似。 

公式表示：

 

格雷码转换为二进制码算法有以下几种表述形式：

表述一：

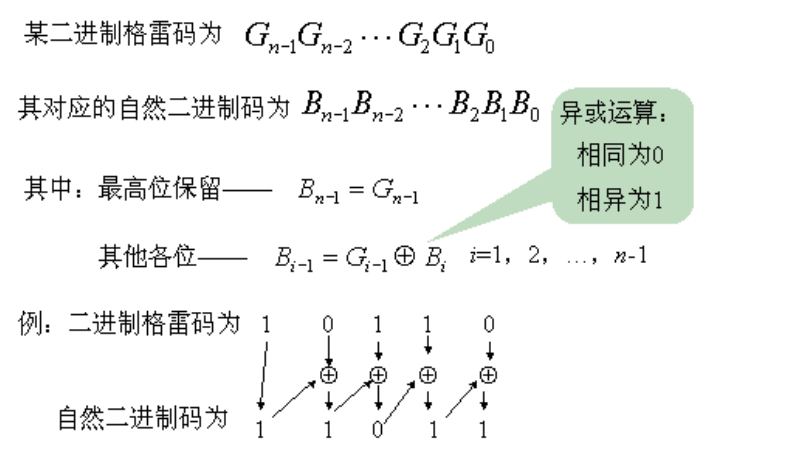
    二进制格雷码为Gn-1Gn-2...G2G1G0

    自然二进制码为Bn -1Bn-2...B2B1B0

    其中：最高位保留  Bn-1=Gn-1

    其他各位  Bi-1=Gi-1 xor Bi ，i=1,2,...,n-1

表述二：

    Bi = ˆG[n-1:i]=G[n-1]ˆG[n-2]ˆ..ˆG[i]，i=0,1,...,n-1

表述三：

    Bi = ˆ(G>>i)，i=0,1,...,n-1

[格雷码（Gray Code）转二进制码（Binary Code）]

[格雷码与二进制的转换]

皮皮blog

二进制格雷码字符串生成

c++ stl递归和非递归代码

vector<string> gray0(int n) {
    /*
     * 格雷码字符串的直接排列递归实现
     * 思路:1、获得n-1位生成格雷码的数组
     *      2、由于n位生成的格雷码位数是n-1的两倍，故只要在n为格雷码的前半部分加0，后半部分加1即可。
     */
    if (n == 0)
        return vector<string>{"0"};
    else if (n == 1) {
        return vector<string>({"0", "1"});
    } else {
        vector<string> new_gray_code;
        vector<string> gray_code = gray0(n - 1);
//        vector<string> gray_code = vector<string>({"0", "1"});

        vector<string>::iterator gc_it;
        for (gc_it = gray_code.begin(); gc_it != gray_code.end(); gc_it++)
            new_gray_code.push_back("0" + *gc_it);

        vector<string>::reverse_iterator gc_rit;
        for (gc_rit = gray_code.rbegin(); gc_rit != gray_code.rend(); gc_rit++)
            new_gray_code.push_back("1" + *gc_rit);
        return new_gray_code;
    }
}


vector<string> gray1(int n) {
    /*
     * 格雷码字符串的镜射排列非递归实现
     */
    if (n == 0)
        return vector<string>{"0"};

    vector<string> gray_code = vector<string>({"0", "1"});
    while (--n) {
        vector<string> new_gray_code;

        vector<string>::iterator gc_it;
        for (gc_it = gray_code.begin(); gc_it != gray_code.end(); gc_it++)
            new_gray_code.push_back("0" + *gc_it);

        vector<string>::reverse_iterator gc_rit;
        for (gc_rit = gray_code.rbegin(); gc_rit != gray_code.rend(); gc_rit++)
            new_gray_code.push_back("1" + *gc_rit);

        gray_code = new_gray_code;
    }
    return gray_code;
}

非stl c++代码[格雷码那点事——递归非递归实现][格雷码的实现]

格雷码还有一种实现方式是根据这个公式来的 G(n) =  B(n) XOR B(n+1), 这也是格雷码和二进制码的转换公式。代码如下：

    public void getGrayCode(int bitNum){  
        for(int i = 0; i < (int)Math.pow(2, bitNum); i++){  
            int grayCode = (i >> 1) ^ i;  
            System.out.println(num2Binary(grayCode, bitNum));  
        }  
    }  
    public String num2Binary(int num, int bitNum){  
        String ret = "";  
        for(int i = bitNum-1; i >= 0; i--){  
            ret += (num >> i) & 1;  
        }  
        return ret;  

    }