编程题(四)
问题描述
小明有一块空地,他将这块空地划分为 (n) 行 (m) 列的小块,每行和每列的长度都为 (1) 。
小明选了其中的一些小块空地,种上了草,其他小块仍然保持是空地。
这些草长得很快,每个月,草都会向外长出一些,如果一个小块种了草,则它将向自己的上、下、左、右四小块空地扩展,这四小块空地都将变为有草的小块。
请告诉小明,(k) 个月后空地上哪些地方有草。
输入格式
输入的第一行包含两个整数 (n) , (m) 。
接下来 (n) 行,每行包含 (m) 个字母,表示初始的空地状态,字母之间没有空格。如果为小数点,表示为空地,如果字母为 (g),表示种了草。
接下来包含一个整数 (k)。
输出格式
输出 (n) 行,每行包含 (m) 个字母,表示 (k) 个月后空地的状态。如果为小数点,表示为空地,如果字母为 (g),表示长了草。
评测用例规模与约定
对于 (30\%) 的评测用例,(2 <= n, m <= 20)。
对于 (70\%) 的评测用例,(2 <= n, m <= 100)。
对于所有评测用例,(2 <= n, m <= 1000),(1 <= k <= 1000)。
——————————————————————————————
也是直接模拟草的生长情况就好了。
由于同一位置下长草时间更早的情况覆盖了更晚的,所以我们只需考虑一块地最先长草的状态。
我们可以使用队列来优化掉冗余的状态,时间复杂度 (O(n*m)) 。
(way) 数组控制方向,(f) 数组标记一块地是否长过草,(dt) 数组实时更新地图情况。
代码如下:
#include <bits/stdc++.h>
#define MAXN 1007
using namespace std;
struct Point { int x,y,c; };
int n,m,k,way[4][2]={{1,0},{-1,0},{0,1},{0,-1}};
char dt[MAXN][MAXN]; bool f[MAXN][MAXN];
queue<Point> Q;
int main() {
memset(f,0,sizeof(f));
scanf("%d%d",&n,&m);
for (int i=0;i<n;i++) {
scanf("%s",dt[i]);
for (int j=0;j<m;j++)
if (dt[i][j]=='g')
f[i][j]=true,Q.push((Point){i,j,0});
}
scanf("%d",&k);
while(!Q.empty()) {
Point now=Q.front(); Q.pop();
if (now.c==k) break;
for (int i=0;i<4;i++) {
int tx=now.x+way[i][0],ty=now.y+way[i][1];
if (tx<0 || tx>n || ty<0 || ty>m) continue;
dt[tx][ty]='g';
if (!f[tx][ty]) Q.push((Point){tx,ty,now.c+1});
}
}
for (int i=0;i<n;i++) printf("%s
",dt[i]);
return 0;
}
##编程题(五)
问题描述
小明想知道,满足以下条件的正整数序列的数量:
- 第一项为 (n) ;
- 第二项不超过 (n) ;
- 从第三项开始,每一项小于前两项的差的绝对值。
请计算,对于给定的 (n) ,有多少种满足条件的序列。
输入格式
输入一行包含一个整数 (n) 。
输出格式
输出一个整数,表示答案。答案可能很大,请输出答案除以 (10000) 的余数。
评测用例规模与约定
对于 (20\%) 的评测用例,(1 <= n <= 5)。
对于 (50\%) 的评测用例,(1 <= n <= 10)。
对于 (80\%) 的评测用例,(1 <= n <= 100)。
对于所有评测用例,(1 <= n <= 1000)。
——————————————————————————————
(50) 分的做法就是直接暴力 (dfs),首先敲了如下代码,再进行优化。
#include <bits/stdc++.h>
#define MAXN 1007
using namespace std;
int ans,a[100007];
int dfs(int st) {
ans++;
int cha=abs(a[st]-a[st-1]);
for (int i=1;i<cha;i++) {
a[st+1]=i,dfs(st+1);
}
}
int main() {
int n;
scanf("%d",&n),a[1]=n;
for (int i=1;i<=n;i++) {
a[2]=i,dfs(2);
}
printf("%d",ans);
return 0;
}
发现题干一直在强调前两项的差值,于是意识到后一项的值与其密切相关。
由于有了绝对值和正数这两个限制,前两项具体的值都也存在影响。
用上面的程序打表观察一下,发现连续两项的相同的后继项完全一致,这里可以做一个记忆化处理。
经过剪枝的 (dfs) 就大概可以通过 (80\%) 的数据了。
正解应该是 (DP),常数比搜索小一些,但我这里直接打表过了。
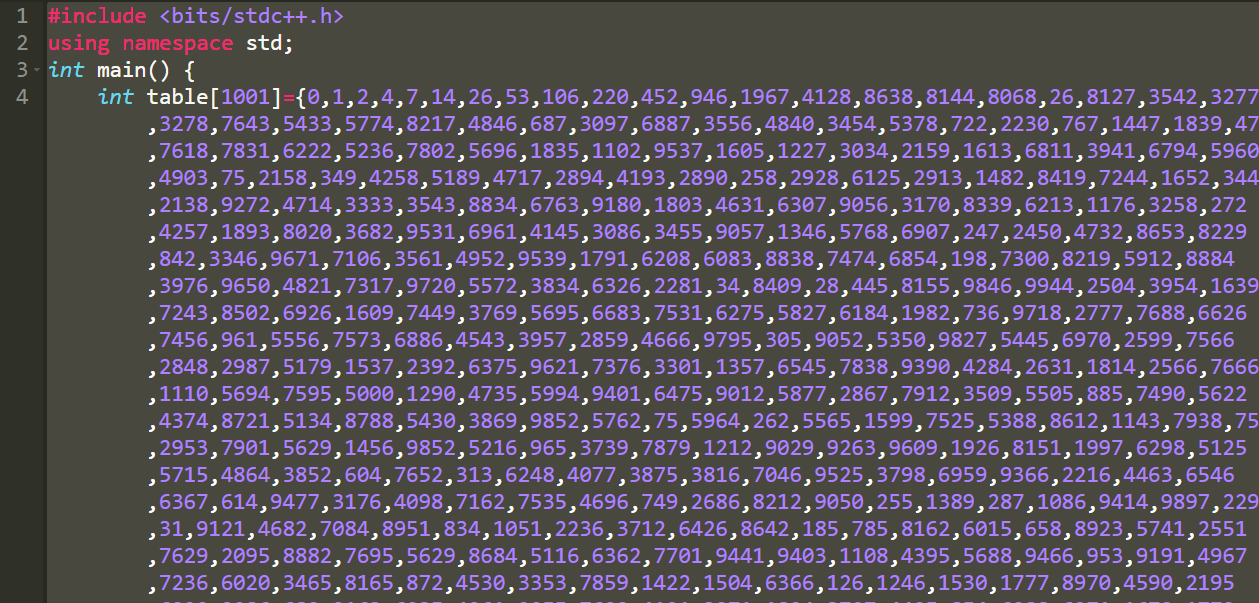
制表代码如下:
#include <bits/stdc++.h>
#define MAXN 1007
#define mod 10000
using namespace std;
int ans,f[MAXN][MAXN];
int dfs(int p1,int p2) {
if (f[p1][p2]) return f[p1][p2];
f[p1][p2]=1;
for (int i=1;i<abs(p1-p2);i++)
f[p1][p2]+=dfs(p2,i),f[p1][p2]%=mod;
return f[p1][p2];
}
int main() {
freopen("","w",stdout);
printf("int table[1001]={0,");
for (int n=1;n<=1000;n++) {
ans=0;
for (int i=1;i<=n;i++)
ans+=dfs(n,i),ans%=mod;
printf("%d",ans);
if (n!=1000) printf(",");
}
printf("}");
return 0;
}
##编程题(六)
问题描述
小明要组织一台晚会,总共准备了 (n) 个节目。然后晚会的时间有限,他只能最终选择其中的 (m) 个节目。
这 (n) 个节目是按照小明设想的顺序给定的,顺序不能改变。
小明发现,观众对于晚上的喜欢程度与前几个节目的好看程度有非常大的关系,他希望选出的第一个节目尽可能好看,在此前提下希望第二个节目尽可能好看,依次类推。
小明给每个节目定义了一个好看值,请你帮助小明选择出 (m) 个节目,满足他的要求。
输入格式
输入的第一行包含两个整数 (n) , (m) ,表示节目的数量和要选择的数量。
第二行包含 (n) 个整数,依次为每个节目的好看值。
输出格式
输出一行包含 (m) 个整数,为选出的节目的好看值。
评测用例规模与约定
对于 (30\%) 的评测用例,(1 <= n <= 20);
对于 (60\%) 的评测用例,(1 <= n <= 100);
对于所有评测用例,(1 <= n <= 100000),(0 <= value <= 100000)。
——————————————————————————————
一个贪心题。
由于在小明的策略下一定是要选择当前能选中好看值最大的节目,所以每次选择就是在当前能选的节目中找好看值最大的,不考虑之后如何选择。
当然小明至少要给未选节目们留最小的选择空间,不然就无法选够 (m) 个节目,
于是发现当前能选的节目是一个区间,比如小明还有 (p) 个节目要选,共 (n) 个节目,上次选了 (k) 号节目。
那么他的本次选择节目区间就是 ([k+1,n-p+1]),如此迭代,就可以确定每次的选择。
对于 (60) 分来说每次在区间内容找最大值即可,优化的话就是加入记录了最大值和最大值来源 (ST) 表(我们同时关心这两个值)。
还要注意如果区间上有多个值相等,应该保留位置靠前的一个(贪心)。
代码如下:
#include <bits/stdc++.h>
#define MAXN 100007
using namespace std;
struct Seg { int val,id; }st[MAXN][20];
int n,m,k,v[MAXN];
inline void init() {
for (int j=1;j<=log2(n);j++)
for (int i=1;i<=n-(1<<j)+1;i++) {
if (st[i][j-1].val<st[i+(1<<(j-1))][j-1].val)
st[i][j]=st[i+(1<<(j-1))][j-1];
else st[i][j]=st[i][j-1];
}
}
inline Seg q(int l,int r) {
int t=log2(r-l+1);
if (st[l][t].val>=st[r-(1<<t)+1][t].val) return st[l][t];
else return st[r-(1<<t)+1][t];
}
int main() {
scanf("%d%d",&n,&m);
for (int i=1;i<=n;i++) scanf("%d",&st[i][0].val),st[i][0].id=i;
init(),k=1;
for (int i=m;i>=1;i--) {
Seg now=q(k,n-i+1);
k=now.id+1,printf("%d ",now.val);
}
return 0;
}