预备知识
二进制,十六进制,二进制与十进制的转化运算
根据冯诺依曼结构的运算器,只有加法运算器,没有减法运算器
所以,计算机中不是直接做减法,是通过加法来实现的。所以就必须引入一个符号位
原码,反码,补码 的产生就是为了解决这个问题
原码
最简单的机器数表示法
原码:
最高位表示符号位,1表示负,0表示正
其他位存放该数的二进制的绝对值
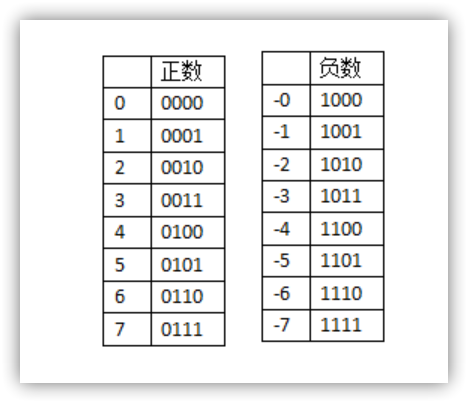
直接用原码运算
0001+0010=0011 (1+2=3)正确
0000+1000=1000 ((+0)+(-0)=-0)
0001+1001=1010 (1+(-1)=-2)出错
1001+1001= ?
原码正数之间的加法通常不会出错
正数与负数相加,或负数与负数相加,问题就出现了
所以,原码直观易懂,易于正值转换,但用来实现加减法的话,运算规则总归是太复杂,于是反码来了
反码
原码最大的问题就在于一个数加上他的相反数不等于零,反码的设计思想就是为了解决这一点
反码:
正数的反码=原码
负数的反码=原码除符号位外,按位取反
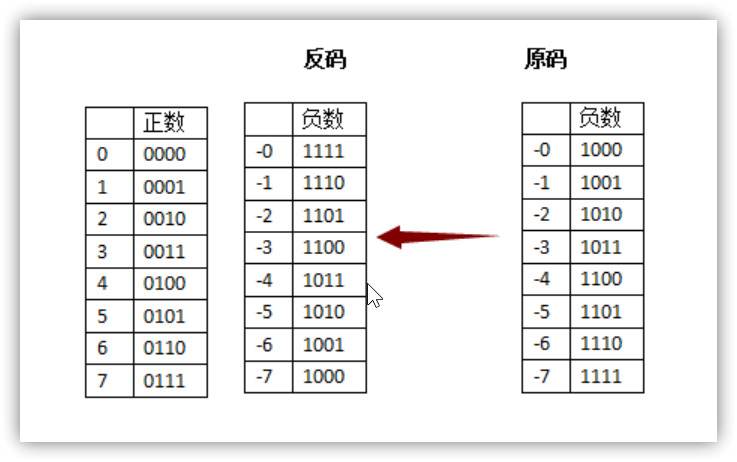
我们试着用反码运算
0001+1110=1111 (1+(-1)=(-0)) 有点问题,也正确
1110+1101=1011 (-1)+(-2)=(-4) 两个负数相加,出错
负数相加出错,问题不大,我们只需要在两个负数相加时,将两个负数反码包括符号位全部按位取反相加,然后再给他的符号位强置‘1’就可以了。
反码表示法其实已经解决了减法的问题,他不仅不会像原码那样出现两个相反数相加不为零的情况,而且对于任意的一个正数加负数,计算结果是正确的
然后就有了补码
补码
补码:
正数的补码=原码
负数的补码=反码+1
负数的补码的另外一种算法:
自低位向高位,尾数第一个1及其右部的0保持不变,左部取反,符号位不变
其实上面两段话,都只是补码的求法,而不是补码的定义,基础工作者并不会心血来潮的把反码+1就定义为补码,只不过是补码正好就等于反码加1罢了
暂时先忘记书上那句负数的补码等于它的反码+1,我们的理解陷入了误区
这也是为什么《计算机组成原理》要特意先讲补码,再讲反码
接下来我们要重点讲讲补码的思想
补码的思想
为了理解,先得引入模和同余的思想
模 其实就是一个计量器的容量大小,比如钟表的模M=12
同余 是指两个整数A和B除以同一个正整数M,所得余数相同,比如1点和13点,2点和14点就是同余的,可以写作
1 = 13 mod (12), 2 = 14 mod (12)
如果说现在时针现在停在10点钟,那么什么时候时针会停在8点钟呢?
这么说吧,因为过去2个小时前是8点,所以未来10个小时候也是8点
也就是说:倒拨2小时 或 正拨10小时 都是八点钟
10-2=8,(10+10)mod(12)=8
所以,10-2和10+10从另一个角度来看是等效的,它都使时针指向了8点钟
既然是等效的,那在时钟运算中,减去一个数,其实就相当于加上另外一个数(这个数与减数相加正好等于12,也就是同余数)
我再次强调,原码,反码,补码的引入是为了解决做减法的问题。在原码,反码表示法中,我们把减法化为加法的思维是减去一个数,等于加上一个数的相反数,结果由于引入符号位造成了各种问题
那你应该知道我要说什么了,利用模和同余的概念,我们可以使减法运算转化为加法运算
而现在,我们不引入负数的概念,就可以把减法当成加法来算
所以接下来我们聊4位二进制数的运算,也不必急于引入符号位。因为补码的思想,把减法当成加法时并不是必须要引入符号位的。
而且我们可以通过下面的例子,也许能回答另一个问题,为什么负数的符号位是‘1’,而不是正数的符号位是‘1’
四位二进制补码运算实例
0110 - 0010 (6-2=4) 计算机中没有减法器,不能直接算
但是现在你知道,减去一个数,可以等同于加上另外一个正数(同余数)
那么这个数是什么呢?时钟运算中我们可以看出这个数与减数相加正好等于模M=12
四位二进制数的模(计量器)=四位二进制数最大容量=2^4=16=10000B
那么2(0010)的同余数,就等于10000-0010=1110(14)
既然如此
0110(6) - 0010(2) = 0110(6) + 1110(14) = 10100(16+4=20)
OK,我们看到按照这种算法得出的结果是10100,但是对于四位二进制数,最大只能存放4位(硬件决定),正好是0100(4),就是我们想要的结果,至于最高位的 1,计算机会把他放入psw寄存器进位位中。8位机则会放在cy中,x86会放在cf中(不作讨论)
这个时候,我们再想想在四位二进制数中,减去2,就相当于加上它的同余数14
但是减去2,从另外一个角度来说,也是加上(-2)。即加上(-2)和加上14其实得到的二进制结果除了进位位,结果是一样的。
如果我们把1110(14)的最高位看作符号位后就是(-2)的补码,这可能也是为什么负数的符号位是‘1’而不是‘0’,
而且在有符号位的四位二进制数中,能表示的只有‘-8~7’,而无符号位数(14)的作用和有符号数(-2)的作用效果其实是一样的。
那正数的补码呢?加上一个正数,加法器就直接可以实现。所以它的补码就还是它本身。
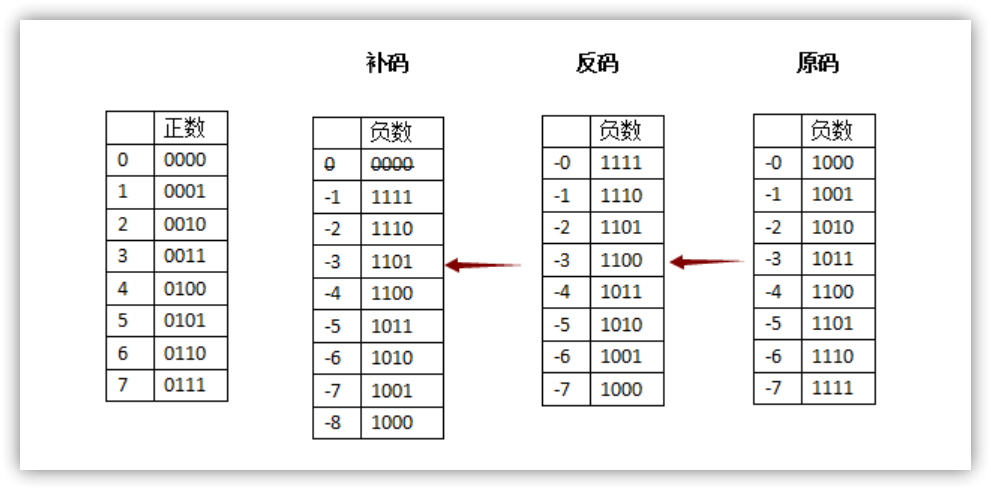
到这里,我们发现原码,反码的问题,补码基本解决了。
做减法时,0001(1)+1111(-1)=0000,我们再也不需要一个1000来表示负0了,就把1000规定为-8
负数与负数相加的问题也解决了1111(-1)+1110(-2)=1101(-3)
为什么可以+1
然后我们再来看看为什么负数的补码的求法为什么是反码+1
因为负数的反码加上这个负数的绝对值正好等于1111,再加1,就是1000,也就是四位二进数的模
而负数的补码是它的绝对值的同余数,可以通过模减去负数的绝对值,得到他的补码。
所以,负数的补码就是它的反码+1
算补码的小技巧
如果我们把-8当成负数的原点。那么-5的补码是多少呢?
-5 = -8 + 3
-5的补码就是-8的补码加3
1000(-8) + 0011(3) = 1011(-5)
也可以记住-1的补码是1111口算减法得出
1111(-1) - 0100(4) = 1011(-5)
对于八位加法器的话,可以把-128当补码原点。十六位可以把-32768当补码原点。
是的,128是256(八位二进制数的模)的一半,32768是65536(十六位二进数的模)的一半
也很方便有没有,而且简单的是
补码原点总是最高位是‘1’,其他位是‘0’
感谢阅读