计算几何导论

计算几何

计算几何是一门兴起于二十世纪七十年代末的计算机科学的一个分支，主要研究解决几何问题的算法。在现代工程和数学领域，计算几何在图形学、机器人技术、超大规模集成电路设计和统计等诸多领域有着十分重要的应用。

计算几何问题的输入一般是关于一组几何对象的描述，如一组点、一组线段，或者一个多边形的按逆时针顺序排列的一组顶点。输出常常是对有关这些对象的问题的回答，如是否直线相交，是否为一个新的几何对象，如顶点集合的凸包。

本文将介绍一些平面上的计算几何算法。在这些算法中，每个输入对象都是一组点{p1,p2,p3...}，其中每个pi=(xi,yi)。

点与向量

向量也称为矢量，是一种既有大小又有方向的量。在计算几何中，某个向量从点A指向点B，记为向量AB。

二维直角坐标系中的向量可以沿坐标轴分解，向量AB=xi+yj。所以向量AB可以用实数(x,y)来表示，同理n维向量也可以用n个实数来表示。因此一个点也可以表示一个向量。

向量的基本运算包括加减法，数乘，点积，叉积，混合积等。

如果有向量a=(x1,y1)，向量b=(x2,y2)。那么：

1. 向量a的长度|a|=sqrt(x²+y²)。
2. 加法的定义为：向量a+向量b=(x1+x2,y1+y2)。减法同理。
3. 数乘是向量和实数之间的运算，如果是一个正实数与向量相乘，向量只发生大小变化，方向不变。乘以负数则会将原向量反向，乘以0则变成零向量。
4. 点积，也叫数量积或内积，得到的结果是一个实数。定义向量a·向量b=x1y1+x2y2。点积满足交换律不满足结合律。
5. 叉积，也叫矢量积或外积。定义向量aX向量b=x1y2-x2y1，即两个向量形成的平行四边行的面积。

因为计算几何中经常涉及精度问题，需要对一个很小的数判断正负，为了修正误差，需要引入一个极小量eps。

const double eps=1e-8;
int dcmp(double x){
    if (fabs(x)<eps) return 0;
    if (x>0) return 1;
    return -1;
}

我们设计一个二维点类，使它可以进行一些常见的向量运算。点类也是其它计算几何问题的基础。

const double pi=acos(-1.0);
inline double sqr(double x){return x*x;}// 平方
struct Point{
    double x,y;
    Point(){}
    Point(double a,double b):x(a),y(b){}// 构造
    void input(){scanf("%lf%lf",&x,&y);}// 读入
    double norm(){return sqrt(sqr(x)+sqr(y));}// 到原点的距离
    /** 运算 **/
    friend Point operator+(const Point &a,const Point &b){
        return Point(a.x+b.x,a.y+b.y);
    }
    friend Point operator-(const Point &a,const Point &b){
        return Point(a.x-b.x,a.y-b.y);
    }
    friend bool operator==(const Point &a,const Point &b){
        return dcmp(a.x-b.x)==0&&dcmp(a.y-b.y)==0;
    }
    friend Point operator*(const Point &a,const double &b){
        return Point(a.x*b,a.y*b);
    }
    friend Point operator*(const double &a,const Point &b){
        return Point(a*b.x,a*b.y);
    }
    friend Point operator/(const Point &a,const double &b){
        return Point(a.x/b,a.y/b);
    }
};
double det(const Point &a,const Point &b){return a.x*b.y-a.y*b.x;}// 叉乘
double dot(const Point &a,const Point &b){return a.x*b.x+a.y*b.y;}// 点乘
double dist(const Point &a,const Point &b){return (a-b).norm();}// 距离

线段的性质

线段

我们称p1和p2为线段p₁p₂的端点。如果要考虑p1和p2之间的顺序，称线段为有向线段。如果有向线段p₁p₂的起点p1是坐标原点(0,0)，则可以称其为向量p2。

实现一个线段类，用有向线段上的两个端点a->b来表示一个线段。

struct Line{
    Point a,b;
    Line(){}
    Line(Point x,Point y):a(x),b(y){}
};

叉积

叉积是线段相关算法的中心。考虑图示两个向量p1和p2。

可以把叉积p1Xp2看作是由点(0,0),p1,p2和p1+p2=(x1+x2,y1+y2)所形成的平行四边形的面积。也可以把叉积定义为一个矩阵的行列式。

p1Xp2=x1y2-x2y1=-p2Xp1

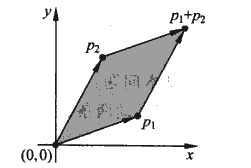
如果p1Xp2为正数，则相对于原点(0,0)来说，p1在p2的顺时针方向上；如果p1Xp2为负数，则p1在p2的逆时针方向上。

如果叉积为0的话，说明这两个向量是共线的，它们指向相同的方向或相反的方向。

如果公共端点不是原点而是p0，判断有向线段p₀p₁在有向线段p₀p₂的顺时针方向还是逆时针方向，只需定义p1'=p1-p0，p2'=p2-p0。

然后计算叉积p1'Xp2'=(p1-p0)X(p2-p0)=(x1-x0)(y2-y0)-(x2-x0)(y1-y0)

如果该叉积为正，则有向线段p₀p₁在有向线段p₀p₂的顺时针方向；叉积为负，在逆时针方向；叉积为0，它们共线。

折线的拐角方向判断

对于两条连续的有向线段p₀p₁和p₁p₂，我们可以判断它们在点p1处是左转还是右转。

如图所示，只需检查有向线段p₀p₂是在有向线段p₀p₁的顺时针方向还是逆时针方向即可。

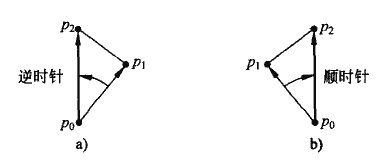
计算叉积(p2-p0)X(p1-p0)，如果为负，则在p1左转；如果为正，在p1右转；如果为0，不转向是直线。

线段相交 

如果一个线段的两个端点在一条直线的两边，我们称这条线段跨越了这条直线。

两个线段相交，当且仅当下面两个条件中至少一个成立：

1. 一个线段的某一个端点在另一条线段上。
2. 每个线段都跨越另一条线段所在的直线。

下面的代码实现了这一思想。

如果线段规范相交返回2，非规范相交返回1，不相交返回0。

过程Direction，利用叉积计算出线段的相对方位。过程OnSegment，用于确定一个与某一线段共线的点是否位于线段上。

double Direction(Point pi,Point pj,Point pk){
    return det(pk-pi,pj-pi);
}
bool OnSegment(Point pi,Point pj,Point pk){
    if (min(pi.x,pj.x)<=pk.x&&pk.x<=max(pi.x,pj.x)&&min(pi.y,pj.y)<=pk.y&&pk.y<=max(pi.y,pj.y)) return true;
    return false;
}
int SegCrossSeg(Line u,Line v){
    Point p1=u.a,p2=u.b,p3=v.a,p4=v.b;
    int d1=dcmp(Direction(p3,p4,p1));
    int d2=dcmp(Direction(p3,p4,p2));
    int d3=dcmp(Direction(p1,p2,p3));
    int d4=dcmp(Direction(p1,p2,p4));
    if ((d1^d2)==-2&&(d3^d4)==-2) return 2;
    if ((d1==0&&OnSegment(p3,p4,p1))||
        (d2==0&&OnSegment(p3,p4,p2))||
        (d3==0&&OnSegment(p1,p2,p3))||
        (d4==0&&OnSegment(p1,p2,p4))) return 1;
    return 0;
}

处理流程：计算出每个端点pi相对于另一线段的相对方位di。如果所有的方位都非0，则可以容易的确定线段是否规范相交，1^-1=-2，如果d1与d2或d3与d3符号不同的话，它们的异或值就是-2。否则我们判断端点与线段共线的情况中是否有边界情况，如果某点在另一条线段上，则它们不规范相交。其它情况则不相交。

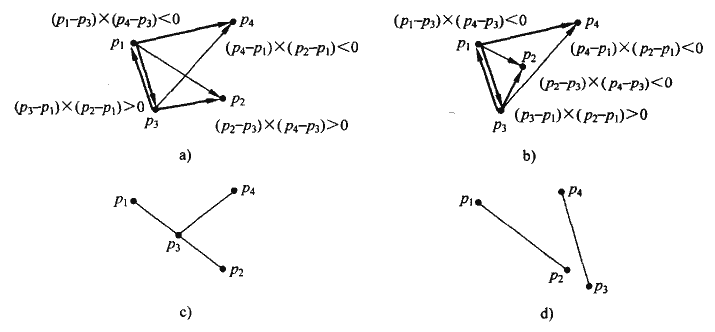
线段求交问题

基本概念

给定平面上n条线段，判断其中是否有两条线段相交。

容易想到枚举每两条线段，判断它们是否相交，复杂度O(n²)。这里介绍一种利用扫描线的O(nlogn)的算法。

算法描述

扫描算法在许多计算几何算法中都用到了。

扫描线是一个假想的垂直的线，它从左到右移动。

为了简化问题，我们先假设输入中没有一条线段是垂直的，没有三条线段共线。最后对算法稍作改动，使假设不成立时仍能正常工作。

排序线段

因为假定不存在垂直线段，所以任何与给定垂直扫描线相交的输入线段与其有一个交点。根据交点的y坐标对交点进行排序。

对于两条线段s1和s2。如果一条横坐标为x的垂直扫描线与这两条线段都相交，则说这两条线段在x是可比的。如果s1和s2在x处是可比的，并且在x处，s1与扫描线的交点比s2与扫描线的交点高，则说x处s1位于s2之上，写作s1>r^s2。

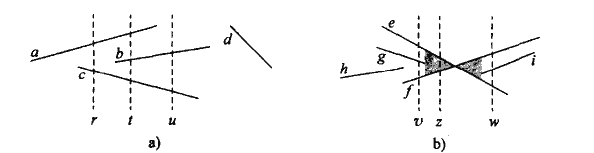
如图a>r^c，a>t^b，b>t^c，a>t^c，b>u^c，线段d与其他任何线段都不可比。

当扫描线穿过两条线段的交点时，如图，它们在扫描线中的顺序颠倒了，扫描线v和w分别位于线段e和f的交点的左边和右边，有e>v^f，f>w^e。

注意我们假定没有三条线段相交于同一点，所以必有某条垂直扫描线x，使得相交线段e和f在扫描线中时连续的。任何穿过图中阴影区域的扫描线，e与f都在其中连续。

扫描线的移动

典型的扫描算法要维护下列两组数据。

扫描线状态：与扫描线相交的物体之间的关系

事件点调度：从左向右排列的x坐标的序列，它定义了扫描线的暂停位置。称每个这样的暂停位置为事件点。扫描线状态仅在事件点处才会发生变化。

对于某些算法，事件点调度是随算法执行而动态确定的。我们现在讨论的仅仅是基于输入数据的简单性质静态的确定事件点，这里每条线段的端点都是事件点。

我们通过x坐标，从左向右对线段的端点进行排序。如果有两个或更多端点位于同一条垂直线上，即有相同的x坐标，就将所有的左端点放置在右端点之前。对于x坐标相同的左端点们，将y坐标小的放置在前面，右端点也是如此。

在扫描过程中，当遇到左端点时，就把改线段插入到扫描线状态中，并且当遇到其右端点时，就把它从扫描线状态中删除。每当两条线段在扫描线中第一次变为连续时，就检查它们是否相交。

因此在扫描中有以下操作：

• 把线段s插入到扫描线中。
• 把线段s从扫描线中删除。
• 返回紧邻线段s的上下两条线段。

可以用各种平衡二叉树用O(logn)的复杂度来维护这些操作。在树上用叉积来比较两条线段的相对顺序。

具体流程

1. 将所有线段的端点加入事件队列Q。
2. 设S为所有和扫描线L相交的线段集合，初始S为空。
3. 从Q中取出下一个横坐标x最小的端点E。
4. 如果E是一条线段b的左端点，将此线段加入S中，接着找出S中与b上下相邻的两条线段a和c，检查是否(a,b)或(b,c)相交。
5. 如果E是一条线段b的右端点，从S中找出b上下相邻的两条线段a和c，将b从S中删去，同时判断(a,c)是否相交。
6. 如果Q中还有事件，返回第3步，否则算法结束。

点的有序化

基本概念

在处理一些问题时，需要对一个无序的点集进行排序，通常情况下要使得排序后的有序点集组成一个简单多边形。

有两种算法可以实现，极角排序和水平排序。

极角排序

极角排序一般选一个点作为极点，从这个极点张开一个极角坐标系，其余点在这个极坐标系中的角度值称为该点的极角。

将非极点按照极角从小到大排序，遇到极角相同的两个点，如果这两个点的极角不比其他所有点小，则将与极点的距离大的排在前面，否则将与极点的距离小的排在前面。

对于排序完的序列，从极点出发连向第一个点，再顺次连向后面的点，最后回到极点，就得到了一个简单的多边形。

const int maxp=111;
struct Polygon{
    int n;
    Point p[maxp];
    Polygon(){n=0;}
    void add(Point q){p[n++]=q;}
    struct cmp{
        Point p;
        cmp(const Point &p0){p=p0;}
        bool operator()(const Point &aa,const Point &bb){
            Point a=aa,b=bb;
            int d=dcmp(det(a-p,b-p));
            if (d==0) return dcmp((a-p).norm()-(b-p).norm())<0;
            return d>0;
        }
    };
};

水平排序

水平排序按照下面的规则，点按照Y坐标递增，Y坐标相同时X坐标递增的顺序排序。取排序后第一个点为A，最后一个点为B，按照顺序取出向量AB右侧的点，在按照反序取出向量AB左侧的点，两个序列连接起来就是最终排序的序列。

水平排序虽然比极角排序更为复杂，但是不涉及三角函数的运算，所以精度更好。

寻找凸包

基本概念

点集Q的凸包是一个最小的凸多边形P，满足Q中的每个点或者在P的边界上，或者在P的内部。我们用CH(Q)来表示Q的凸包。

如果把点想象成木板上的钉子，那么凸包就是包围了所有钉子的拉紧了的橡皮筋。

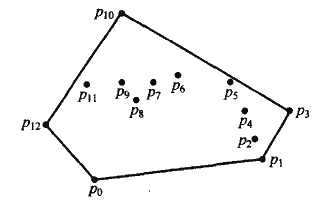
这里介绍计算凸包的两种常用算法。它们都按逆时针方向的顺序输出凸包的各个顶点。

第一种算法称为Graham扫描法，运行时间为O(nlogn)。第二种算法称为Jarvis步进法，运行时间为O(nh)，h为凸包中的顶点数。

其它可以在O(nlogn)时间内计算凸包的方法有增量方法、分治法、剪枝搜索方法。

计算一组点的凸包本身就是一个很有趣的问题，并且很多计算几何的算法都依赖凸包的计算，比如二维最远点对问题等。

Graham扫描法

Graham算法可以用来求解简单多边形的凸包。运用点的有序化过程可以将无序的点集转化为简单多边形，从而可以讲算法运用到任意点集上。

算法通过维护一个关于候选点的栈S来解决凸包问题。输入集合Q中的每个点都被压入栈一次，非CH(Q)中顶点的点最终被弹出栈。当算法终止时，栈S中仅包含CH(Q)中的顶点，其顺序为各点在边界上出现的逆时针方向排列的顺序。

算法初始时取一个肯定在凸包上的点加入栈中，可取最左下角的点，之后从初始点的下一个点开始，按照顺序将每个点加入栈顶，如果栈顶的三个顶点A、B、C不能保证凸性，即(向量BC)X(向量AB)<0时，则退栈，直到将所有顶点都处理一遍为止。

Graham算法还有一个增强版的算法Andrew。Andrew算法是基于水平序的。首先把所有点按照x从小到大排序，x相同则按照y从小到大排序。删除重复点，得到序列p1，p2...

把p1和p2放到凸包中。从p3开始，当新点在凸包前进的方向的左边时继续，否则依次删除最近加入凸包的点，直到新点在左边，最终得到了一个下凸包。

然后反过来从pn开始再做一次，求出上凸包，合并起来就是完整的凸包。

左右扫描一次的复杂度是O(n)，加上排序后的复杂度为O(nlogn)。

void Andrew(Polygon &Q,Polygon &S){
    int i;
    int n=Q.n;
    sort(Q.p,Q.p+n);
    S.n=n;
    for (i=0;i<min(n,2);i++) S.p[i]=Q.p[i];
    if (n<=2)return;
    int &top=S.n;
    top=1;
    for (i=2;i<n;i++){
        while (top&&det(S.p[top]-Q.p[i],S.p[top-1]-Q.p[i])<=0) top--;
        S.p[++top]=Q.p[i];
    }
    int temp=top;
    S.p[++top]=Q.p[n-2];
    for (i=n-3;i>=0;i--){
        while (top!=temp&&det(S.p[top]-Q.p[i],S.p[top-1]-Q.p[i])<=0) top--;
        S.p[++top]=Q.p[i];
    }
}

Jarvis步进法

Jarvis步进法运用了一种称为打包的技术来计算一个点集Q的凸包。算法的运行时间为O(nh)，其中h是CH(Q)的顶点数。当h为o(logn)时，Jarvis步进法在渐进意义上比Graham扫描法的速度更快。

可以把Jarvis步进法想象成在集合Q的外面紧紧的包了一层纸。开始时，把纸的末端粘在集合中最低的点上，即粘在与Graham扫描法开始时相同的点p0上。该点为凸包的一个顶点。把纸拉向右边使其绷紧，然后再把纸拉高一些，直到碰到一个点。该点也必定是凸包的一个顶点，这个过程可以在以p0为原点的极角坐标系中比较其他的点，用O(n)复杂度解决。使纸保持绷紧状态，用这种方法继续围绕顶点集合，直至回到原始点p0。这样一共h步，得到了h个点，h为凸包上的点数，所以总的复杂度就是O(nh)。

寻找最近点对

基本概念

考虑在n>=2个点的集合Q中寻找最近点对的问题。最近是指欧几里得距离：即，点p1=(x1,y1)和p2=(x2,y2)之间的距离为sqrt((x1-x2)²+(y1-y2)²)。集合Q中两个点可能重合，在这种情况下，它们之间的距离为0。在暴力枚举最近点对的算法中，要查找O(n²)个点对。它还有一个用分治的复杂度O(nlogn)的经典解法。

分治算法

算法的每一次递归调用的输入为子集P和数组X和Y，每个数组均包含输入子集P的所有点。对数组X中的点，按其x坐标单调递增的排序，对数组Y中的点按其y坐标单调递增的顺序进行排序。不能在每次递归调用中进行排序，我们用预排序保持这种排序性质。

输入为P、X和Y的递归调用首先检查是否|P|<=3。如果是，则直接对所有的点进行检查，并返回最近点对。如果|P|>3，则递归调用执行如下分治法：

分解：找出一条垂直线L，它把点集P划分为满足下列条件的两个集合P_L和P_R：两个子集中的元素是P的一半，P_L中所有点都在线L上或左侧，P_R中的所有点都在线L上或右侧。数组X被划分为两个数组X_L和X_R，分别包含P_L和P_R中的点，并按x坐标单调递增的顺序进行排序。

解决：把P划分为P_L和P_R后，再进行两次递归调用，一次找出P_L中最近点对，一次找出P_R中的最近点对。第一次调用的输入为子集P_L，数组X_L和Y_L；第二次为P_R，X_R，Y_R。设对P_L和P_R，返回的最近点对的距离分别为δ_L和δ_R，则置δ=min(δ_L，δ_R)。

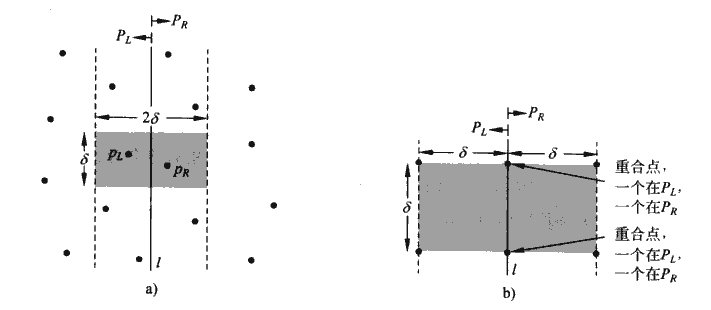
合并：最近点对要么是某次递归调用找出的距离为δ的点对，要么是P_L中的一个点与P_R中的一个点组成的点对，算法确定是否存在其距离小于δ的一个点对。如果存在这样的一个点对，则点对中的两个点必定都在直线L的δ单位之内。因此，它们必定都处于以直线L为重心、宽度为2δ的垂直带形的区域内。为了找出这样的点对，要做如下工作：

1. 建立一个数组Y'，它是把数组Y中所有不在宽度为2δ的垂直带性区域内的点去掉后所得的数组。数组Y'与Y一样，是按y坐标顺序排序的。
2. 对数组Y'中的每个点p，算法试图找出Y'中距离p在δ单位以内的点。下面将会看到，在Y'中仅需考虑紧随p后的7个点。算法计算出从p到这7个点的距离，并记录下Y'的所有点对中，最近点对的距离δ'。
3. 如果δ'<δ，则垂直带形区域内，包含比递归调用找到的最近距离更近的点对，于是返回该点对以及其距离δ'。否则，就返回递归调用过程中发现的最近点对距离δ。

上述描述中，省略了一些重要的实现细节。

为了能快速的生成按y坐标排序的数组Y_L和Y_R，我们线性的扫描数组Y中的点，如果一个点在P_L中，则把它添加到数组Y_L的末端，否则添加到数组Y_R的末端。

如何对点进行预排序，在第一次递归调用前，对所有的点进行排序。这些排序数组被传递到第一次递归调用中，根据需要在递归调用时用线性扫描对其进行分割。