无穷级数就像高中的数列一样,但是却要我们钻研的方向不同,高中叫我们求收敛于什么,大学里让我们研究收敛性。

假设Sn的趋于无穷的极限存在则称Sn收敛,不存在则叫做发散,收敛时Sn+1-Sn 叫做余和,余和为0。
这里举出一些常用的级数收敛条件:
等比级数: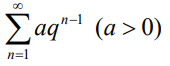 {当q>=1时级数发散,当0<q<1时级数收敛}
{当q>=1时级数发散,当0<q<1时级数收敛}
p级数: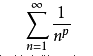 和等比级数恰恰【相反】{当p>1时级数收敛,p<1时级数发散}
和等比级数恰恰【相反】{当p>1时级数收敛,p<1时级数发散}
调和级数: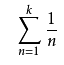 从形式上就可以看出这是p级数的特殊形式,那么理所当然这里就是发散的
从形式上就可以看出这是p级数的特殊形式,那么理所当然这里就是发散的
这三个级数是比较基本的级数,在判断一些复杂级数的敛散性时要借助这三个级数来辅助判断



接下来说一些级数的基本性质:
- 线性:

- (个人称之为稳定性~~~)

- (个人称之为可拆性~~~)

这虽然时基本性质,但再特殊的性质也是从基础出发的,所以要记牢这三个性质!!!
接下来谈谈级数收敛的必要条件(终于讲怎么证明了~,注意这里是必要不是充要!!)

这里的关系可以这么理解,级数的和要是收敛的话,假设就等于一个固定有限的值,这个值要给无穷多的数分,就像让全世界饥渴的跳蚤去吸食一只干瘦的牛犊一样,每只跳蚤吸到的血几乎为0;
现在换个角度看,就是从跳蚤的角度看,每只跳蚤单独吸到的血都趋于0,但是这些跳蚤在一起吸食时(一起合作)在吸食到一定程度时中变异了,仿佛有了替身能力一般,跳蚤们可以将牛血反复复制,从而造出无穷无尽的牛血。这便是即使
每一项的极限为0,但是一起行动时引起了质变,导致了无穷级数的和的发散;
那么假如是蚂蝗而且吸得是医院的血库,那蚂蝗一边在吸,医院一边又在供给,就像服务员给乘客递上葡萄酒和鱼子酱那样的给蚂蝗供血,可想而知蚂蝗吸得血将会是无穷大!!!!
正项级数,也是研究的比较多的级数,我直接放定义先了

这个很明显就是缩小了讨论范围了,现在只讨论正数了,但是这就像是和蝉一起埋在地底的树根一样,越分支越多,接下来要学的只会更多。
下面开始研究正项级数敛散性的判别法
第一种是比较判别法:

这种判别法显而易见,就是上面那个跳蚤和蚂蝗的例子vn就是蚂蝗,un则是跳蚤,要是连蚂蝗vn不能像夸父喝干黄河水一样得喝干牛犊的血的话,因为跳蚤 比蚂蝗小![]() ,那么跳蚤un也不能喝完牛犊身上的血
,那么跳蚤un也不能喝完牛犊身上的血![]() ;相反要是连跳蚤都可以喝完的话,那么蚂蝗也一定可以喝完牛犊的血
;相反要是连跳蚤都可以喝完的话,那么蚂蝗也一定可以喝完牛犊的血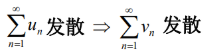
换一种极限的形式来看:

第二种判别法是比值判别法:

P.S. 这里要注意公式里的内容,比较判别法里面的极限形式和这个很像,但是比值判别法是前一项和后一项的对比,换句话说,正项级数要是项递减的话就是收敛的,递增的话就是发散的。好比《JOJO石之海》里的绿色婴儿,你在靠近绿色婴儿的过程中自己一直在减小一半,这样的话你永远也达不到绿色婴儿,只能无限接近。


第三种判别法是根值判别法:

这和比值判别法更进一步,从比较判别法到根值判别法,参与比价的项越来越小,比较判别法需要自己和别人比,比值判别法需要自己和自己兄弟比,而根值则像一个成天看初音未来的宅男一样窝在家里有一套自己的标准,自己给自己做决定。
例题:![]()

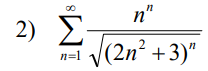
![]()
接下来说的是积分判别法,用的貌似不多,多学一种总是好的嘛: 
例题:
![]()
![]()
终于来到任意项了,这里又要多讨论一种级数了
交错级数:

这里用到了新的判别法:莱布尼兹判别法

简单来说就是把所有项都取绝对值后,要是呈现出递减趋势的话,那么交错级数就是收敛的(当然不能忘了通项趋于0这个必要条件)
例题:

第二个知识点是绝对收敛和条件收敛

![]()
绝对收敛就像是掉进粪池的钻石一样,绝对值就是粪池,级数本身是钻石,钻石掉进粪池(加上绝对值)依然具有价值(级数依然收敛);
条件收敛却像空姐小推车里的新鲜鱼子酱一样,本身具有价值(收敛),但是掉进粪池(加上绝对值),就失去了价值(级数发散)。
例题:

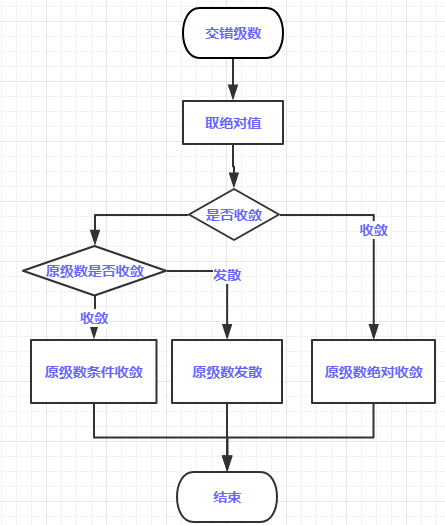
函数项级数是接下来幂级数的基本概念,所以对函数项级数要有正确的认识



这是无穷级数里很重要的内容
首先是个很重要的定理:abel定理

这个x0感觉就像是替身的射程距离,在这个距离内我绝对能够欧拉你,超出这个距离,我就欧拉不到你了。
推论:

接下来理所当然要学的是收敛半径的求法

对于这个形式的级数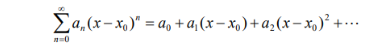
可以用y0=x-x0代替,转化成abel定理的形式
例题:
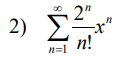
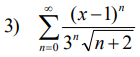
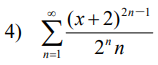
提示:一些题目像第四题可以直接用比值判别法得到ρ,然后用ρ和1比大小求出x的取值范围,再在端点处特殊处理
这是另外一方法,择优做题

接下来讲一些幂级数的分析性质:




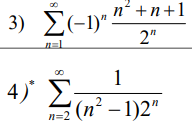
泰勒级数:

函数要等于它的泰勒级数的充分必要条件是余项等于0


常用的泰勒级数要记牢,做题会经常用到

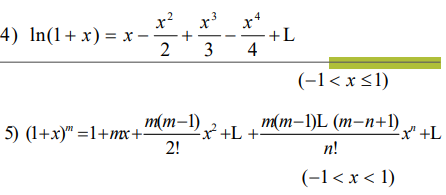

由于幂级数收敛于一个值速度太慢,在工程上人们常用傅里叶级数来进行近似,它收敛的速度很快
三角级数:三角函数任意两个具有正交性

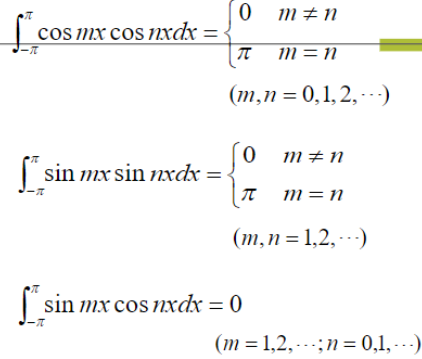






![]()



