17.10.01

• 上午
  • 模拟考试
    • Prob 1（AC）.水水最短路，用优先队列优化SPFA
    • Prob 2（崩溃一半）.一个区间dp，我用的记忆化搜索，结果数据范围看错，数组开小了……

      但题还不错，蓝书原题吧：

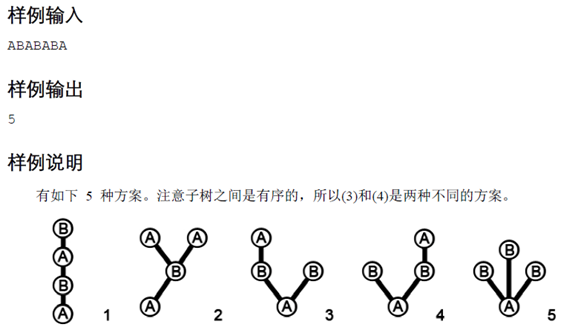
      给出一颗树的遍历序列，只要遇到一个节点，无论之前是否遇到过，都加入序列，求有多少种不同的树可以生成该序列(答案对1e9取模)。

      

      字符串的长度不超过300（考试看成200了，555）

      考虑一个序列区间，若左端点L的值等于右端点R的值，则该值为该区间的根的值。

      显然这个根可以有多个儿子，但由于序列的特殊性，每次遍历完一个儿子，都会回到根，即对于该序列区间中间的某个i位置的值若等于根的值，则表明L+1~i-1可以是根的第一个儿子的遍历序列，对于这个小区间，可以递归做相同的操作。至于剩下的i~R表示对根的剩下的儿子的遍历，也做相同的递归操作即可，然后用乘法原理把两端的方法数相乘，累加进该区间的答案。

      转移式：（dp[l][r]表示l~r区间的方法数）

      代码：

      #include<cstdio>
      #include<cstring>
      #include<iostream>
      using namespace std;
      const int mod=1000000000;
      char s[305];
      int dp[305][305],ls;
      int search(int l,int r){
      	int &now=dp[l][r];
      	if(now!=-1) return now;
      	if(s[l]!=s[r]||l+1==r||l>r) return now=0;
      	if(l==r) return now=1;
      	now=0;
      	for(int i=l+1;i<=r-1;i++)
      		if(s[i]==s[l]) now=(1ll*now+1ll*search(l+1,i-1)*search(i,r))%mod;
      	now=(1ll*now+1ll*search(l+1,r-1))%mod;
      	return now;
      }
      int main(){
      	freopen("probe.in","r",stdin);
      	freopen("probe.out","w",stdout);
      	memset(dp,-1,sizeof(dp));
      	scanf("%s",s+1); ls=strlen(s+1);
      	printf("%d",search(1,ls));
      	return 0;
      }

    • Prob 3（TLE）.一个状压DP，但在取答案时思路卡住了，只过了50%的数据，但大佬们曰了一下后，我发现实际上只改一点点就可以过了，诶。
  • 又趁着考试没结束打了一个水水题
    • 入门OJ 2039: [Noip模拟题]抽奖

      递推，令dp[i][j]表示买了i次票，共买到j张不同的票
      然后就很好转移了，
      当dp[*][n-1]转移dp[*][n]时，把dp[*][n]累加进答案

      代码：

      #include<cstdio>
      #include<cstring>
      #include<iostream>
      using namespace std;
      double dp[1005][1005],ans;
      int n,m;
      int main(){
      	scanf("%d%d",&n,&m);
      	dp[1][1]=1;
      	for(int i=2;i<=m;i++)
      		for(int j=1;j<=min(i,n);j++){
      			if(j!=n) dp[i][j]+=dp[i-1][j]*(1.0*j/n);
      			dp[i][j]+=dp[i-1][j-1]*(1.0*(n-(j-1))/n);
      			if(j==n) ans+=dp[i][j];
      		}
      	if(n==1) printf("1.0000");
      	else printf("%.4lf",ans);
      	return 0;
      }
      

• 下午
  • 入门OJ 2 道
    • 入门OJ 2040: [Noip模拟题]最短路径建图。
    由于相邻层次间的点点可以相互通达。
    n*n的代价对相邻层次的点暴力建边？tan90°
    在对层次新添加两个点：
    一个"带领"该层次的点走出去;
    一个"接受"外来的点；
    然后直接对相邻层次的新添加的点连边即可。注意：每个层次一定要新添加两个点，只添加一个的话会有错的。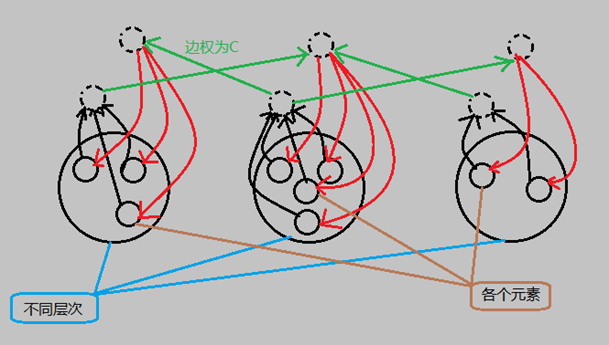
    跑个最短路就出来了。

    #include<queue>
    #include<cstdio>
    #include<cstring>
    #include<iostream>
    #define INF 0x3f3f3f3f
    #define MAXN 100005
    #define node(a,b) (node){a,b}
    using namespace std;
    struct node{
    	int id,d;
    	bool operator <(const node &rtm) const{
    		return d>rtm.d;
    	}
    };
    struct edge{
    	int to,next,val;
    }e[MAXN*8];
    int dis[3*MAXN];
    int head[3*MAXN];
    bool inq[3*MAXN];
    int n,m,ent,c;
    void add(int u,int v,int w){
    	e[ent]=(edge){v,head[u],w};
    	head[u]=ent++;
    }
    void spfa(){
    	memset(dis,0x3f,sizeof(dis));
    	priority_queue<node>q; node u; int v;
    	q.push(node(1,0)); dis[1]=0; inq[1]=1;
    	while(!q.empty()){
    		u=q.top(); q.pop(); inq[u.id]=0;
    		for(int i=head[u.id];i;i=e[i].next){
    			v=e[i].to;
    			if(dis[v]<=dis[u.id]+e[i].val) continue;
    			dis[v]=dis[u.id]+e[i].val;
    			if(inq[v]) continue;
    			q.push(node(v,dis[v]));
    			inq[v]=1;
    		}
    	}
    }
    int main(){
    	int T,cas=0; scanf("%d",&T);
    	while(T--){
    		ent=1; cas++;
    		memset(head,0,sizeof(head));
    		scanf("%d%d%d",&n,&m,&c);
    		for(int i=1,a;i<=n;i++){
    			scanf("%d",&a);
    			add(i,a+n,0);add(2*n+a,i,0);
    		}
    		for(int i=1;i<n;i++) 
    			add(n+i,2*n+i+1,c),add(n+i+1,2*n+i,c);
    		for(int i=1,a,b,d;i<=m;i++){
    			scanf("%d%d%d",&a,&b,&d);
    			add(a,b,d); add(b,a,d);
    		}
    		spfa();
    		int ans=dis[n]!=INF?dis[n]:-1;
    		printf("Case #%d: %d
    ",cas,ans);
    	}
    	return 0;
    }
    

  • 入门OJ 2041 [Noip模拟题]序列若 i~j区间 是满足条件的，
    那么 j+1要满足什么条件才合法呢，即i~j+1满足条件？
    显然第j+1个元素需要满足 r[j+1]>=max(l[k]|i<=k<=j)
       
    用单调队列维护当前区间的l的最大值，
    进行区间头部的移动直到当前元素满足条件。
  代码：

  #include<cstdio>
  #include<cstring>
  #include<iostream>
  using namespace std;
  int l[1000005],r[1000005],q[1000005]; 
  int head=1,tail=0,ans,n,be;
  int main(){
  	scanf("%d",&n);
  	for(int i=1;i<=n;i++){
  		scanf("%d%d",&l[i],&r[i]);
  		while(head<=tail&&l[q[head]]>r[i]) be=q[head],head++;
  		while(head<=tail&&l[q[tail]]<l[i]) tail--;
  		ans=max(ans,i-be);
  		q[++tail]=i;
  	}
  	printf("%d",ans);
  	return 0;
  }

• 晚上
• 感受绝望……
• 入门OJ 2043: [Noip模拟题]小Y的炮

• 想了一个比较暴力的贪心，但觉得会TLE

  看题解，然后看不懂……

  半个小时后，经过大佬提点，终于懂了:

  去掉冗余大炮后，则剩下的大炮随着a值的上升，b值在下降

  因为大炮不超过500个，大炮的射击距离不超过500，所以我么可以预处理出某些高度用贪心的方法轰平需要几次。

  那么需要处理哪些呢？

  

  然后就没了……

  写了一个离散化版的，无限WA，而且又对拍不出错误，绝望……

• End：
• 考试还是不细心啊， 看错数据范围白白丢掉50分！！！
• 代码能力不够呢，看看绝望的晚上，知道了方法却AC不了，心痛。