Ural1057

题目大意

求给定区间[X,Y]中满足下列条件的整数个数：这个数恰好等于K个互不相等的B的整
数次幂之和。例如，设X=15，Y=20，K=2，B=2，则有且仅有下列三个数满足题意：
                          

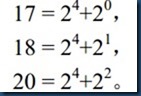
输入：第一行包含两个整数X和Y。接下来两行包含整数K和B。
输出：只包含一个整数，表示满足条件的数的个数。
数据规模：1 ≤ X ≤ Y ≤ 2^31
−1，1 ≤ K ≤ 20，  2 ≤ B ≤ 10。

题解

《浅谈数位类统计问题》的论问题~~~~~人生第一道数位DP，哈哈~~~O(∩_∩)O~~代码纯属抄袭~~~~

代码：

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <string>
using namespace std;
#define MAXN 35
int f[MAXN][MAXN];
void init()
{
    f[0][0]=1;
    for(int i=1;i<32;i++)
    {
        f[i][0]=f[i-1][0];
        for(int j=1;j<=i;j++)
            f[i][j]=f[i-1][j]+f[i-1][j-1];
    }
}
int change(int x,int b)
{
    int p[MAXN];
    int ans=0;
    while(x)
    {
        p[ans++]=x%b;
        x/=b;
    }
    reverse(p,p+ans);
    for(int i=0;i<ans;i++)
        if(p[i]>1)
        {
            for(int j=i;j<ans;j++)
                p[j]=1;
            break;
        }
        for(int i=0;i<ans;i++)
            x=x|(p[ans-i-1]<<i);
        return x;
}
int cal(int x,int k)
{
    int tot=0,ans=0;
    for(int i=31;i>0;i--)
    {
        if(x&(1<<i))
        {
            tot++;
            if(tot>k) break;
            x=x^(1<<i);
        }
        if((1<<(i-1))<=x)
            ans+=f[i-1][k-tot];
    }
    if(tot+x==k) ans++;
    return ans;
}
int main()
{
    init();
    int x,y,k,b;
    while(cin>>x>>y>>k>>b)
    {
        int X=change(x,b);
        int Y=change(y,b);
        cout<<cal(Y,k)-cal(X-1,k)<<endl;
    }
    return 0;
}