EM
1. 基本问题
EM算法是解决带有隐变量模型的方法,基本的模型假设为
由于引入了隐变量
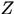
,使得我们无法通过对
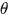
求偏导得到最优解。
2. 推导
根据jesen不等式,对于凹函数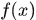 ,有
,有
其中,
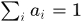
,当且仅当
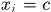
时,“=”成立。而
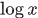
是凹函数,因此
且
时,等号成立,取得最紧的下界。
也即
因此,当取得最紧的下界时,任何使得下界提升的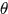 都能使
都能使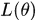 提升
提升
3. 算法流程
输入:观测变量数据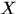 ,隐变量数据
,隐变量数据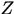 ,联合分布
,联合分布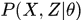 ,条件分布
,条件分布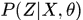
输出:模型参数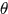
(1)选择参数的初值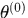
(2)E step: 计算在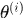 下最紧的下界
下最紧的下界
(3)M step: