牛客练习赛28 E迎风舞 （三分查找）

链接：https://www.nowcoder.com/acm/contest/200/E
来源：牛客网

时间限制：C/C++ 1秒，其他语言2秒
空间限制：C/C++ 262144K，其他语言524288K
Special Judge, 64bit IO Format: %lld

题目描述

女装会成瘾

由于某人的精心设计，小可爱掉入了女装的天坑无法自拔。

于是……她开始疯狂的成批的买女装。

而Kirito_Rivaille为了戒掉他的女装病，准备实施家暴——把小可爱的女装从窗户扔下去

他们家距离地面的高度为H，也就是说，女装都是从这了被抛出去的。

而由于Kirito_Rivaille体力有限，(女装也很沉)，所以她抛出去的速度最大是v(最小是0);

之后呢，Kirito_Rivaille为了不让小可爱在下去捡到，于是想尽可能的抛的远一点。

所以现在他想找个合适的角度抛出。

作为Kirito_Rivaille身边的活宝，你的任务是帮助Kirito_Rivaille。

给出他们俩住的屋子的高度H和抛出速度v，请你找到一个合适的角度θ使得落地时距他们脚下的地面(H=0的位置)的直线距离最远。

然而小可爱并不关心这个角度是多少，只关心距离他们的直线距离是多少。

输出四舍五入保留五位小数，当你的答案与std的相对误差不超过0.00001时就算正确了。

说明：不考虑空气阻力，g取9.80665。

提示公式：

    x=vtcosθ,

    y=H+vtsinθ-0.5*gt²

其中t为飞行时间。

输入描述:

第一行一个正整数T

接下来T行每行两个实数H,v

输出描述:

T行每行一个数，保留五位小数。

解题思路：题目给出了我们要推的式子

　　x=vtcosθ,

       y=H+vtsinθ-0.5*gt²

将y=0带入第2个式子得出时间t

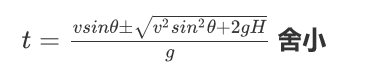
将t再带入第1个式子，得出水平距离x随时间t变化的函数

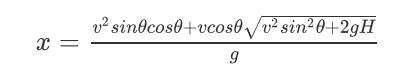
然后，会求导的求导，不会的根据窝们的常识，扔东西的时候，随着我们的角度增加，距离式先变大在变小的。
一个单峰函数求最值的问题，三分的模板：https://blog.csdn.net/littlewhite520/article/details/70144763

附上代码：

#include<bits/stdc++.h>
using namespace std;
const double eps=1e-6;
const double g=9.80665;
const double pi2=1.570796327;
double H,v;
double f(double th)
{
    return (v*sin(th)+sqrt(v*v*sin(th)*sin(th)+2*g*H))*v*cos(th)/g;
}
void three_divide()
{
    double l=0,r=pi2;
    while(r-l>=eps)
    {
        double mid1=l+(r-l)/3.0;
        double mid2=r-(r-l)/3.0;
        if(f(mid1)<=f(mid2))
            l=mid1;
        else
            r=mid2;
    }
    printf("%.5lf
",f(l));
}

int main()
{
    int T;
    scanf("%d",&T);
    while(T--)
    {
        scanf("%lf%lf",&H,&v);
        three_divide();
    }
    return 0;
}