题意
在一个网格上,你要从((0,0))走到((n,n)),每一步只能向上或向右,且不能越过对角线,也不能经过网格上的(c)个给定的点,求方案数( mod (10^9+7))
(nleq 100000,cleq 1000)
Solution
这个题比赛时没认真想,就写了(O(n^2))的暴力,但是这部分分和正解毫无联系,想要推出正解还是要从(c=0)的部分分入手。
- (c=0),打个表就能发现答案是(C_{2n}^{n}-C_{2n}^{n-1})。
(C_{2n}^{n})好解释,就是((0,0))走到((n,n))一共走了(n)步其中选(n)步横着走的方案数。
(C_{2n}^{n-1})是个什么鬼?我借题解一幅图讲讲:
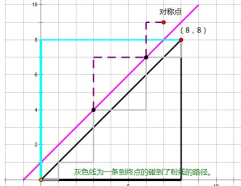
也就是说((0,0))走到((n,n))的每一条不合法路径,都可以一一对应到((0,0))走到((n-1,n+1))的一条路径,而((0,0))走到((n-1,n+1))是只有(n-1)步能横着走的,所以对应路径条数就是(C_{2n}^{n-1})。
然后答案就是(C_{2n}^{n}-C_{2n}^{n-1})。
正解是这样的:
将((n,n))也当做关键点,把所有关键点按照(x)从小到大排序,如果(x)相同则按(y)从小到大排序。
设(f_i)表示从((0,0))走到第(i)个关键点,但不经过在(i)左下方其他的关键点的方案数,(g(x_1,y_1,x_2,y_2))表示((x_1,y_1))走到((x_2,y_2))的所有不越过对角线的路径数。
转移:
(f_i=g(0,0,x_i,y_i)-sum_{j=1}^{i-1}[x_jleq x_i and y_jleq y_i]f_j*g(x_j,y_j,x_i,y_i))
怎么理解这个转移呢,首先(g(0,0,x_i,y_i))是总的方案数,然后我们枚举(i)左下角的点,这个点不论怎么走到(i),这样的路径都是不合法的,要在答案里减掉。
这么算为什么不重不漏呢?
不重复是显然的。
不漏可以这样想,对于每一条((0,0))到(i)不合法的路径,都会经过(i)左下角区域里的某个关键点,设遇到的第一个关键点是(j),由于我们保证了(f_j)是不经过在(j)左下方其他的关键点的方案数。所以,枚举所有在(i)左下方的(j)作为不合法路径上的第一个点,就能算出所有不合法路径方案数,也就推出了合法路径方案数。
那么(g)的求法?
同样考虑用总方案减去不合法方案。
如果(x_2<x_1)或者(y_2<y_1),显然(g(x_1,y_1,x_2,y_2)=0)。
否则,记(x=x_2-x_1),(y=y_2-y_1),则(g(x_1,y_1,x_2,y_2)=C_{x+y}^{x}-g(x_1,y_1,y_2-1,x_2+1))
(C_{x+y}^{x})是总共的方案。
我们可以依照(c=0)的做法,发现((x_1,y_1))到((x_2,y_2))的每一条跨越对角线的路径,都一一对应着((x_1,y_1))到((y_2-1,x_2+1))的一条路径。
((y_2-1,x_2+1))其实是((x_2,y_2))关于直线(y=x+1)的对称点,因此就能把不合法路径一一对应。
这样就解释了(g)的求法。
线性预处理逆元,就能(O(1))求组合数,总复杂度(O(c^2))
Code
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long ll;
const int N = 200007, M = 1007;
const ll P = 1e9 + 7;
int n, c;
ll inv[N], fac[N], f[M];
struct point { int x, y; } p[M];
int cmp(point a, point b) { return a.x == b.x ? a.y < b.y : a.x < b.x; }
ll C(int n, int m) { return 1ll * fac[n] * inv[m] % P * inv[n - m] % P; }
ll getway(int x1, int y1, int x2, int y2)
{
if (x2 < x1 || y2 < y1) return 0;
int x = x2 - x1, y = y2 - y1;
return C(x + y, x);
}
ll way(int x1, int y1, int x2, int y2)
{
int x = y2 - 1, y = x2 + 1;
return (getway(x1, y1, x2, y2) - getway(x1, y1, x, y) + P) % P;
}
void init()
{
scanf("%d%d", &n, &c);
fac[0] = 1; for (int i = 1; i <= 2 * n; i++) fac[i] = fac[i - 1] * i % P;
inv[1] = 1; for (int i = 2; i <= 2 * n; i++) inv[i] = (P - P / i) * 1ll * inv[P % i] % P;
inv[0] = 1; for (int i = 1; i <= 2 * n; i++) inv[i] = inv[i] * inv[i - 1] % P;
for (int i = 1; i <= c; i++) scanf("%d%d", &p[i].x, &p[i].y);
p[++c] = (point){n, n};
sort(p + 1, p + c + 1, cmp);
}
void solve()
{
for (int i = 1, sum; i <= c; i++)
{
f[i] = way(0, 0, p[i].x, p[i].y), sum = 0;
for (int j = 1; j <= i - 1; j++) if (p[j].x <= p[i].x && p[j].y <= p[i].y) sum = (sum + 1ll * f[j] * way(p[j].x, p[j].y, p[i].x, p[i].y) % P) % P;
f[i] = (f[i] - sum + P) % P;
}
printf("%lld
", f[c]);
}
int main()
{
init();
solve();
return 0;
}