20172325《Java程序设计》第一周学习总结

20172325《Java程序设计》第一周学习总结

教材学习内容总结

第一章

1.1软件质量

• 软件工程是一门关于高质量软件开发的技术和理论的学科。
• 高质量软件的特征
  

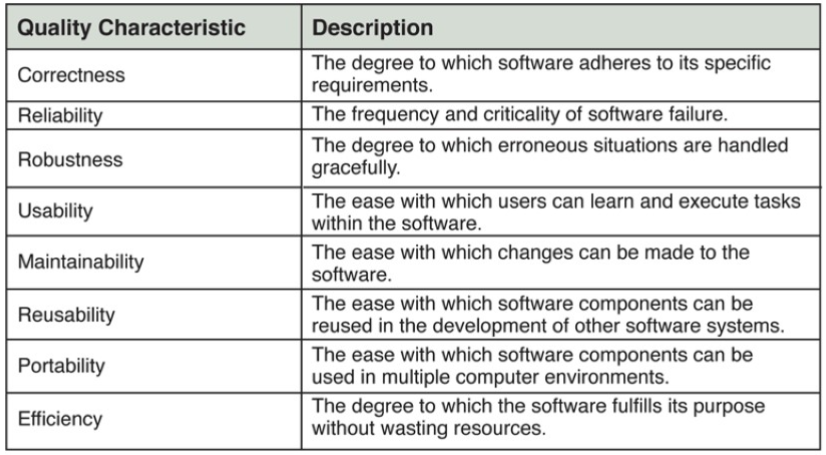
1.2 数据结构

• 软件开发的目的是构建软件，而不仅仅是编写代码。
• 栈可用于颠倒数据集的顺序；队列可以保持其数据的顺序

第二章

2.1 算法效率分析
为完成某一特定任务所使用的算法的效率，是决定一个程序运行速度的主要因素
2.2 增大函数与大O记法

• 增长函数表示了该算法的时间复杂度或空间复杂度

• 我们主要讨论算法的渐进复杂度，渐进复杂度称为算法的阶次（忽略该算法的增长函数中的常量和其他次要项，只保留主项而得出的）
  

• 算法的阶次为增长函数提供了一个上界

• 所有具有相同阶次的算法，从运行效率的角度来说都认为是等价的

2.3 增长函数的比较

• 寻求一个更高效的算法是一种比使用更快处理器的更好解决方法
• 增长函数的比较
  
  

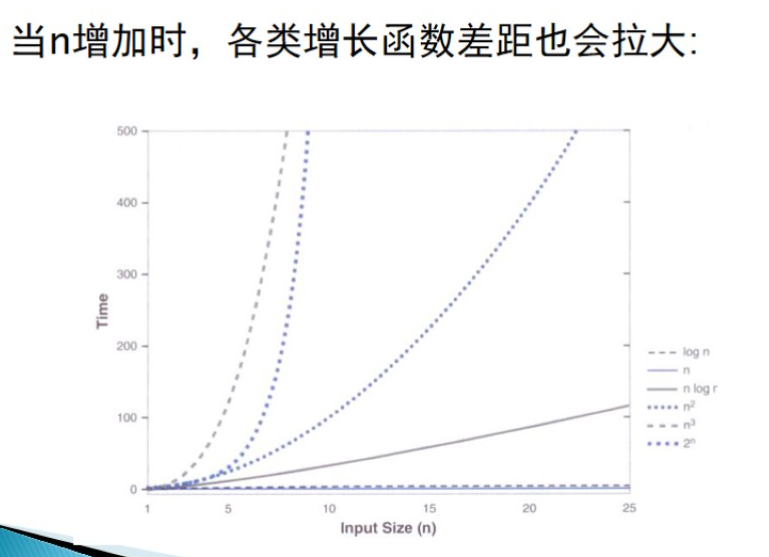
2.4 时间复杂度分析

• 循环的时间复杂度等于循环体的复杂度乘以该循环运行的次数；
• 分析嵌套循环的复杂度时，必须将内层循环和外层循环都考虑进来。

教材学习中的问题和解决过程

暂无

课本习题解答

• EX2.1 下列增长函数的阶次是多少？

  • a.10n^2+100n+1000
  • 解：O(n^2)
  • b.10n^3-7
  • 解：O(n^3)
  • c.2ⁿ⁺¹⁰⁰ⁿ3
  • 解：O(2^n)
  • d.n^2 ·log2(n)
  • 解：O(n^2 ·log2(n))

• EX2.4 请确定下面代码段的增长函数和阶次：

for(int count = 0 ; count < n ; count++)
    for(int count2 = 0 ; count2 < n ; count2 = count2 + 2)
    {
        System.out.println(count,count2);
    }
}

- 解：嵌套循环，内层循环的循环次数是n/2，外层循环的循环次数是n，所以增长函数为：F(n)=(n^2)/2，阶次为O(n^2)。

• EX 2.5：请确定下面代码段的增长函数和阶次:

for(int count = 0 ; count < n ; count++)
    for(int count2 = 1 ; count2 < n ; count2 = count2 * 2)
    {
        System.out.println(count,count2);
    }
}

- 解：嵌套循环，内层循环的循环次数是logn，外层循环的循环次数是n，所以增长函数为：F(n)=nlog2(n)，阶次为O(n·log2(n))。

代码托管

本周无代码

结对及互评

• 本周结对学习情况
  • 20172306
  • 结对学习内容
    • 一起学习了第一、二章的内容；
    • 针对上课时老师所讲内容进行了讨论；

其他（感悟、思考等，可选）

新学期开始，希望能够弥补上学期没有学到位的知识，同时与老师和结对伙伴一起顺利完成新一个学期的学习内容。

学习进度条

	代码行数（新增/累积）	博客量（新增/累积）	学习时间（新增/累积）
目标	5000行	30篇	400小时
第一周	0/0	1/1	8/8

参考资料

• Java程序设计教程

• 《Java软件结构与数据结构(第4版)》