题目
题目描述
司令部的将军们打算在N*M的网格地图上部署他们的炮兵部队。一个N*M的地图由N行M列组成,地图的每一格可能是山地(用“H” 表示),也可能是平原(用“P”表示),如下图。在每一格平原地形上最多可以布置一支炮兵部队(山地上不能够部署炮兵部队);一支炮兵部队在地图上的攻击范围如图中黑色区域所示:
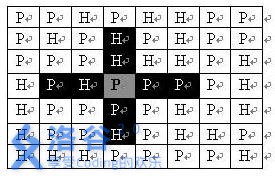
如果在地图中的灰色所标识的平原上部署一支炮兵部队,则图中的黑色的网格表示它能够攻击到的区域:沿横向左右各两格,沿纵向上下各两格。图上其它白色网格均攻击不到。从图上可见炮兵的攻击范围不受地形的影响。 现在,将军们规划如何部署炮兵部队,在防止误伤的前提下(保证任何两支炮兵部队之间不能互相攻击,即任何一支炮兵部队都不在其他支炮兵部队的攻击范围内),在整个地图区域内最多能够摆放多少我军的炮兵部队。
输入输出格式
输入格式:
第一行包含两个由空格分割开的正整数,分别表示N和M;
接下来的N行,每一行含有连续的M个字符(‘P’或者‘H’),中间没有空格。按顺序表示地图中每一行的数据。N≤100;M≤10。
输出格式:
仅一行,包含一个整数K,表示最多能摆放的炮兵部队的数量。
输入输出样例
分析
- 首先,显然状压DP
- 这里需要用一个数组记录下满足的数
- 减少循环
- 然后注意一点位运算多加括号
- 设f[i][j][k]为当前第i行,的集合是j,第i-1行集合是k
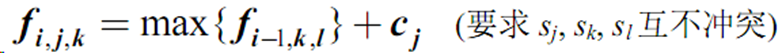
代码
#include<iostream> #define N 100000000 using namespace std; int f[100001],sta[100001]; int ff[105][1500][1500]; int sum[1500]; int b[1500]; int find(int x) { int ans=0; while (x) { ans++; x-=x&(-x); } return ans; } int main () { int m,n,xx; cin>>m>>n; char x; for (int i=1;i<=m;i++) for (int j=0;j<n;j++) { cin>>x; if (x=='P') xx=1; else xx=0; f[i]=(f[i]<<1)+xx; } int maxn=(1<<n)-1; int cnt=0; for (int i=0;i<=maxn;i++) { if (((i&(i<<1))==0)&&((i&(i>>1))==0)&&((i&(i<<2))==0)&&((i&(i>>2))==0)) b[++cnt]=i; } for (int i=0;i<=maxn;i++) sum[i]=find(i); for (int i=1;i<=n;i++) for (int j=1;j<=cnt;j++) ff[i][b[j]][0]=sum[b[j]]; for (int i=2;i<=m;i++) for (int j=1;j<=cnt;j++) if ((b[j]&f[i])==b[j]) for (int k=1;k<=cnt;k++) if ((b[k]&f[i-1])==b[k]) for (int l=1;l<=cnt;l++) if ((b[l]&f[i-2])==b[l]) { if ((b[j]&b[k])||(b[j]&b[l])||(b[k]&b[l])) continue; else ff[i][j][k]=max(ff[i-1][k][l]+sum[j],ff[i][j][k]); } int ans=0; for (int i=0;i<=maxn;i++) for (int j=0;j<=maxn;j++) ans=max(ff[n][i][j],ans); cout<<ans; }