统一下二叉树的代码格式,递归和非递归都统一格式,方便记忆管理。
三种递归格式:
前序遍历:
void PreOrder(TreeNode* root, vector<int>&path)
{
if (root)
{
path.emplace_back(root->val);
PreOrder(root->left, path);
PreOrder(root->right, path);
}
}
中序遍历:
void InOrder(TreeNode* root, vector<int>& path)
{
if (root)
{
InOrder(root->left, path);
path.emplace_back(root->val);
InOrder(root->right, path);
}
}
后序遍历:
void PostOrder(TreeNode* root, vector<int>& path)
{
if (root)
{
PostOrder(root->left, path);
PostOrder(root->right, path);
path.emplace_back(root->val);
}
}
三种递归遍历不用多解释。
三种非递归格式:
前序遍历:
void PreOrderCycle(TreeNode* root, vector<int>& path)
{
stack<pair<TreeNode*, bool>> s;
s.emplace(make_pair(root, false));
bool visited;
while (!s.empty())
{
root = s.top().first;
visited = s.top().second;
s.pop();
if (root == NULL)
continue;
if (visited)
path.emplace_back(root->val);
else
{
s.emplace(make_pair(root->right, false));
s.emplace(make_pair(root->left, false));
s.emplace(make_pair(root, true));
}
}
}
中序遍历:
void InOrderCycle(TreeNode* root, vector<int>& path)
{
stack<pair<TreeNode*, bool>> s;
s.emplace(make_pair(root, false));
bool visited;
while (!s.empty())
{
root = s.top().first;
visited = s.top().second;
s.pop();
if (root == NULL)
continue;
if (visited)
path.emplace_back(root->val);
else
{
s.emplace(make_pair(root->right, false));
s.emplace(make_pair(root, true));
s.emplace(make_pair(root->left, false));
}
}
}
后序遍历:
void PostOrderCycle(TreeNode* root, vector<int>& path)
{
stack<pair<TreeNode*, bool>> s;
s.emplace(make_pair(root, false));
bool visited;
while (!s.empty())
{
root = s.top().first;
visited = s.top().second;
s.pop();
if (root == NULL)
continue;
if (visited)
path.emplace_back(root->val);
else
{
s.emplace(make_pair(root, true));
s.emplace(make_pair(root->right, false));
s.emplace(make_pair(root->left, false));
}
}
}
以上三种遍历实现代码行数一模一样,如同递归遍历一样,只有三行核心代码的先后顺序有区别。
解释下三种非递归遍历(以下图举例):
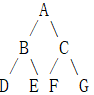
对二叉树而言,将每个框内结点集都看做一个局部,那么局部有 A,A B C,B D E,D,E,C F G,F,G 并且可以发现每个结点元素都是相邻的两个局部的重合结点。
算法流程:
1 每个结点元素都是相邻的两个局部的重合结点。对一个局部排好序后,通过取出一个重合结点过渡到与之相邻的局部进行新的局部排序。
2 用栈来保证局部顺序(排在前面的后入栈,排在后面的先入栈,保证局部元素出栈的顺序一定正确)
3 通过栈顶元素过渡到新局部的排序,对新局部的排序会导致该结点再次入栈,
4 当栈顶出现已完成过渡使命的结点时,就可以彻底出栈输出了,新栈顶元素会继续完成新局部的过渡
5 当所有结点都完成了过渡使命了,就全部出栈了。
参考: