二叉树相关

BST:

增：（插入）

　　　　 若当前的二叉查找树为空，则插入的元素为根节点，

　　　　 若插入的元素值小于根节点值，则将元素插入到左子树中，

　　　　 若插入的元素值不小于根节点值，则将元素插入到右子树中，

　　 递归上述过程，直到找到插入点为叶子节点

 

查：

给定一颗二叉查找树，查找某节点p的过程如下：

 将当前节点cur赋值为根节点root；

 若p的值小于当前节点cur的值，查找cur的左子树；

 若p的值不小于当前节点cur的值，查找cur的右子树；

 递归上述过程，直到cur的值等于p的值或者cur为空；

 当然，若节点是结构体，注意定义“小于”“不小于”“等于”的具体函数。

删： 450. Delete Node in a BST

记待删除的节点为p，分三种情况进行处理：

 p为叶子节点

　　p为叶子节点，直接删除该节点，再修改p的父节点的指针

 p为单支节点

　　若p为单支节点（即只有左子树或右子树），则将p的子树与p的父亲节点相连，删除p即可

 p的左子树和右子树均不空

　　若p的左子树和右子树均不空，则找到p的直接后继d(p的右孩子的最左子孙)，因为d一定没有左子树，所以使用删除单支节点的方法：

删除d，并让d的父亲节点dp成为d的右子树的父亲节点；同时，用d的值代替p的值；

　　对偶的，可以找到p的直接前驱x(p的左孩子的最右子孙)，x一定没有右子树，所以可以删除x，并让x的父亲节点成为x的左子树的父亲节点。

  

 二叉树树的遍历 递归or非递归

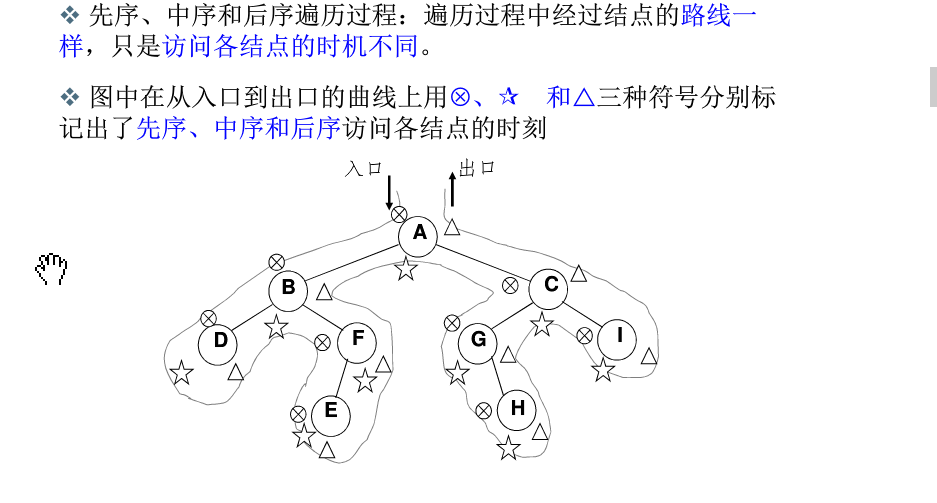
push是第一次访问

pop是第二次访问 

 

class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        Stack<TreeNode> s =  new Stack<TreeNode>();
        List<Integer> res = new ArrayList<Integer>();
        while(root!=null||!s.isEmpty()){
            while(root!=null){
                s.push(root);
                res.add(root.val);
                root = root.left;
            }
            if(!s.isEmpty()){
                root = s.pop();
                root = root.right;
            }
        }
        return res;
    }
}

class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        Stack<TreeNode> s =  new Stack<TreeNode>();
        List<Integer> res = new ArrayList<Integer>();
        while(root!=null||!s.isEmpty()){
            while(root!=null){
                s.push(root);
                res.add(0,root.val);
                root = root.right;
            }
            
            if(!s.isEmpty()){
                root = s.pop();
                root = root.left;
            }
        }
        return res;
    }
}

 

前序遍历  ： http://www.cnblogs.com/zle1992/p/8387902.html

中序遍历 ：http://www.cnblogs.com/zle1992/p/8342423.html

后序遍历 ：http://www.cnblogs.com/zle1992/p/8458643.html

根据前序中序，构造二叉树 http://www.cnblogs.com/zle1992/p/8360249.html

根据中序后序，构造二叉树 http://www.cnblogs.com/zle1992/p/8379513.html

 

层序遍历（利用queue）：http://www.cnblogs.com/zle1992/p/8350435.html

　　　　　　　　　　　　http://www.cnblogs.com/zle1992/p/8350511.html

　　　　　　　　　　　　http://www.cnblogs.com/zle1992/p/8398387.html

 

 

59按之字形顺序打印二叉树

60把二叉树打印成多行

 

 

二叉树相关：

　　　　61序列化二叉树

　　　　57二叉树的下一个结点

　　　　58对称的二叉树  101. Symmetric Tree（判断二叉树是否对称）　　

•  求路径和

  • 112. Path Sum  （判断路径和是否等于某值）  (路径是从root到叶子节点)
  • 113. Path Sum II（求等于某个数的所有路径）24二叉树中和为某一值的路径   (路径是从root到叶子节点)　　
  • 437. Path Sum III（路径可以任意点开始，任意点结束）
  • 129. Sum Root to Leaf Numbers（从根节点加到叶子节点的和）

 

• 最低公共祖先：

  • 236. Lowest Common Ancestor of a Binary Tree（最低公共祖先，难理解）
  • 235. Lowest Common Ancestor of a Binary Search Tree(LCA最低公共祖先)

 

平衡二叉树 Balanced Binary Tree（AVL树）

这个方案很好的解决了二叉查找树退化成链表的问题，把插入，查找，删除的时间复杂度最好情况和最坏情况都维持在O(logN)。