题目:戳这里
思路来源:视频讲解
题意:有n个箱子按1...n标号,每个箱子有大小为di的钻石概率为pi,我们初始有个大小为0的钻石,从1到n按顺序打开箱子,遇到比手中大的箱子就换,求交换次数的数学期望。
解题思路:这题跟上题[点这里]很像,都是找到一个子状态,利用数学期望的可加性,处理求和即可。这里的子状态为每一次交换的状态,即
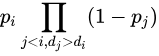
前j个比i大的概率积用树状数组维护。
附ac代码:

1 #include <cstdio> 2 #include <cstdlib> 3 #include <iostream> 4 #include <cstring> 5 #include <algorithm> 6 #include <cmath> 7 #include <queue> 8 #include <vector> 9 #include <string> 10 #include <map> 11 #include <set> 12 using namespace std; 13 typedef long long ll; 14 const ll mod = 998244353; 15 const int maxn = 1e5 + 10; 16 int n; 17 struct nod 18 { 19 int id; 20 ll d; 21 ll p; 22 }bx[maxn]; 23 bool cmp(nod a, nod b) 24 { 25 if(a.d > b.d) return 1; 26 else if(a.d == b.d && a.id < b.id) return 1; 27 return 0; 28 } 29 ll pmul(ll a, ll b) 30 { 31 ll res = 0; 32 while(b) 33 { 34 if(b&1) 35 res = (res + a) % mod; 36 b >>= 1; 37 a = (a + a) % mod; 38 } 39 return res; 40 } 41 ll pmod(ll a, ll b) 42 { 43 ll res = 1; 44 while(b) 45 { 46 if(b&1) 47 res = pmul(res, a) % mod; 48 b >>= 1; 49 a = pmul(a, a) % mod; 50 } 51 return res; 52 } 53 ll exgcd(ll a, ll b, ll &x, ll &y) 54 { 55 if(a == 0 && b == 0) return -1; 56 if(b == 0) 57 { 58 x = 1;y = 0; 59 return a; 60 } 61 ll d = exgcd(b, a % b, y, x); 62 y -= a/b*x; 63 return d; 64 } 65 ll mod_rev(ll a, ll n) 66 { 67 ll x, y; 68 ll d = exgcd(a, n, x, y); 69 if(d == 1) return (x % n + n) % n; 70 else return -1; 71 } 72 int lowbit(int x) 73 { 74 return x&(-x); 75 } 76 ll c[maxn * 4]; 77 ll getm(int i) 78 { 79 ll s = 1; 80 while(i > 0) 81 { 82 s = pmul(s , c[i]) % mod; 83 i -= lowbit(i); 84 } 85 return s; 86 } 87 void add(int i, ll val) 88 { 89 while(i <= n) 90 { 91 c[i] = pmul(c[i], val) %mod; 92 i += lowbit(i); 93 } 94 } 95 int main() 96 { 97 98 ll inv = mod_rev(100ll, mod); 99 // printf("%lld ", inv); 100 scanf("%d", &n); 101 for(int i = 0; i < maxn; ++i) 102 c[i] = 1; 103 for(int i = 1; i <= n; ++i) 104 { 105 scanf("%lld %lld", &bx[i].p, &bx[i].d); 106 bx[i].id = i; 107 } 108 sort(bx + 1, bx + 1 + n, cmp); 109 110 ll ans = 0; 111 for(int i = 1; i <= n; ++i) 112 { 113 // printf("%lld ", getm(bx[i].id)); 114 //printf("%lld %lld %d ", bx[i].p, bx[i].d, bx[i].id); 115 ans = (ans + getm(bx[i].id) * bx[i].p % mod * inv % mod) % mod; 116 add(bx[i].id, ((100 - bx[i].p) * inv) % mod); 117 } 118 printf("%lld ", ans); 119 }
