POJ 1375 Intervals 计算几何基础

题意：

题目链接
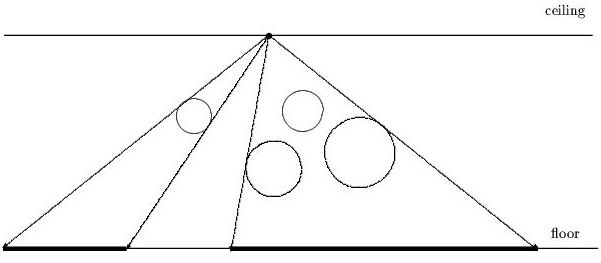
给你一个点光源，一些不透明的管子（圆），求每一段阴影部分的左右区间 管子个数<=500

思路：

其实就是点光源作圆的切线
圆的阴影投影到地板上后，再按左端点排序合并就行了

注意事项：

要注意精度
求切线1.0版本：

inline point rot(point pt,double sn,double cs)
{
	point _pt;
	_pt.x=pt.x*cs-pt.y*sn,_pt.y=pt.y*cs+pt.x*sn;
	return _pt;
}

double d=dis(st,o);
double sn=r/d,cs=sqrt(1-sn*sn);
point p=rot(o-st,sn,cs);
a[++cnt].rr=inc(st,st+p);
p=rot(o-st,-sn,cs);
a[cnt].ll=inc(st,st+p);

Wrong Answer

求切线2.0版本：

double d=dis(st,o);
sn1=r/d;dg1=asin(sn1);
sn2=(st.x-o.x)/d;dg2=asin(sn2);
a[++cnt].ll=st.x-st.y*tan(dg1+dg2);
a[cnt].rr=st.x-st.y*tan(dg2-dg1);

稳稳Accepted
据说是因为sqrt精度太低。。

code：

#include<cstdio>
#include<cmath>
#include<algorithm>
#include<iostream>
using namespace std;
const int N=505;
const double eps=1e-7;
int n;
double sn1,sn2,dg1,dg2;
struct sec{double ll,rr;}a[N];
bool operator<(sec x,sec y){return x.ll<y.ll;}
struct point{double x,y;}st;
const point e1=(point){-100,0},e2=(point){100,0};
point operator+(point x,point y){return (point){x.x+y.x,x.y+y.y};}
point operator-(point x,point y){return (point){x.x-y.x,x.y-y.y};}
double operator^(point x,point y){return x.x*y.y-x.y*y.x;}
inline double dis(point x,point y)
{
	return sqrt((x.x-y.x)*(x.x-y.x)+(x.y-y.y)*(x.y-y.y));
}
inline double inc(point p1,point p2)
{
	double s1=(e1-p1)^(e2-p1),s2=(e2-p2)^(e1-p2);
	return p2.x+(p1.x-p2.x)*s2/(s1+s2);
}
int main()
{
	while(7)
	{
		scanf("%d",&n);
		if(!n) break;
		scanf("%lf%lf",&st.x,&st.y);
		int cnt=0;
		for(int i=1;i<=n;++i)
		{
			double r=0;point o;
			scanf("%lf%lf%lf",&o.x,&o.y,&r);
			if(r<eps)continue;
			double d=dis(st,o);
			sn1=r/d;dg1=asin(sn1);
            sn2=(st.x-o.x)/d;dg2=asin(sn2);
            a[++cnt].ll=st.x-st.y*tan(dg1+dg2);
            a[cnt].rr=st.x-st.y*tan(dg2-dg1);
		}
		sort(a+1,a+cnt+1);
		double ll=a[1].ll,rr=a[1].rr;
		for(int i=2;i<=cnt;++i)
		{
			if(rr<a[i].ll)
			{
				printf("%.2f %.2f
",ll,rr);
				ll=a[i].ll,rr=a[i].rr;
			}
			else rr=max(rr,a[i].rr);
		}
		printf("%.2f %.2f
",ll,rr);
		puts("");
	}
	return 0;
}